
3. Crittografia visuale per immagini in toni di grigio
Fino ad adesso si è supposto che il segreto S consistesse
in un'immagine costituita da soli due colori, il bianco ed il nero. In questo
capitolo si presenterà uno schema per immagini in toni di grigio nel
quale l'immagine originale consiste di un certo numero g di toni di
grigio.
Si noti che l'immagine ricostruita, come le share, è formata sempre e solo
da pixel bianchi e neri: è la loro composizione a generare zone che appaiono,
all'occhio umano, come zone colorate da diverse sfumature di grigio.
Per iniziare si presenta un esempio analogo a quello dello schema (2,2), con m=4, visto in Figura 7, riadattato, però, per la codifica di 3 toni di grigio (che, per semplicità, indicheremo con bianco, nero e grigio).
In tale esempio un pixel bianco veniva codificato con 2 sottopixel neri e 2 bianchi; il pixel nero, invece, con 4 sottopixel neri. Un riadattamento funzionante può essere quello che non modifica la rappresentazione dei pixel bianchi e neri e che codifica un pixel grigio con tre sottopixel neri ed uno bianco.

Figura 12 - Schema (2,2) con m=4 riadattato per la codifica di 3 toni di grigio
Come si può notare dalla figura, ogni
pixel nelle due share è rappresentato sempre da due sottopixel bianchi
e due neri, indipendentemente dal colore del pixel originale, benché
la loro composizione generi, per ogni pixel, 2,3 o 4 pixel neri a seconda del
valore del pixel originale.
La figura contiene una sola codifica per ogni tono di grigio. In realtà,
ogni tono è rappresentato da una matrice di base: le permutazioni delle
colonne di tali matrici generano tutte le possibili codifiche dei corrispondenti
toni di grigio.
Osservando la Figura 13, si può notare come questa semplice modifica al VCS a due toni ci permetta di codificare un immagine a 3 toni senza perdere in sicurezza. La figura infatti mostra una immagine in cui i 3 toni di grigio sono chiaramente distinguibili; le due share, invece, sono codificate in modo che i colori non siano distinguibili affatto. Ovviamente, solo con la sovrapposizione delle share si riesce a ricostruire l'immagine originale.
Figura 13 - Immagine in 3 toni di grigio
É possibile generalizzare tale problema alla codifica di un'immagine con un numero arbitrario di sfumature di grigio. Lo schema che permette tale codifica è chiamato g-GVCS (Gray Visual Cryptography Scheme a g toni).
Si utilizzeranno i seguenti parametri:
Affinché lo schema sia corretto è necessario che valgano le seguenti proprietà:
Naturalmente è possibile generare un g-GVCS anche che per strutture di accesso con insiemi qualificati ed insiemi proibiti. In tal caso, le proprietà di cui dovrà godere tale schema sono analoghe a quelle viste per la struttura di accesso per VCS a due colori e sono le seguenti:
Si presenta ora una tecnica per la costruzione di una struttura di accesso per la codifica di un'immagine con g toni di grigio. Per far ciò, si parte da una struttura di accesso per immagini in bianco e nero ad espansione m.
Di tale VCS si considerano le matrici di base S0 ed S1, di dimensione n x m, allo scopo di costruire G0, G1, ..., Gg-1, matrici di base, di dimensione n x (g-1)·m, della struttura di accesso a g toni di grigio. La costruzione della generica matrice Gi è definita come segue:
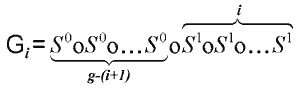
dove il simbolo o indica l'operazione di concatenazione.
Per maggior chiarezza si osservi anche la Figura 14 che mostra un esempio di un g-GVCS(2,4) con m=2, g=4 ed insieme dei qualificati Q={ {1,2}, {2,3}, {1,2,3} } (F è formato dai restanti insiemi). É facile verificare che la sovrapposizione delle share di un insieme qualificato, genera 4 diversi toni di grigio, mentre le singole share (come la sovrapposizione delle share di un insieme non qualificato) non forniscono alcuna informazione sull'immagine originale, in quanto ogni tono è rappresentato da 3 sottopixel neri e 3 sottopixel bianchi.
Figura 14 - Esempio di un 4-GVCS costruito a partire da uno schema in bianco e nero