Punti di rottura

Abbiamo descritto un algoritmo di greedy che cerca di massimizzare prefix(π) in ogni passaggio, ma ogni giocatore di scacchi sa che greedy conduce spesso alla decisione sbagliata. I buoni giocatori di scacchi usano una nozione più sofisticata di greedy che valuta una posizione basandosi su molti fattori sotterranei piuttosto che semplicemente sul valore superficiale di un pezzo che possono prendere.

Il problema connesso all’SRS è che il prefix(π) è una misura ingenua del nostro progresso verso l’identity permutation, e non riflette accuratamente quanto sia difficile ordinare una permutazione. Più sotto definiamo breakpoints (punti di rottura) quelli che possono essere visti come “colli di bottiglia” nell’ordinamento da inversione. Usare il numero di breakpoints, piuttosto che il prefix(π), come base di greed conduce ad un algoritmo migliore per l’ordinamento da inversione, nel senso che produce una soluzione più vicina all’ottimale. Prima di andare oltre è importante definire che cosa sono le adiacenze e i breakpoints.

Data la permutazione π = π₁ π₂ π₃ . . . π_n-1 π_{n ,} una coppia di elementi π _i e π _{i + 1} sono adiacenti se π _i+1 = π _i + 1.

Ad esempio se π = 1 9 3 4 7 8 2 6 5 allora (3, 4) oppure (7, 8) e (6,5) sono coppie adiacenti.

Esempio: 

C’è un punto di rottura fra ciascun elemento adiacente e non consecutivo :

π = 1 9 3 4 7 8 2 6 5

in questo caso le coppie (1,9), (9,3), (4,7), (8,2) e (2,6) costituiscono punti di rottura di permutazione π e b(π) è il numero di punti di rottura nella permutazione π. In poche parole si definisce adiacenza, un paio di elementi adiacenti che sono consecutivi e breakpoint, un paio di elementi adiacenti che sono non consecutivi:

π = 5 6 2 1 3 4 → estende π con π₀ = 0 e π₇ = 7

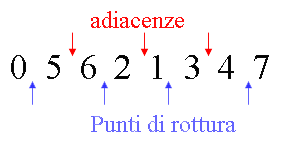
Fig.6 Punti di adiacenza (5,6) (2,1) (3,4) e di rottura (0,5) (6,2) (1,3) (4,7).

Una permutazione di n elementi può avere tanti breakpoints pari a n+1 e tanto pochi come 0 (l’identity permutation 0 1 2 3 4 5 6 7 8).

Ogni breakpoint corrisponde ad un paio di elementi π_i e π_i+1 che sono vicini in π ma non nella identity permutation. Infatti l’identity permutation è l’unica che non presenta breakpoints. Comunque gli elementi non consecutivi π_i e π_i+1 che formano un breakpoint devono essere separati nel processo che porta alla trasformazione di π nell’identity, e possiamo dunque vedere l’ordinamento attraverso le inversioni come il processo di eliminazione dei breakpoints. L’osservazione che ogni inversione può eliminare al massimo 2 breakpoints (uno alla fine a sinistra e l’altro alla fine a destra dell’inversione) implica immediatamente che d(π) > b(π)/2, dove b(π) è il numero di breakpoints in π.