Problema della decodifica: algoritmo di Viterbi

L'algoritmo fu originariamente concepito per la trasmissione dati nello spazio, ove bisogna tener conto di condizioni avverse che possono produrre variazioni aleatorie del segnale trasmesso. Questo problema viene normalmente affrontato adoperando codici che introducono una opportuna ridondanza per proteggerli dagli errori. Una classe importante è costituita dai codici a convoluzione, nei quali i dati originali vengono trasformati e in un certo senso ripetuti tramite una opportuna operazione matematica. Infatti, mentre nei codici cosiddetti a blocco si applica la stessa codifica ai singoli blocchi in cui il flusso di dati viene partizionato, nei codici a convoluzione la codifica intreccia porzioni di blocchi dell'originario flusso di dati e ogni simbolo partecipa alla determinazione di simboli di codice un elevato numero di volte. Poiché la codifica a convoluzione rende il flusso di dati particolarmente interdipendente, la decodifica richiede calcoli molto più complessi di quanto sia necessario in una codifica a blocchi disgiunti. È qui che interviene l'algoritmo di Viterbi per determinare quale sequenza di dati trasmessi sia la più probabile causa del flusso osservabile in uscita. L'algoritmo calcola la probabilità dei diversi flussi in ingresso in modo ricorsivo, eliminando in blocco, ad ogni passo, quelli di probabilità minore. Tale eliminazione permette una cospicua riduzione della complessità delle relative operazioni di calcolo.

Il modello stocastico cui si applica l'algoritmo di Viterbi è sufficientemente generale da adeguarsi alla descrizione di fenomeni di diversissimo genere. In conseguenza, man mano che lo sviluppo scientifico-tecnologico lo permetteva, l'uso dell'algoritmo si è esteso a molti altri campi, dove il fenomeno studiato è modellato tramite una cosiddetta catena nascosta di Markov che potremmo caratterizzare come una catena di Markov osservata attraverso un canale disturbato nel senso di Shannon. In particolare, la biologia computazionale, la linguistica computazionale ed il riconoscimento vocale sono fra i campi di applicazione dell'algoritmo oggi di maggiore attualità.

Vediamo ora più in dettaglio come funziona l'Algoritmo di Viterbi. Innanzi tutto bisogna spiegare meglio cos'è un codice convoluzionale; la convoluzione è un'operazione matematica che sparpaglia il contenuto di un segnale secondo l'andamento di un altro, in pratica uno schema generale di un codificatore a convoluzione è rappresentato in figura 1.


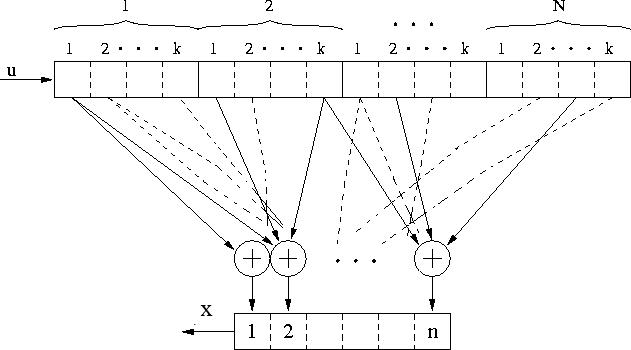
Figura 1 - Schema generico di codificatore convoluzionale

Qui u rappresenta il flusso di dati in ingresso e X il flusso codificato, vengono letti k bit in ingresso ed entrano in un registro a scorrimento, una funzione combinatoria genera quindi n bit in uscita, che vengono poi trasmessi e subiscono in genere un certo processo di deterioramento.

L'algoritmo di Viterbi è il modo ottimo di decodifica, nel senso del criterio della massima verosimiglianza, ed è anche molto efficiente.

Uno schema del tipo di figura 1 può essere rappresentato anche come diagramma a stati, dove:

• il numero di stati è pari a ;
• il numero di transizioni da ogni stato è ;
• le transizioni da uno stato all'altro possono essere etichettate dal blocco di bit in uscita (per quello stato).

Ad esempio un diagramma per un codificatore con k =1 (un bit per volta entra nel registro), N =2 (registro a due locazioni) e n =3 (tre bit per volta in uscita) genera un diagramma degli stati del tipo di figura 2 (i rami del grafo e le relative etichette sono scelte dalla particolare funzione combinatoria implementata).

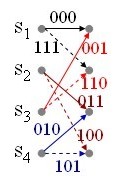
Figura 2 - Diagramma a stati di un codificatore convoluzionale con k =1; N =2, n =3.

Un modo per rappresentare dinamicamente il flusso di dati di un codificatore convoluzionale, molto utile per la decodifica con l'algoritmo di Viterbi, è il cosiddetto diagramma a traliccio: per ogni istante di tempo dall'inizio alla fine della ricezione vengono disegnati tutti gli stati possibili del codificatore; partendo dallo stato di reset si possono disegnare tutte le transizioni come cammini nel traliccio. Bisogna introdurre una metrica, cioè una distanza tra le transizioni tra gli stati e la sequenza di simboli ricevuta, ad esempio la distanza di Hamming, che si ottiene semplicemente contando il numero di bit errati.

Qui interviene l'algoritmo di Viterbi che opera iterativamente, alla ricezione di ogni simbolo (di n bit), valutando la distanza di al massimo s percorsi (sopravvissuti) e limitando quindi notevolmente la complessità di calcolo che sarebbe s L con L lunghezza della sequenza. L'animazione in figura 3 mostra il calcolo passo passo della distanza di ogni percorso nel traliccio e la scelta dei percorsi sopravvissuti fino alla fine della sequenza, dove il percorso con minore distanza indica la sequenza corretta.

La sequenza ricevuta è 110 111 011 001 000 000 000, la sequenza corretta è 000 111 011 001 000 000 000, e ha corretto un doppio errore nel primo simbolo.

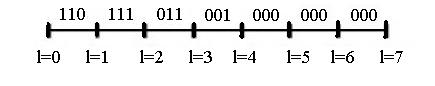
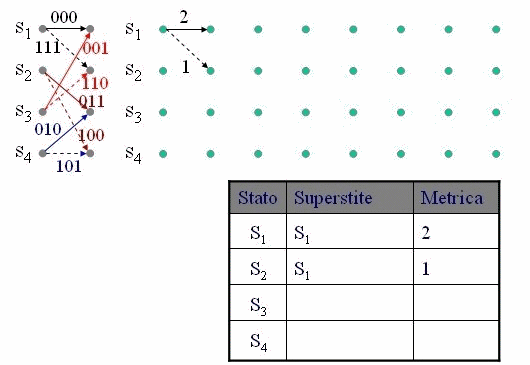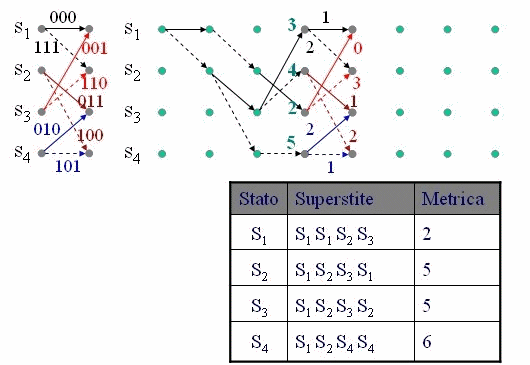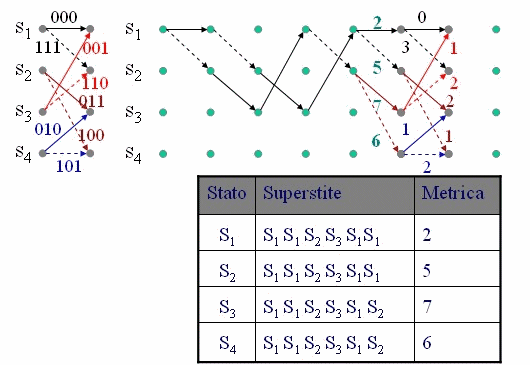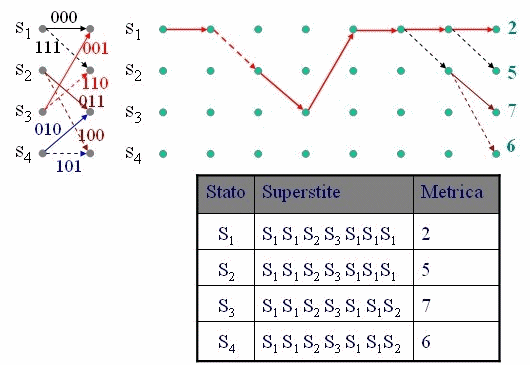
Figura 3 - Esempio di applicazione dell'algoritmo di Viterbi