Per descrivere quali siano le principali tecniche informatiche che ci permettono di riconoscere un pattern di lunghezza fissata, ripetuto più volte all'interno di una sequenza, anche qualora le ripetizioni siano soggette a mutazione, ci aiuteremo attraverso un piccolo esempio. Supponiamo di generare in maniera random t=5 sequenze di n=30 nucleotidi del DNA
e di impiantare al loro interno un pattern segreto P = ATGCAAC di lunghezza l = 7.
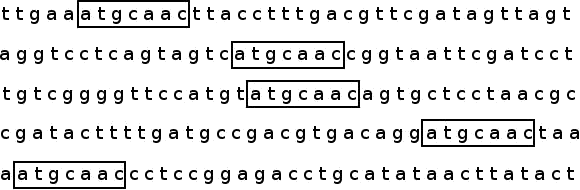
Supponiamo in fine, di non sapere la posizione dei pattern impiantati, ma di conoscerne la lunghezza.
A partire da queste conoscenze possiamo ricostruire P semplicemente contando il numero di occorrenze di ogni possibile stringa di lunghezza l presente all'interno delle nostre sequenze.
Attraverso una semplice analisi statistica infatti, risulta evidente che, essendo le sequenze composte da soli t * (n + l) = 5 * (30 + 7) = 185 nucleotidi, è improbabile che un pattern diverso da quello impiantato vi si ripeta più di una volta; pertanto, il pattern sovrarappresentato, generalmente, coincide proprio con il pattern che stiamo cercando.
Purtroppo, da un punto di vista biologico le sequenze di pattern ripetuti sono soggette a mutazioni genetiche frequenti che alterano il motivo regolatore
Osservando tali mutazioni, rappresentate nella figura dai caratteri maiuscoli, è evidente che ricostruire il pattern diventa più complicato poiché la stringa ricercata non si ripete in modo identico, ma ogni ripetizione presenta una certa variazione rispetto alle altre. Non è più possibile descrivere il motivo in modo univoco, viene così introdotta una rappresentazione più flessibile detta stringa di consenso o consensus per costruire la quale si fa ricorso alle matrici di profilo.
Consideriamo ancora le nostre t=5 sequenze del DNA, composte da n=30 nucleotidi, ed un array 
con
.
A partire dalla posizione 
, estraiamo un pattern di lunghezza l (dimensione del motivo cercato) da ognuna delle t sequenze formando una matrice t x l, detta matrice di allineamento, il cui elemento (i, j) è il nucleotide di posizione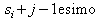
nella i-esima sequenza.
In figura vengono evidenziati tra parentesi i pattern estraibili dalle sequenze del nostro esempio partendo dall'array di posizioni s=(6, 16, 17, 28, 2) e la relativa matrice di allineamento:
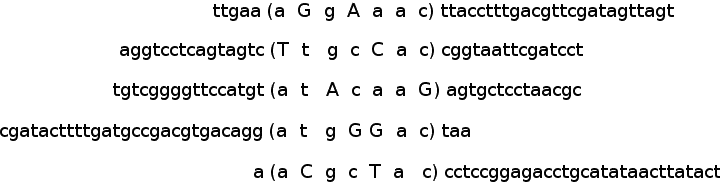
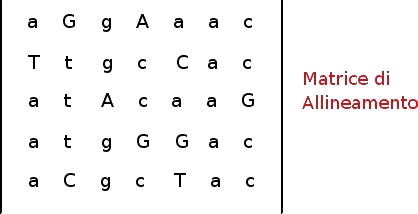
Attraverso la matrice di allineamento possiamo calcolare la matrice di profilo 4 x l, dove 4 indica il numero di nucleotidi presenti all'interno del DNA.
L'elemento (i, j) della profile matrix conta il numero di occorrenze del nucleotide i-esimo nella colonna j-esima della matrice di allineamento.
I nucleotidi con occorrenza maggiore diventano elementi della consensus string.
Chiaramente, esiste la possibilità che in una qualche colonna della matrice di profilo il massimo sia condiviso da due o più nucleotidi;in tal caso, una stessa matrice produrrebbe due o più consensus. Tale evenienza sembrerebbe generare una ambiguità nel matching con il motivo cercato. Tuttavia, essendo il motivo reale soggetto a mutazioni, non possiamo aspettarci che la Consensus String vi coincida perfettamente. Verranno invece considerate consensus di un particolare motivo tutte le stringhe che differiscono da questo di al più un certo numero massimo di caratteri. In generale infatti, sarà sufficiente che la distanza tra una consensus e il motivo rappresentato risulti minore della distanza tra due motivi differenti. In seguito, comunque, vedremo che l'algoritmo proposto tende a ridurre le possibilità che ci si trovi di fronte ad una matrice con tale caratteristica.
Ritornando al nostro esempio, osserviamo che al variare di s è possibile costruire nuove matrici di profilo. A questo punto, abbiamo bisogno di definire un metodo di comparazione tra le diverse profiles ottenute; per farlo, denotiamo con P(s) la matrice di profilo relativa alla generica stringa degli indici s e con 
il massimo nella colonna j-esima di P(s).
Possiamo definire per ogni s un consensus score:
Il massimo Score(s, DNA) possibile è dato dal prodotto l x t, ottenibile nel caso in cui le righe della matrice di allineamento siano tutte identiche tra loro. Il minimo Score(s, DNA) invece, corrisponde ad (l * t) /4 e si ottiene nel caso in cui ognuno dei nucleotidi è presente con la stessa frequenza all'interno delle colonne della matrice di allineamento.
Attraverso questa nuova definizione possiamo formulare il problema della ricerca dei motivi come ricerca della stringa degli indici s che massimizza lo Score(s, DNA).
Input: una matrice t x n di sequenze di DNA,ed un intero l rappresentante la lunghezza del motivo da cercare.
Output: un array s di t indici che massimizza lo Score(s, DNA).
L’approccio di forza bruta per risolvere tale problema scandisce tutte le possibili soluzioni al fine di trovarne la migliore.
RicercaMassimoScore(DNA, t, n, l)
1 massimoScore <- 0
2 for each 
from (1,1 . . . 1) to (n-l+1, . . ., n-l+1)
3 if (Score(s, DNA) > massimoScore)
4 massimoScore <- Score(s, DNA)
5 migliorMotivo <- s
6 return migliorMotivo
possibili combinazioni di s, la complessità totale dell’algoritmo è valutata come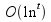 
.
Questo stesso problema può anche essere riformulato come problema di ricerca di una stringa mediana. Per farlo, definiamo la distanza di Hamming tra due stringhe di lunghezza l, come il numero di posizioni (nucleotidi) che differiscono all'interno delle due stringhe.
Per esempio, date due stringhe u = GATAAGTC e v = GCTAACTC,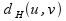
= 2
Supponiamo che sia un array di indici di partenza e sia v una generica stringa di lunghezza l; possiamo definire la distanza di Hamming totale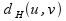 tra v ed s come:
dove 
è la distanza di Hamming tra v e la stringa presa a partire dall’indice nella i-esima sequenza di DNA.
Useremo 
per denotare la più piccola distanza di Hamming totale tra una data stringa v e un qualsiasi insieme di posizioni iniziali s nel DNA. Trovare tale distanza è un problema semplice: per prima cosa bisogna trovare il miglior match per v nella prima sequenza di DNA, poi il miglior match nella seconda sequenza, e così via. A questo punto utilizziamo i valori di matching ottenuti per calcolare la distanza totale di Hamming. Tale distanza coinciderà in particolare con la più piccola distanza totale di Hamming di v sul DNA. Occorre ripetere questa operazione per tutte le 
possibili v di lunghezza l.
Definiamo infine la stringa mediana per il DNA come la stringa v che minimizza la TotalDistance(v,DNA).
Formuliamo il problema della ricerca di una stringa mediana nelle sequenze di DNA come segue:
Problema di ricerca della Stringa Mediana :
Input: Una matrice t x n di sequenze di DNA e l, cioè la lunghezza del pattern da ricercare.
Output: Una stringa v di l nucleotidi che minimizza TotalDistance(v,DNA) su tutte le stringhe di tale lunghezza.
Applicando la tecnica della forza bruta per risolvere tale problema, arriviamo al seguente algoritmo:
RicercaStringaMediana(DNA,t,n,l)
1 migliorStringa <- AAA…A
2 migliorDistanza <- 8
3 for each s from AAA…A to TTT…T
4 if TotalDistance(s,DNA) < migliorDistanza
5 migliorDistanza <- TotalDistance(s,DNA)
6 migliorStringa <- s
7 return migliorStringa
Tale algoritmo considera ognuna delle stringhe di nucleotidi di lunghezza l e ad ogni passo calcola la TotalDistance. Poiché data una qualunque stringa s, possiamo calcolarne la TotalDistance(s,DNA) in tempo O(nt), il tempo di esecuzione totale dell'algoritmo sarà
Sebbene il problema della Stringa Mediana sia un problema di minimizzazione e quello della Ricerca dei Motivi un problema di massimizzazione, essi rappresentano soluzioni equivalenti.
In particolare, minimizzare la TotalDistance equivale a massimizzare lo Score(s, DNA).
Sia infatti s un insieme di posizioni iniziali, Score(s, DNA) il suo score e sia w la stringa di consenso del profilo corrispondente. Abbiamo che:
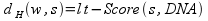
Pertanto, essendo lt costante, una minimizzazione della distanza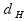
può essere ottenuta massimizzando Score(s, DNA) su tutte le scelte di s.