4. Algotmi Lossless

4.1 L'algoritmo di Huffman

Consideriamo un libro scritto in italiano, sicuramente ci sarà un'alta frequenza nell'uso della lettera a e una bassa della z. Si potrebbe perciò pensare di comprimere il testo usando codici binari molto brevi per la a e più lunghi per la z. L'algoritmo di Huffman [2] analizza le frequenze dei simboli da comprimere, sostituendo un codice, tipicamente ad 8 bit, con una sequenza più corta di bit (minimo 1), in funzione della frequenza del dato da comprimere.

Un indagine statistica è alla base dell'algoritmo di Huffman per la compressione dei dati. I passi sostanziali dell'algoritmo sono i seguenti:

1. si esaminano i dati da comprimere per verificare la frequenza dei vari caratteri;
2. si crea un codice pre-fisso ottimo;
   1. si raggruppano i simboli in ordine di occorrenza
   2. si combinano i due simboli con occorrenza minore, creando un nuovo nodo (che avrà occorrenza pari alla somma delle occorrenze dei due) e mettendoli come figli
   3. si ripete il processo fino a non aver ottenuto un albero
3. si sostituiscono le stringhe di bit che rappresentano i caratteri con i corrispettivi;
4. si salva il file aggiungendo (come intestazione) il codice calcolato.

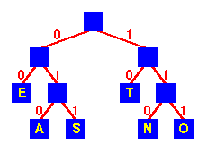
Il codice che si crea viene detto pre-fisso in quanto nessuna delle stringhe di bit risulta essere prefisso di un'altra (ad esempio 11 non è prefisso di 1001), in questo modo non è necessario inserire dei marcatori tra un codice e l'altro. Inoltre è ottimo, poiché minimizza la lunghezza dei codici. Un esempio di applicazione dell'algoritmo di Huffman è presentato in Figura 5. Per una data distribuzione di frequenze ci possono essere diversi codici di Huffman; però ognuno di essi restituisce un codice ottimo (tutti danno la stessa compressione).

STRINGA CODIFICA TEA 10 00 010 SEA 011 00 010 TEN 10 00 110

Figura 5

Un file compresso con l'algoritmo di Huffman è ottimo quando le frequenze dei suoi caratteri sono fortemente sbilanciate, mentre il caso peggiore si rivela quando un carattere ha probabilità 1/2 di trovarsi nel testo. L'algoritmo di creazione del codice, risulta migliore quando invece le frequenze dei caratteri sono potenze intere di 1/2 (altrimenti, il codice ottenuto potrebbe non essere eccessivamente buono).

4.2 Algoritmi LZ

La famiglia degli algoritmi di LZ [3], sebbene ha molte varianti, è basata essenzialmente sulla sostituzione di testo. Essa ha il vantaggio di comprimere in modo semplice ed efficiente tipi di dati eterogenei, come testo, immagini, database, ecc.. La sua caratteristica principale è che non richiede informazioni a priori sui dati, inoltre le statistiche sul file da comprimere sono acquisite implicitamente durante la fase di codifica.

Il processo di codifica analizza il file tenendo conto di due parametri, la posizione e la lunghezza di una frase già incontrata, ed ogni volta che viene trovato un elemento di questo tipo lo sostituisce effettuando così una compressione del file. Questi schemi possono essere resi ulteriormente più efficaci numerando il testo di input modulo N, dove N è l'effettiva lunghezza della finestra, creando così un buffer circolare.
Possiamo inoltre dare una ulteriore suddivisione di questo tipo di algoritmi considerandone due principali gruppi.
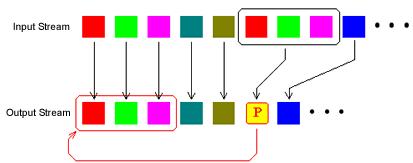
I metodi del primo gruppo cercano di verificare se la sequenza di caratteri che è stata appena compressa è già occorsa precedentemente e, invece di ripeterla, la sostituiscono con il puntatore alla precedente occorrenza , come si nota dalla figura 6. Qui il dizionario è rappresentato dai dati precedentemente processati. Tutti i metodi di questo gruppo sono basati sull'algoritmo LZ77. Un raffinamento di questo algoritmo è  LZSS, algoritmo sviluppato nel 1982 da Storer e Szymanski.

Figura 6

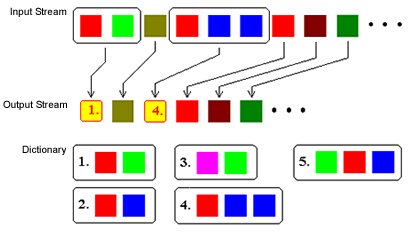
Gli algoritmi del secondo gruppo creano un dizionario delle frasi già occorse nei dati in input. Quando viene incontrata una frase già presente nel dizionario, viene restituito il numero che indicizza la frase nel dizionario (vedi figura 7).Questi metodi sono basati sull'algoritmo LZ78 e sui suoi successivi raffinamenti come ad esempio il metodo LZW, che fu sviluppato da Terry Welch nel 1984.

Figura 7

Infine, alcune varianti dello schema di Lempel Ziv aplicano un'ulteriore compressione all'output, come ad esempio la codifica di Huffman (LZH). Si è inoltre avuta una soluzione ibrida tra LZ77 e LZ78 chiamata LZFG. Quindi, ogni variante dell'algoritmo, differisce dalle altre sostanzilmente solo per pochi dettagli. Successivamente saranno introdotte alcune varianti dell'algoritmo di Lempel-Ziv, un'introduzione a tali varianti è presentata nella seguente Tabella.

4.2.1 LZ77

L'algoritmo Lempel-Ziv 77 (LZ77) [4] è il primo algoritmo di compressione di Lempel-Ziv. Il dizionario è creato a partire dalla sequenza precedentemente codificata. Per ottenere la codifica si esamina la sequenza in input tramite una window. La finestra consiste di due parti:

• un search buffer che contiene una parte della sequenza recentemente codificata
• un look-ahead buffer che contiene la prossima porzione della sequenza che deve essere codificata.

Figura 8

L'algoritmo cerca, ad ogni passo, nella sequenza di caratteri una sottostringa che è già stata incontrata, se tale sequenza esiste viene compressa mediante un puntatore alla precedente occorrenza. In questo modo, più il file contiene elementi ripetuti, più la compressione è efficace. In un file di testo, ad esempio, se si incontra una ripetizione di una parola, la seconda viene sostituita con l'indirizzo della prima. La compressione massima raggiungibile è di 2,8 ad 1.

L' algoritmo di codifica

1. Fissa la posizione di codifica all'inizio del flusso in input;
2. trova il più lungo match nel lookahead buffer
3. restituisce la coppia (P,C), dove:
   • Pè il puntatore al match nella finestra;
   • C è il primo carattere nel lookahead buffer di cui non si è riusciti a fare match;
4. se il lookahead buffer non è vuoto
         sposta la posizione di codifica (e la finestra) di L+1caratteri in avanti e ritorna al passo 2.

L'algoritmo [5] potrebbe restituire anche semplicemente il puntatore al match, ma è possibile che non sia trovato nessun carattere che faccia match, in questo caso è necessario restituire qualche altra informazione. LZ77 risolve il problema restituendo oltre al puntatore il primo caratterenel lookahead buffer dopo il match. Se non c'è match, l'output è costituito da un puntatore nullo e il carattere che si trova nella posizione di codifica.

Per quanto riguarda la decodifica la gestione della finestra è la stessa della codifica. Inoltre in ogni passo l'algoritmo prende in input una coppia (P,C) e restituisce la sequenza della finestra specificata da P e dal carattere C. Il rapporto di compressione di questo metodo è molto buono per molti tipi di dati, ma la codifica può essere abbastanza lunga, poichè ci sono molti confronti da effettuare tra il lookahead buffer e la window. D'altro canto, la decodifica è molto semplice e veloce. Viene usata poca memoria sia per la codifica che per la decodifica, in quanto la sola struttura tenuta in memoria è la window.

  4.2.2 LZSS

L'algoritmo derivato da LZ77 piu' comunemente usato è LZSS, formulato da James Storer e Thomas Szymanski nel 1982. Come abbiamo visto l' algoritmo LZ77 nel caso in cui non vengono trovati match nella window ritorna in output un carattere dopo ogni puntatore. Questa soluzione contiene però delle ridondanze, cioè o sarà ridondante il puntatore nullo o il carattere che potrebbe essere incluso nel prossimo match. L'algoritmo LZSS risolve questo problema in modo più efficiente, il puntatore è restituito solo se punta a un match più lungo del puntatore stesso, altrimenti sono restituiti dei caratteri. Poichè ora l'output conterrà sia caratteri che puntatori, bisognerà aggiungere ad ognuno un bit extra che ci permetterà di distinguere tra loro.

L'algoritmo di codifica

1. si fissa la posizione di codifica all'inizio del flusso in input;
2. si trova il più lungo match nella finestra per il lookahead buffer;
• P è il puntatore al match;
• L è la lunghezza del match;
3. se L >= lunghezza minima
         si restituisce P e si spostata la posizione di codifica in avanti di L caratteri;
   altrimenti
         è restituito il primo carattere del lookahead buffer e spostata la posizione di codifica in avanti di un carattere;
   
4. se ci sono più caratteri in input si ritorna al passo 2.

Questo algoritmo generalmente ottiene un migliore rapporto di compressione di LZ77 e fa lo stesso uso sia di capacità di calcolo che di memoria. La decodifica è ancora estremamete semplice e veloce tanto da farlo diventare la base per tutti i successivi algoritmi di questo tipo Infatti, è implementato in quasi tutti i programmi di compressione, come in PKZip, ARJ ecc.. Naturalmente, in ognuno è implementato con piccole differenze, come la lunghezza del puntatore (che può essere variabile), la taglia della finestra, il modo in cui è spostata (alcune implementazioni spostano la finestra con passi di N-caratteri) e così via.

  4.2.3 LZ78

L'algoritmo LZ78 [6] viene sviluppato a partire da LZ77 per eliminarne i problemi incontrati nel sua fase di sviluppo. Mentre in LZ77 il dizionario era definito da una window di lunghezza fissa riferita al testo precedentemente analizzato, in LZ78 viene abbandonato il concetto di windows. Inoltre in LZ78 il dizionario diventa una collezione potenzialmente illimitata di frasi precedentemente analizzate. LZ78 inserisce le frasi in un dizionario e, quando viene trovata un occorrenza ripetuta, viene restituito un token, che consiste nell'indice del dizionario, invece della frase stessa, e il carattere che segue la frase. A differenza di LZ77,non c'è necessità di passare la lunghezza della frase come parametro perchè nella fase di decodifica questa informazione è già conosciuta.

L' algoritmo di codifica

1. All'inizio, il dizionario e P sono vuoti;
2. C:= prossimo carattere nella sequenza da comprimere;
3. se la stringa P+C è presente nel dizionario
        P:= P+C (estendiamo Pcon C);
   altrimenti:
1. restituisci in output:
• la stringa del dizionario corrispondente a P (se P è vuoto, ritorna a zero);
• C, nella stessa forma come input del  fulsso da comprimere;
2. inseriamo la stringa P+C al dizionario;
3. P:= vuoto;
4. se ci sono ancora caratteri da comprimere
         si ritorna al passo 2;
   altrimenti se P non è vuoto
   
   1. ritorna la codifica della parola corrispondente a P;
   2. END.

Per quanto riguarda la decodifica, nella fase iniziale il dizionario è vuoto e viene ricostruito nel processo di decodifica. In ogni passo la codifica della coppia (W, C) è letta dalla sequenza da decodificare. Le stringhe W e C sono l'output e la stringa (stringa W + C) è inserita nel dizionario. Dopo la decodifica il dizionario avrà gli stessi contenuti che dopo la codifica.

Il principale vantaggio rispetto all'algoritmo LZ77 è il ridotto numero di confronti tra stringhe in ogni passo di codifica. Per quanto riguarda il rapporto di compressione, questo è simile a quello di LZ77.

4.2.4 LZW

In questo algoritmo [7], a differenza di LZ78 nella fase di codifica vengono restituiti in output solo i codici delle parole. Questo significa che il dizionario non può essere vuoto all'inizio di questa fase,  infatti conterrà tutte le stringhe di un solo carattere (root) dei dati in input. Poichè tutte le root sono già nel dizionario, ogni passo di codifica inizia con un prefisso di un carattere, così che la prima stringa cercata nel dizionario avrà due caratteri: il carattere con il quale inizia il nuovo prefisso e l'ultimo carattere della precedente stringa (C). Questo è necessario per permettere all'algoritmo di decodifica di ricostruire il dizionario senza l'aiuto di caratteri espliciti nella sequenza codificata

 L' algoritmo di codifica
All'inizio, il dizionario contiene tutte le possibili root, e P è vuoto;

1. C:= prossimo carattere;
2. se P+C è presente nel dizionario
   
      P:= P+C (estendi P con C);
altrimenti:
1. dai in output il codice che denota P nella codifica;
2. inserisci la stringa P+C nel dizionario;
3. P:= C (P ontiene solo il carattere C)
3. se ci sono altri caratteri da codificare
         vai al passo 2;
   altrimenti:
   1. dai in output il codice che denota P nella codifica;
   2. END.

Questo metodo ha avuto grande utilizzo poichè più veloce rispetto agli algoritmi basati LZ77, infatti ci sono molti  meno confronti tra stringhe.