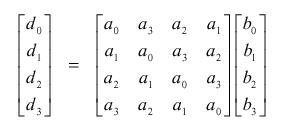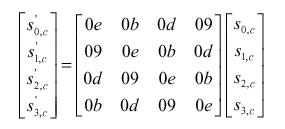Rijndael è un cifrario
a blocchi con una lunghezza del blocco e della chiave variabile. La
lunghezza del blocco è di 128 bit, mentre la lunghezza della
chiave, utilizzata nella cifratura, può essere di 128, 192
o 256 bit. Inoltre Rijndael è stato progettato per essere utiilizzato
con aggiuntive lunghezze del blocco e della chiave, tuttavia queste non
vengono prese in considerazione nello standard. Lo standard prevede una
lunghezza del blocco di 128 bit, 16 byte, ed una lunghezza della chiave
di 128 bit, definendo così Rijndael come nuovo standard AES-128
(128 indica la lunghezza della chiave). Comunque sono prese in considerazione
anche le altre due lunghezze della chiave 192 e 256, ottenendo così
le versioni AES-192 e AES-256. Tali problematiche verranno trattate e chiarite
in seguito, quando verranno presentate le specifiche dell'algoritmo. La
presentazione dell'algoritmo parte da alcune notazioni e convenzioni che
sono utilizzate nella descrizione dell'algoritmo. Sono riportati, quindi,
alcuni fondamentali preliminari matematici, infatti nelle varie fasi dell'algoritmo
vengono utilizzati procedimenti matematici che realizzano il disegno schematico.
Si prosegue con la specifica delle operazioni di espansione della chiave,
di cifratura e decifratura, per poi concludere con una implementazione
in C ed alcune considerazioni sulle prestazioni.
1. Schema
razionale e convenzioni
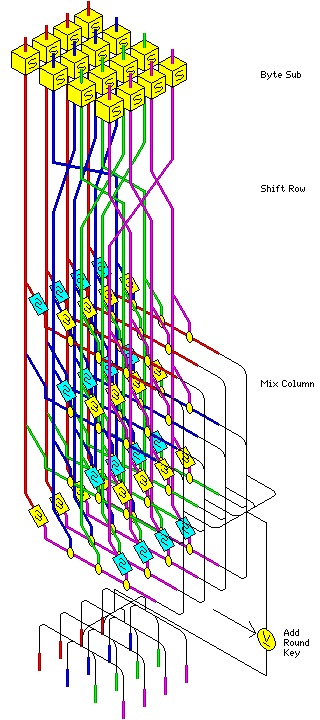
Il cifrario Rijndael utilizza semplici
operazioni orientate ai byte impiegando una chiave di cifratura. Le varie operazioni
sono applicate ai byte del blocco di input in diversi round, il numero dei round
è variabile e dipende dalla lunghezza della chiave e del blocco. Ogni
round coinvolge quattro operazioni fondamentali con le quali si effettuano sostituzioni,
mescolanze e spostamenti dei byte di input creando in questo modo una non linearità
dei dati e di conseguenza una maggiore sicurezza. Tutte le operazioni sui dati
vengono effettuate su di un array bidimensionale, chiamato State, composto da
un certo numero di righe e colonne che memorizza i byte di input. Lo schema
razionale rappresentato in figura descrive ciò che avviene durante l'algoritmo
di cifratura.
| Infatti,
sono rappresentate le quattro operazioni fondamentali che caratterizzano
ogni round:
- SubBytes(),
questa operazione computa una sostituzione di byte utilizzando una tavola
di sostituzione nota come S-Box;
- ShiftRows(),
questa operazione realizza uno spostamento ciclico delle righe dello State
che contengono i byte dei dati di input;
- MixColumns(),
questa operazione realizza una mescolanza dei byte nelle colonne dello
State;
- AddRoundKey(),
questa operazione realizza l'aggiunta di una Chiave di Round ai
byte dei dati.
L'operazione di sostituzione
dei byte impone, attraverso l'applicazione della S-Box, una certa non linearità
nei dati, mentre le operazioni successive di ShiftRows e MixColumns
realizzano
una mescolanza dei dati che ricorda un pò il famoso
CUBO DI RUBIK
nel
quale si possono mescolare i colori dei cubetti con spostamenti sulle righe
e sulle colonne. Per come è stato creato, questo cifrario realizza
la fase di decifratura di un blocco cifrato semplicemente invertendo alcune
delle operazioni citate. Queste operazioni inverse sono quindi applicate
in un numero di round analogo a quello computato nella cifratura.
Per entrare in argomentazioni
che prevedono un maggiore approfondimento degli algoritmi di cifratura
e decifratura, è indispensabile spiegare con alcune esemplificazioni
le notazioni e le convenzioni che il cifrario utilizza. D'altro canto sarà
ancora più importante trattare alcuni preliminari matematici in
quanto tutte le operazioni realizzate sui byte dei dati in realtà
sono applicazioni e trasformazioni matematiche che sottointendono concetti
algebrici a volte complessi.
|
 |
1.1
Input ed Output
L'input e l'output dell'algoritmo
consistono in una sequenza di 128 bit. Spesso ci si riferisce a questa
sequenza con il termine di "blocco" e al numero di bit che la compongono
con il termine di lunghezza del blocco. La chiave di cifratura è
una sequenza di 128, 192 o 256 bit. I bit di tali sequenze saranno numerati
partendo da 0, pertanto il valore i legato ad ogni bit è
un indice che varia nel range 0 < i<
128, 0 < i
<192 oppure
0 < i < 256, a secondo della
lunghezza del blocco e della chiave.
1.2 Byte
L' unità di base nella
computazione di Rijndael è il byte, una sequenza di 8 bit
trattata come una singola entità. L'input, l'output e la chiave
di cifratura sono processati come degli array di byte, ottenuti suddividendo
le sequenze in gruppi di 8 bit contigui. Alle sequeze di byte ci si riferisce
utilizzando l'array in cui esse sono memorizzate, ad esempio a[n], dove
il valore n può variare nel range:
lunghezza della chiave
= 128 bit,
con 0 < n < 16
lunghezza della chiave
= 192 bit,
con 0 < n < 24
lunghezza della chiave
= 256 bit,
con 0 < n < 32
lunghezza del blocco
= 128 bit,
con 0 < n < 16
E' utile anche rappresentare
i valori dei byte utilizzando la notazione esadecimale, nella quale i gruppi
di 8 bit vengono divisi in due gruppi da quattro ed ognuno dei due
rappresenta un carattere tra 0, ..., 9, a, ..., f (come mostrato in figura).
|
Bit Pattern
|
Character
|
|
0 0 0 0
|
0
|
|
0 0 0 1
|
1
|
|
0 0 1 0
|
2
|
|
0 0 1 1
|
3
|
|
|
Bit Pattern
|
Character
|
|
0 1 0 0
|
4
|
|
0 1 0 1
|
5
|
|
0 1 1 0
|
6
|
|
0 1 1 1
|
7
|
|
|
Bit Pattern
|
Character
|
|
1 0 0 0
|
8
|
|
1 0 0 1
|
9
|
|
1 0 1 0
|
a
|
|
1 0 1 1
|
b
|
|
|
Bit Pattern
|
Character
|
|
1 1 0 0
|
c
|
|
1 1 0 1
|
d
|
|
1 1 1 0
|
e
|
|
1 1 1 1
|
f
|
|
Ad esempio l'elemento { 0
1 1 0 0 0 1 1 } può essere rappresentato come { 6 3 }, dove i quattro
bit più significativi formano il valore 6, mentre i restanti bit
formano il valore 3.
1.3 Array di byte
Gli array di byte sono rappresentati
nella seguente forma:
a0 a1 a2 . . .a15
L'ordine dei bit rispetto
ai byte viene definito dalla sequenza di 128 bit di input
input0 input1
input2 . . . input126 input127 (
sequenza di input 128 bit)
come segue:
a0 = { input0,
input1, . . ., input7};
a1 = { input8,input9,
. . ., input15};
(ordine dei bit tra i byte)
.
.
.
a15 = { input120,
input121, . . ., input127};
La figura mostra come i bit sono
numerati in ogni byte, considerando insieme le definizioni dei par. 1.3 e 1.2:

1.4 Lo State
Internamente, le operazioni
dell'algoritmo sono eseguite su di un array bidimensionale di byte chiamato
State. Lo State consiste di quattro righe di byte, ognuna contenente Nb
byte, dove Nb è la lunghezza del blocco divisa per
32. Nell'array State, denotato con il simbolo s, ogni byte ha due indici,
l'indice di riga r varia nel range 0 <
r < 4, l'indice di colonna c varia nel range 0 <
c < Nb (per lo standard
Nb = 4, pertanto
c varia nel range 0< c <4).
All'inizio della cifratura
o della decifratura, come vedremo, l'input, memorizzato nell'array in[],
viene copiato nell'array State. Tutte le operazioni vengono effettuate
su questo array, quindi il suo valore finale viene copiato nell'array di
byte di output, out[].
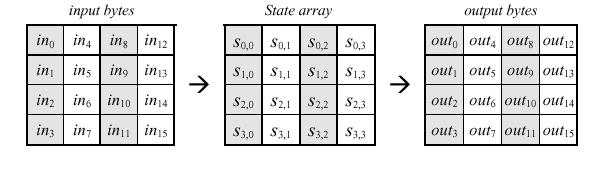
All'inizio della cifratura o della
decifratura, l'array di input in[] è copiato nell'array State in accordo
con lo schema:
s[r, c] = in[r + 4c]
con r compreso tra con 0 <
r < 4 e c compreso tra 0<
c < Nb
alla fine della cifratura o della
decifratura, l'array State viene copiato nell'array di output out[] come segue:
out[r
+ 4c] = s[r, c]
con r compreso tra con 0 <
r < 4 e c compreso tra 0<
c < Nb.
Si può notare che
i 4 byte nelle colonne dell'array State formano parole di 32 bit, dove
il numero di riga r stabilisce un indice per i 4 byte tra ogni parola.
1.5 Lo State come
Array di Colonne
Abbiamo detto che i 4 byte in ogni
colonna dell'array State formano parole di 32 bit, dove il numero di riga r stabilisce
un indice per i 4 byte tra ogni parola. Lo State può anche essere interpretato
come un array unidimensionale di parole di 32 bit, dove il numero di colonna c
stabilisce un indice in questo array. Ad esempio lo State può essere considerato
come un array di 4 parole, come segue:
w0 =a0
a1 a2 a3 w1
=a4
a5 a6 a7 w2
=a8
a9 a10 a11 w3
=a12
a13 a14 a15
dove abbiamo considerato che il
blocco di input consiste dei seguenti byte a0
a1 a2 . . .a15 e
che quindi viene mappato nell'array State:

2.
Preliminari matematici
Tutti i byte nell'algoritmo
sono interpretati come elementi di un "campo finito". Gli elementi di un
campo finito possono essere rappresentati in modi diversi, in questo caso
si è scelta la rappresentazione polinomiale.
Un byte b, formato dai bit
b7 b6 b5 b4 b3 b2 b1 b0, è considerato come un polinomio con coefficienti
in {0,1}:
b7 x7
+ b6 x6 + b5 x5+
b4 x4+ b3 x3+ b2
x2+ b1 x + b0
Esempio: il byte con valore
binario 01010111 corrisponde al polinomio:
x6+ x4+ x2+ x + 1.
Gli elementi di un campo
finito possono essere addizionati e moltiplicati, ma tali operazioni sono
diverse da quelle usate per i numeri.
2.1 Addizione
Nella rappresentazione polinomiale,
la somma di due elementi è il polinomio con coefficienti dati
dalla somma modulo 2 dei coefficienti, con potenze corrispondenti,
dei due termini.
Esempio:
(x6+ x4 + x2+ x + 1) + (x7+
x + 1) = x7+ x6+ x4+ x2.
In notazione binaria: "01010111"
+ "10000011" = "11010100".
Chiaramente, la somma modulo
2 coincide col lo XOR (denotato da  ) bit a bit dei due elementi, infatti si ha che 1
) bit a bit dei due elementi, infatti si ha che 1  1 = 0, 1
1 = 0, 1  0 = 1, e 0
0 = 1, e 0 0 = 0.
0 = 0.
In notazione esadecimale si ha:
{5 7 }  { 8 3 } = { d 4 }.
{ 8 3 } = { d 4 }.
La sottrazione mod 2 è
identica alla somma, dal momento che l' inverso di ogni elemento è
il proprio aggiuntivo.
2.2 Moltiplicazione
Nella rappresentazione polinomiale,
la moltiplicazione in GF(28) (con GF(28) denotiamo
il campo finito composto da 256 elementi), corrisponde alla
moltiplicazione dei polinomi modulo un polinomio binario irriducibile di
grado 8.
Un polinomio è irriducibile
se non ha altri divisori che 1 e se stesso. Il polinomio irriducibile
per Rijndael è indicato con m(x), ed è
dato da:
m (x) = x8+ x4
+ x3 + x + 1.
Esempio:
(x 6+ x4+ x2+ x + 1) (x7+ x
+ 1) = x13+ x11+ x9+
x8+ x7+x7+ x5+ x3+
x2+ x +x6+ x4+ x2+ x + 1
= x 13+ x11+ x9+ x8+
x6+ x5+ x 4+ x3+ 1 modulo
x8+ x4+ x3+ x + 1
= x 7+ x6+ 1
Chiaramente, il risultato
sarà
un polinomio binario di grado minore di 8, dal momento che si effettua
l'operazione di modulo con il polinomio irriducibile.
La moltiplicazione
è associativa ed è dotata di un elemento neutro { 01 }. Inoltre,
per qualunque polinomio binario b(x) di grado inferiore a 8, può
essere usato l'algoritmo esteso di Euclide per calcolare l'inverso moltiplicativo
di b(x), denotato con b -1 (x). L'algoritmo di Euclide
esteso calcola infatti i due polinomi a (x) e c (x) tali che:
b (x) a (x) + m (x) c (x)
= 1.
Questo implica che
a (x) · b (x) mod m (x) = 1 o b -1(x)
= a (x) mod m (x)
Inoltre, possiamo vedere
che a (x) · (b (x) + c (x)) = a (x) · b (x) + a (x) ·
c (x).
Ne consegue che l'insieme dei 256
possibili valori ottenuti con un byte, uniti allo XOR, utilizzato come addizione,
e alla moltiplicazione, formano la struttura del campo finito GF(28).
2.3 Polinomi con coefficicienti
in GF(28)
I polinomi con quattro termini possono
essere rappresentati con coefficienti che sono elementi di un campo
finito. Vediamo ad esempio:
a(x) = a3·x3 + a2·x2+
a1·x + a0·
che viene denotato in termini
di word nella forma [a0, a1, a2, a3].
Bisogna notare che i polinomi
definiti in questo modo si comportano in maniera piuttosto differente dai
polinomi usati per definire gli elementi di un campo finito, anche se utilizzano
entrambi lo stesso valore indeterminato x. Infatti, i coefficienti
dei polinomi che stiamo adesso considerando sono essi stessi degli elementi
di un campo finito, sono in questo caso byte, mentre nella definizione
precedente erano bit. Così, un vettore di 4 byte corrisponde ad
un polinomio di grado minore di 4 con coefficienti nel campo finito GF(28).
Questi polinomi possono essere addizionati sommando semplicemente i coefficienti
aventi potenze di x corrispondenti. La somma equivale ad una operazione
di XOR tra byte corrispondenti in ognuna delle word.
a(x) + b(x) = (a3  b3 )·x3 + (a2
b3 )·x3 + (a2  b2 )·x2 + (a1
b2 )·x2 + (a1 b1 )·x + (a0
b1 )·x + (a0  b0 )
b0 )
La moltiplicazione è
più complicata. Supponiamo di avere due polinomi con coefficienti
nel campo finito GF(28):
a(x) = a3 x3+a2
x2+a1 x + a0 e
b(x) = b3 x3+
b2 x2+ b1 x + b0.
Il loro prodotto c (x) =
a (x) b (x) è dato da:
c (x) = c6 x6+c5
x5 + c4x4+ c3 x3+
c2 x2+c1 x + c0
con
c0 = a0·
b0
c4 = a3· b1  a2· b2
a2· b2 a1· b3
a1· b3
c1 = a1·
b0  a0· b1
c5 = a3· b2
a0· b1
c5 = a3· b2  a2· b3
a2· b3
c2 = a2·
b0  a1· b1
a1· b1 a0· b2
c6 = a3· b3
a0· b2
c6 = a3· b3
c3 = a3·
b0  a2· b1
a2· b1 a1· b2
a1· b2  a0· b3
a0· b3
Chiaramente, c (x) può essere
rappresentato da un vettore di 4 byte. Riducendo c (x) modulo un polinomio di
grado 4, il risultato può essere ridotto ad un polinomio di grado inferiore
a 4, in Rijndael viene utillizzato il polinomio
m(x ) = x4+ 1.
Dal momento che xi
mod ( x4+ 1) = x(i mod 4), il prodotto modulare di a(x)
e b (x), denotato con d (x) = a (x)  b (x), è dato da:
b (x), è dato da:
d (x) = d3 x3+
d2x2+ d1 x + d0
con
d0= a0·
b0  a3· b1
a3· b1 a2· b2
a2· b2  a1· b3
a1· b3
d1= a1·
b0  a0· b1
a0· b1 a3·
b2
a3·
b2  a2·
b3
a2·
b3
d2= a2·
b0  a1· b1
a1· b1 a0· b2
a0· b2  a3· b3
a3· b3
d3= a3·
b0  a2·
b1
a2·
b1 a1· b2
a1· b2  a0· b3
a0· b3
L'operazione che consiste
nella moltiplicazione di un polinomio fisso a (x), può essere scritta
come moltiplicazione matriciale, dove la matrice è una matrice circolare:
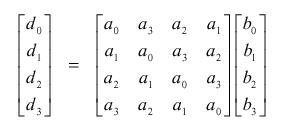
Dal momento che x4+
1 non è un polinomio irriducibile sul campo finito
GF(28), la moltiplicazione con un fissato polinomio di 4 termini
non è necessariamente invertibile. Pertanto Rijndael specifica un fissato
polinomio con 4 termini che ha un inverso moltiplicativo:
a(x) = {03}·x3
+
{01}·x2+ {01}·x + {02}
a-1(x)
= {0b}·x3 + {0d}·x2+ {09}·x + {0e}
che sarà utilizzato
nella cifratura e nella decifratura.
3.
Specifiche dell'algoritmo
La lunghezza fissata in Rijndael
del blocco di input, del blocco di output e dell'array State è di
128 bit. Tale lunghezza è rappresentata dal valore Nb
=4, che indica il numero di parole di 32 bit (numero di colonne ) nell'array
State.
La lunghezza della chiave di cifratura,
K, è di 128, 192, o 256 bit. Questa lunghezza è rappresentata
dal valore Nk = 4, 6, o 8, che indica il numero di parole di 32
bit nella chiave di cifratura. Le uniche possibili combinazioni di Round-Blocco-Chiave
conformi allo standard sono riportate nella seguente tabella:
| |
Key Length
(Nk words)
|
Block Size
(Nb words)
|
Number of Round
(Nr)
|
|
AES-128
|
4
|
4
|
10
|
|
AES-192
|
6
|
4
|
12
|
|
AES-256
|
8
|
4
|
14
|
Sia per la cifratura che
per la decifratura, Rijndael utilizza una funzione di round che si compone
di 4 differenti trasformazioni orientate ai byte:
1) la prima è una
trasformazione di sostituzione di byte, SubBytes(), che usa una tavola
di sostituzione (S-box);
2) la seconda è una
trasformazione di shift di righe con dei differenti offsets, ShiftRows();
3) la terza è una
trasformazione di mescolanza di dati tra ogni colonna dell'array State,
MixColumns();
4) la quarta è una trasformazione
che prevede l'aggiunta della Chiave di Round all' array State, AddRoundKey().
4. La Cifratura
All' inizio della cifratura, l'input,
memorizzato nell'array in[], viene copiato nell'array State usando le convenzioni
descritte precedentemente (par. 1.4). Dopo l' iniziale aggiunta di una Chiave
di Round(Round Key), l'array State viene trasformato con un ciclo di trasformazione
(Round Trasformation) di10, 12 o 14 round. Il numero dei round dipende dalla
lunghezza della chiave ed inoltre l'ultimo round differisce dai primi Nr-1.
Terminato il ciclo di trasformazione, lo State finale viene copiato nell'array
di output, out[]. La cifratura utilizza anche la chiave schedulata che consiste
in un array unidimensionale di word di 4 byte, denotato con w[], derivato dalla
funzione di espansione della chiave.
Ora viene descritta la cifratura
in pseudo-codice; le trasformazioni utilizzate SubBytes (), ShiftRows
(), MixColumns () e AddRoundKey () servono a processare
l'array State in moda da creare una non linearità nei dati di input.

Si può notare che
gli Nr round sono identici ad eccezione del round finale,
il quale non include la trasformazione MixColumns ().
L' algoritmo presentato
in pseudo-codice può essere schematizzato in un disegno che ben
chiarisce l'ordine delle trasformazioni applicate al blocco di input durante
la cifratura.
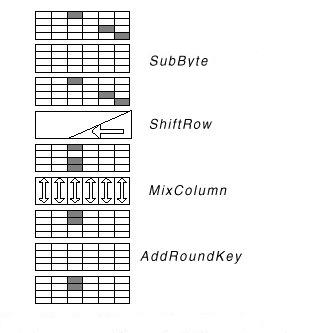
4.1 SubBytes ()
La trasformazione SubBytes
() è una sostituzione non-lineare che opera indipendentemente
su ogni byte dello State usando una tavola di sostituzione (o S-box). Questa
S-Box è invertibile ed è costruita dalla composizione
di due trasformazioni:
1. prima, prendendo l'inverso
moltiplicativo in GF(28) (l'elemento { 0 0 } rimane {
0 0 });
2. poi, applicando una trasformazione
affine su GF(28) definita da:
b'i
= bi  b(i+4) mod 8
b(i+4) mod 8 b(i+5) mod 8
b(i+5) mod 8 b(i+6) mod 8
b(i+6) mod 8 b(i+7) mod 8
b(i+7) mod 8  ci
ci
per i che varia
tra 0 < i < 8, dove bi
è
l' i-esimo bit del byte, e ci è l' i-esimo bit di un
byte c con il valore { 6 3 } in esadecimale oppure{ 0 1 1 0 0 0 0 1 1 }
in binario. L'apice sulla variabile b' indica che la variabile sta per
essere aggiornata con il valore di destra. In forma matriciale,
l' elemento della S-Box prodotto
dalla trasformazione affine può essere espresso come:

La figura seguente illustra
l' effetto della trasformazione SubBytes () sull'array State.
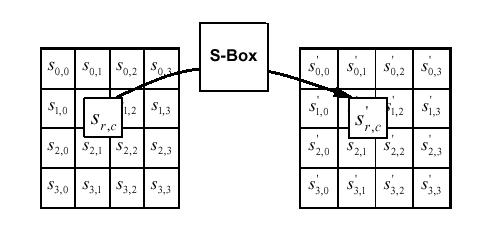
La S-Box usata nella trasformazione
SubBytes
() viene ora presentata in forma esadecimale:
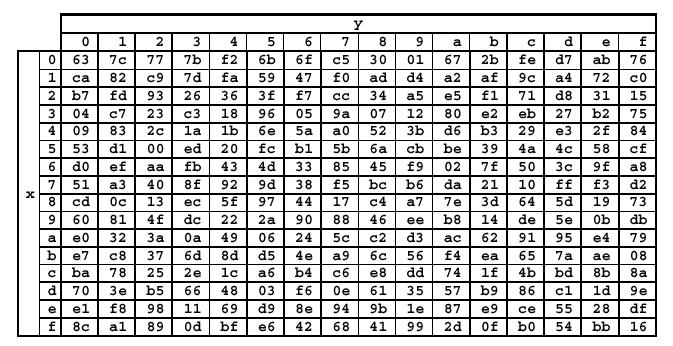
Ad esempio, se s1,1
= { 5 3 }, allora il valore della sostituzione dovrebbe essere determinato
dall'intersezione della riga di indice ' 5 ' con la colonna di indice '
3 '. Il risultato di tale sostituzione sarebbe dunque il valore s'1,1
=
{ e d }.
Il criterio della struttura
per la S-box è inspirato alla crittoanalisi differenziale e lineare
ed ad attacchi che usano manipolazioni algebriche, come attacchi di interpolazione,
oltre ad:
1. Invertibilità;
2. Minimizzazione della più
grande correlazione non-banale tra combinazioni lineari di bit d'input
e combinazione lineare di bit dell'output;
3. Minimizzazione del più
grande valore non-banale nella tavola di XOR;
4. La complessità
della sua espressione algebrica in GF(28);
5. La semplicità di descrizione.
4.2 ShiftRows ()
Nella trasformazione ShiftRows
(), i byte nelle ultime tre righe dell'array State sono spostati
(shiftati) ciclicamente
di un numero diverso di posizioni (offsets). La prima riga non viene shiftata.
La trasformazione procede nel modo
seguente:
s'r,c
= sr,(c+shift(r,Nb)) mod Nb
per 0 < r < 4
e 0 < c <
Nb
dove il valore dello spostamento
shift(r,Nb) dipende dal numero di riga, r, nel seguente modo
( ricordiamo che Nb nello standard è uguale a 4):
shift(1,4)
= 1 ; shift(2,4) = 2 ; shift(3,4) = 3.
La trasformazione può essere
illustrata con la seguente figura:
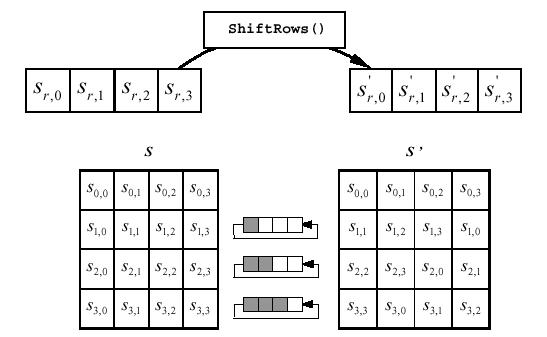
4.3 MixColumns ()
La
trasformazione MixColumns () opera sulle colonne dell'array
State.Le colonne sono trattate come polinomi di 4 termini con coefficienti
nel campo finito GF(28) e sono moltiplicate modulo x4+
1 con un fissato polinomio a(x), dato da
a(x)
= {03}·x3
+ {01}·x2+ {01}·x
+ {02}.
Ciò
può essere scritto come una moltiplicazione matriciale. Il prodotto
modulare
s'(x) = a(x) 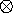 s(x) è dato da:
s(x) è dato da:

per 0 <
c < Nb
Come
risultato di questa moltiplicazione, i 4 byte in una colonna sono sostituiti
dai byte seguenti:
s'0,c
= ({02} · s0,c)  ({03} · s1,c)
({03} · s1,c)  s2,c
s2,c  s3,c
s3,c
s'1,c = s0,c  ({02} · s1,c)
({02} · s1,c)  ({03} · s2,c)
({03} · s2,c)  s3,c
s3,c
s'2,c = s0,c  s1,c
s1,c  ({02} · s2,c)
({02} · s2,c) ({03} · s3,c )
({03} · s3,c )
s'3,c = ({0b}
· s0,c )  s1,c
s1,c  s2,c
s2,c  ({0e} · s3,c )
({0e} · s3,c )
La trasformazione
può essere illustrata con la seguente figura:
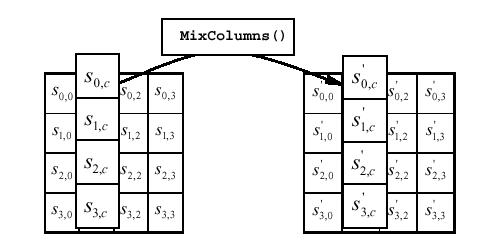
La trasformazione MixColumns
() è stata scelta secondo i seguenti criteri:
1. Invertibilità;
2. linearità in GF(28);
3. la velocità su
microprocessori a 8-bit;
4. la simmetria;
5. la semplicità di
descrizione.
I criteri 2, 4 e 5 hanno condotto
alla scelta del modulo della moltiplicazione polinomiale x4+1, i
criteri 1, 3 impongono le condizioni sui coefficienti. Il criterio 3 impone
che i coefficienti abbiano valori piccoli, in ordine di preferenza {00}, {01},
{02}, {03}.
4.4 AddRoundKey ()
In
questa trasformazione, una Chiave di Round (Round Key) è aggiunta allo
State attravero una semplice operazione di XOR bit a bit. Ogni Round key
consiste di Nb word della chiave schedulata. Queste Nb
word sono aggiunte ognuna nelle colonne dell'array State nel seguente modo:
[ s'0,c , s'1,c
, s'2,c , s'3,c ] = [ s0,c , s1,c
, s2,c , s3,c ] [ wround*Nb+c ]
per 0 < c < Nb
[ wround*Nb+c ]
per 0 < c < Nb
dove
le [ wi ] sono le word della chiave schedulata,
come sarà descritto in seguito, e dove round è un valore nel range
0 < round < Nr. Nella
cifratura, la prima addizione della Round Key avviene quando round = 0, prima
dell'applicazione della funzione di round. L'applicazione della trasformazione
AddRoundKey () negli Nr round della cifratura si
verifica invece quando 1 < round <Nr.
L'azione
della trasformazione è illustrata nella seguente figura, dove l
= round * Nb.
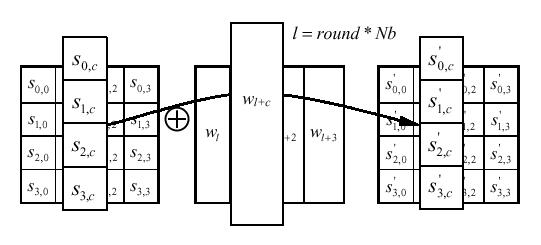
5. Espansione della chiave
Rijndael utilizza una chiave di cifratura
K e implementa una routine di espansione della chiave per generare una chiave
schedulata. L'algoritmo di espansione della chiave genera un totale di Nb*(
Nr +1) word: l'algoritmo di cifratura richiede un insieme iniziale
di Nb word, ed ognuno degli Nr round richiedono Nb
word della chiave. La chiave schedulata risultante consiste di un array lineare
di word di 4 byte, denotato con [ wi ], con i che varia tra
0 < i < Nb (Nr
+ 1). L'espansione della chiave di input nella chiave
schedulata può essere descritta in pseudo-codice, dove SubWord () è
una funzione che prende in input una word di 4 byte e applica la S-Box ad ognuno
dei 4 byte per produrre una word di output. La funzione RotWord () prende una
word [a0,a1,a2,a3] come input, esegue
una permutazione ciclica e restituisce una word [a0,a1,a2,a3].
Viene anche utilizzato un array di word costanti, Rcon [ i ], che contiene i valori
dati da [ xi-1, { 0 0 }, { 0 0 }, { 0 0 } ], con xi-1 che
rappresenta l' (i-1)-esima potenza di x nel campo GF(28) (x è
uguale a { 0 2 }). Bisogna notare inoltre che la variabile i inizia con
il valore di 1 anziché 0.

Si può notare dalla figura
che le prime Nk word della chiave espansa sono ottenute direttamente
dalla chiave di cifratura, mentre ogni word successiva, w[ i ], è uguale
allo XOR della word precedente, w[ i-1 ], con la word di Nk posizioni
più indietro. Per le word con posizioni che sono multiple di Nk,
viene applicata a w[ i-1 ] una trasformazione prima dello XOR, seguita da uno
XOR con una costante di round, Rcon[ i ]. Questa trasformazione consiste di
uno shift ciclico dei byte in una word (RotWord () ), seguito
da una funzione SubWord () che applica una S-Box a tutti e quattro
i byte della word. E' impotante notare che l'algoritmo di espansione della chiave
per una chiave di 256 bit ( Nk = 8) si compota diversamente rispetto
ad una chiave di 128 o 192 bit. Se Nk = 8 ed i-4 è multiplo
di Nk, la trasformazione SubWord () è applicata a w[ i-1
] prima dello XOR.
La funzione dell'algoritmo di espansione
della chiave è quella di provvedere alla resistenza contro i seguenti
tipi di attacco:
- Attacchi nei quali
parte della cifratura della chiave è conosciuta al crittoanalista;
- Attacchi nei quali la cifratura
della chiave è conosciuta e la cifratura è usata come
funzione di compressione di una funzione;
- Attacchi Related-Key.
Una condizione necessaria
per resistere agli attacchi Related-Key è quella di non avere
mai due cifrature della chiavi diverse che abbiano un insieme di
Round key in comune.
L'espansione della chiave
ha un ruolo importante anche nell'eliminazione di simmetrie:
- Simmetria nella Round
Trasformation: essa tratta tutti i byte di uno State nello stesso modo.
Questa simmetria può essere rimossa avendo round
costanti nella schedulazione
della chiave;
- Simmetria tra i round:
la Round Trasformation è la stessa per tutti i round.
Questa uguaglianza può
essere rimossa avendo round dipendenti e costanti nella schedulazione della
chiave.
L'espansione della chiave
è stata scelta secondo i seguenti criteri:
- Utilizzo di trasformazioni
invertibili,infatti conoscere ogni Nk parole
consecutive della chiave espansa permetterà di rigenerare
la tavola completa;
- Velocità su una
serie larga di microprocessori;
- l'uso di costanti
round per eliminare simmetrie;
- la diffusione di
cifrature della chiave differenti nelle Round Key;
- la conoscenza di
una parte della cifratura della chiave o pezzi di Round Key non permetterà
di calcolare
molte altre parti di Round
Key.
- Sufficienti non-linearità
per proibire la piena determinazione di Round Key differenti da cifrature
di chiavi differenti;
- La semplicità di
descrizione.
6. La decifratura
Le trasformazioni utilizzate
nella cifratura possone essere invertite e poi implementate in ordine inverso
producendo in questo modo l'algoritmo di decifratura.
Nella realizzazione della
decifratura è essenziale che l'unico passo non-lineare (SubBytes
()
) sia la prima trasformazione in un round e che le righe siano spostate
prima che MixColumns () sia applicata. Nel inverso di un
round, l'ordine delle trasformazioni è invertito, di conseguenza
il passo non-lineare finirà per essere l'ultimo passo del round
inverso e le righe saranno spostate dopo l'applicazione dell'inverso di
MixColumns
().
La struttura di Rijndael
è tale che la sequenza di trasformazioni nella decifratura è
uguale a quella della cifratura, con le trasformazioni sostituite dal loro
inverso ed una modifica nella schedulazione della chiave.
Le trasformazioni utilizzate
nella decifratura, InvShiftRows (), InvSubBytes
(), InvMixColumns () e AddRoundKey (), processano
l'array State che contiene il testo cifrato e producono come risultato
il testo in chiaro.
La decifratura viene ora
descritta mediante pseudo-codice, dove l'array w[ ] contiene la chiave
schedulata, ottenuta con l'algoritmo di espansione della chiave descritto
precedentemente.

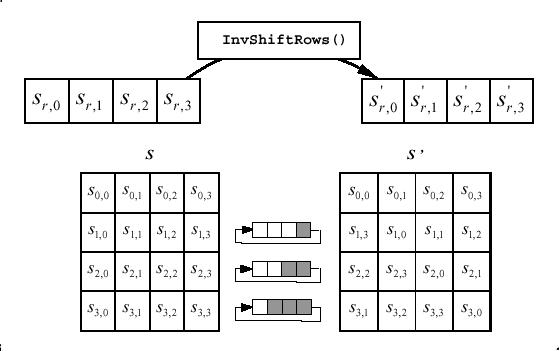
6.1 InvShiftRows ()
InvShiftRows() è
la trasformazione inversa di ShiftRows (). I byte nelle ultime tre
righe dell'array State sono shiftati ciclicamente di un diverso numero di byte
(offsets). La prima riga non viene shiftata. Le tre righe più in basso
sono shiftate ciclicamente di Nb - shift(r, Nb) byte,
dove il valore di shift(r, Nb) dipende dal numero di riga nel seguente
modo:
shift(1,4) = 1 ; shift(2,4) = 2 ; shift(3,4) = 3.
Precisamente, la trasformazione
InvShiftRows () procede come segue:
sr,(c+shift(r,Nb))
mod Nb = s'r,c
per 0 < r < 4
e 0 < c <
Nb
La trasformazione può anche
essere illustrata con una figura:
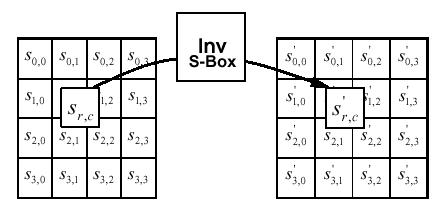
6.2 InvSubBytes ()
La trasformazione InvSubBytes
() realizza una sostituzione dei byte applicando l'inverso della S-box
ad ogni byte dell'array State. Questa S-Box inversa è costruita dalla
composizione di due trasformazioni:
1. prima, applicando l'inverso
della trasformazione affine descritta precedentemente(par. 4.1),
2. poi, prendendo l'inverso
moltiplicativo nel campo finito GF(28).
La trasformazione di sostituzione
procede in modo del tutto analogo a quello descritto nella fase di cifratura:
L' inverso della S-Box, usata nella
trasformazione, è presentata nella seguente figura in notazione esadecimale:
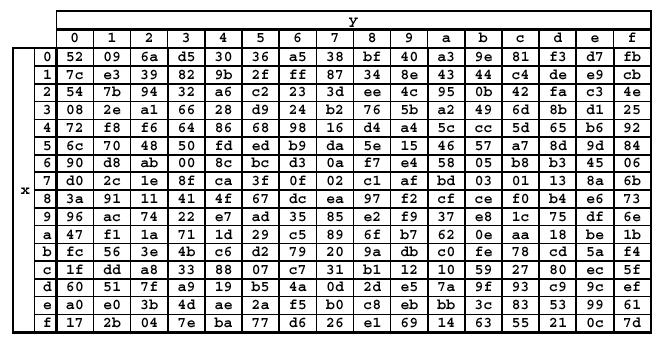
Ad esempio, se s1,1
= { e 3 }, allora il valore della sostituzione viene determinato dall'intersezione
della riga di indice ' 5 ' con la colonna di indice ' 3 '. Il risultato
di tale sostituzione è dunque il valore s'1,1
= { 4 d
}.
6.3 InvMixColumns ()
InvMixColumns
() è la trasformazione inversa di MixColumns(). La trasformazione
opera sull'array State da colonna a colonna, e considera ogni colonna come un
polinomio di 4 termini. Le colonne rappresentano polinomi con coefficienti nel
campo finito GF(28) che sono moltiplicati modulo
x4+ 1 con un fissato polinomio
a-1(x), dato da:
a-1(x) = {0b}·x3
+
{0d}·x2+ {09}·x + {0e}.
Ciò può essere scritto
come prodotto matriciale:
s'(x) = a-1(x)  s(x), ossia:
s(x), ossia:
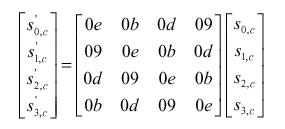
per 0 <
c < Nb
Come risultato di questa moltiplicazione,
i 4 byte di ogni colonna sono rimpiazzati dai seguenti byte:
s'0,c= ({0e} ·
s0,c)  ({0b}
· s1,c)
({0b}
· s1,c) ({0d} · s2,c)
({0d} · s2,c)  ({09}
· s3,c)
({09}
· s3,c)
s'1,c= ({09} ·
s0,c)  ({0e}
· s1,c)
({0e}
· s1,c) ({0b}
· s2,c)
({0b}
· s2,c)  ({0d}
· s3,c)
({0d}
· s3,c)
s'2,c= ({0d} ·
s0,c)  ({09}
· s1,c)
({09}
· s1,c) ({0e} · s2,c)
({0e} · s2,c) ({0b}
· s3,c)
({0b}
· s3,c)
s'3,c= ({0b} ·
s0,c)  ({0d}
· s1,c)
({0d}
· s1,c) ({09}
· s2,c)
({09}
· s2,c)  ({0e}
· s3,c)
({0e}
· s3,c)
Possiamo quindi illustrare la trasformazione
con la seguente figura:
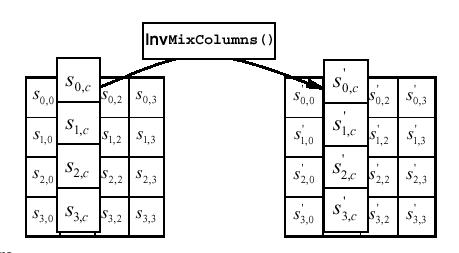
6.4 InvAddRoundKey ()
La trasformazione AddRoundKey
(), descritta precedentemente nel par. 4.4, ha come
sua trasformazione inversa sé stessa. Questo è dovuto al
fatto che la trasformazione utilizza soltanto un' operazione di XOR che,
come è noto, coincide con l'operazione inversa.
7. Implementazione
Segue un implementazione di Rijndael
in C++ di Brian
Gladman:
#ifndef __RIJNDAEL_ALG_H
#define __RIJNDAEL_ALG_H
#define MAXBC (256/32)
#define MAXKC (256/32)
#define MAXROUNDS 14
typedef unsigned char word8;
typedef unsigned short word16;
typedef unsigned long word32;
int rijndaelKeySched (word8
k[4][MAXKC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC]);
int rijndaelEncrypt (word8
a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC]);
int rijndaelEncryptRound
(word8 a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC],
int rounds);
int rijndaelDecrypt (word8
a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC]);
int rijndaelDecryptRound
(word8 a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC],
int rounds);
#endif
/* __RIJNDAEL_ALG_H
*/
/* rijndael-alg-ref.c
v2.0 August '99
* Reference ANSI
C code
* authors: Paulo
Barreto
* Vincent Rijmen
*/
/*
#include <stdio.h>
#include <stdlib.h>
#include "rijndael-alg-ref.h"
#define SC ((BC - 4) >> 1)
#include "boxes-ref.dat"
static word8 shifts[3][4][2]
= {
0, 0, 1, 3,
2, 2, 3, 1,
0, 0, 1, 5,
2, 4, 3, 3,
0, 0, 1, 7,
3, 5, 4, 4
};
word8 mul(word8 a, word8
b) {
/* vengono moltiplicati
due elementi di GF(28)
* necessari
per MixColumn e InvMixColumn
*/
if (a
&& b)
return Alogtable[(Logtable[a] + Logtable[b])%255];
else
return 0;
}
void KeyAddition(word8 a[4][MAXBC],
word8 rk[4][MAXBC], word8 BC) {
int i,
j;
for(i
= 0; i < 4; i++)
for(j = 0; j < BC; j++)
a[i][j] ^= rk[i][j];
}
void ShiftRow(word8 a[4][MAXBC],
word8 d, word8 BC) {
/* La riga 0
rimane inalterata
* Le altre tre righe
sono shiftate di una lunghezza variabile
*/
word8
tmp[MAXBC];
int i,
j;
for(i
= 1; i < 4; i++) {
for(j = 0; j < BC; j++)
tmp[j] = a[i][(j + shifts[SC][i][d]) % BC];
for(j = 0; j < BC; j++) a[i][j] = tmp[j];
}
}
void Substitution(word8 a[4][MAXBC],
word8 box[256], word8 BC) {
/* Sostituisce ogni
byte di input con byte ottenuti
* con una trasformazione
non lineare S-box
*/
int i,
j;
for(i
= 0; i < 4; i++)
for(j = 0; j < BC; j++)
a[i][j] = box[a[i][j]] ;
}
void MixColumn(word8 a[4][MAXBC],
word8 BC) {
/* Mescola quattro
byte di ogni colonna in maniera lineare*/
word8
b[4][MAXBC];
int i,
j;
for(j
= 0; j < BC; j++)
for(i = 0; i < 4; i++)
b[i][j] = mul(2,a[i][j]) ^ mul(3,a[(i + 1) % 4][j]) ^ a[(i + 2) % 4][j]
^ a[(i + 3) % 4][j];
for(i
= 0; i < 4; i++)
for(j = 0; j < BC; j++)
a[i][j] = b[i][j];
}
void InvMixColumn(word8 a[4][MAXBC],
word8 BC) {
/* Mescola i quattro
byte di ogni colonna in modo lineare
* Questa è
l'operazione inversa di Mixcolumn
*/
word8
b[4][MAXBC];
int i,
j;
for(j
= 0; j < BC; j++)
for(i = 0; i < 4; i++)
b[i][j] = mul(0xe,a[i][j]) ^ mul(0xb,a[(i + 1) % 4][j]) ^ mul(0xd,a[(i
+ 2) % 4][j]) ^ mul(0x9,a[(i + 3) % 4][j]);
for(i
= 0; i < 4; i++)
for(j = 0; j < BC; j++)
a[i][j] = b[i][j];
}
int rijndaelKeySched (word8
k[4][MAXKC], int keyBits, int blockBits, word8 W[MAXROUNDS+1][4][MAXBC])
{
/* Vengono calcolate
i round delle chiavi
* Il numero
di calcoli dipende dai bit della chiave
*/
int KC,
BC, ROUNDS;
int i,
j, t, rconpointer = 0;
word8
tk[4][MAXKC];
switch
(keyBits) {
case 128: KC = 4; break;
case 192: KC = 6; break;
case 256: KC = 8; break;
default : return (-1);
}
switch
(blockBits) {
case 128: BC = 4; break;
case 192: BC = 6; break;
case 256: BC = 8; break;
default : return (-2);
}
switch
(keyBits >= blockBits ? keyBits : blockBits) {
case 128: ROUNDS = 10; break;
case 192: ROUNDS = 12; break;
case 256: ROUNDS = 14; break;
default : return (-3); /* this cannot happen */
}
for(j
= 0; j < KC; j++)
for(i = 0; i < 4; i++)
tk[i][j] = k[i][j];
t = 0;
for(j
= 0; (j < KC) && (t < (ROUNDS+1)*BC); j++, t++)
for(i = 0; i < 4; i++) W[t / BC][i][t % BC] = tk[i][j];
while
(t < (ROUNDS+1)*BC) {
for(i = 0; i < 4; i++)
tk[i][0] ^= S[tk[(i+1)%4][KC-1]];
tk[0][0] ^= rcon[rconpointer++];
if (KC
!= 8)
for(j = 1; j < KC; j++)
for(i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j-1];
else
{
for(j = 1; j < KC/2; j++)
for(i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j-1];
for(i = 0; i < 4; i++)
tk[i][KC/2] ^= S[tk[i][KC/2 - 1]];
for(j = KC/2 + 1; j < KC; j++)
for(i = 0; i < 4; i++)
tk[i][j] ^= tk[i][j-1];
}
for(j
= 0; (j < KC) && (t < (ROUNDS+1)*BC); j++, t++)
for(i = 0; i < 4; i++)
W[t / BC][i][t % BC] = tk[i][j];
}
return
0;
}
int rijndaelEncrypt (word8
a[4][MAXBC], int keyBits, int blockBits, word8 rk[MAXROUNDS+1][4][MAXBC])
{
int r,
BC, ROUNDS;
switch
(blockBits) {
case 128: BC = 4; break;
case 192: BC = 6; break;
case 256: BC = 8; break;
default : return (-2);
}
switch
(keyBits >= blockBits ? keyBits : blockBits) {
case 128: ROUNDS = 10; break;
case 192: ROUNDS = 12; break;
case 256: ROUNDS = 14; break;
default : return (-3);
}
KeyAddition(a,rk[0],BC);
for(r
= 1; r < ROUNDS; r++) {
Substitution(a,S,BC);
ShiftRow(a,0,BC);
MixColumn(a,BC);
KeyAddition(a,rk[r],BC);
}
Substitution(a,S,BC);
ShiftRow(a,0,BC);
KeyAddition(a,rk[ROUNDS],BC);
return
0;
}
int rijndaelEncryptRound
(word8 a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC],
int rounds)
{
int r,
BC, ROUNDS;
switch
(blockBits) {
case 128: BC = 4; break;
case 192: BC = 6; break;
case 256: BC = 8; break;
default : return (-2);
}
switch
(keyBits >= blockBits ? keyBits : blockBits) {
case 128: ROUNDS = 10; break;
case 192: ROUNDS = 12; break;
case 256: ROUNDS = 14; break;
default : return (-3); /* this cannot happen */
}
if (rounds
> ROUNDS) rounds = ROUNDS;
KeyAddition(a,rk[0],BC);
for(r
= 1; (r <= rounds) && (r < ROUNDS); r++) {
Substitution(a,S,BC);
ShiftRow(a,0,BC);
MixColumn(a,BC);
KeyAddition(a,rk[r],BC);
}
if (rounds
== ROUNDS) {
Substitution(a,S,BC);
ShiftRow(a,0,BC);
KeyAddition(a,rk[ROUNDS],BC);
}
return
0;
}
int rijndaelDecrypt (word8
a[4][MAXBC], int keyBits, int blockBits, word8 rk[MAXROUNDS+1][4][MAXBC])
{
int r,
BC, ROUNDS;
switch
(blockBits) {
case 128: BC = 4; break;
case 192: BC = 6; break;
case 256: BC = 8; break;
default : return (-2);
}
switch
(keyBits >= blockBits ? keyBits : blockBits) {
case 128: ROUNDS = 10; break;
case 192: ROUNDS = 12; break;
case 256: ROUNDS = 14; break;
default : return (-3);
}
KeyAddition(a,rk[ROUNDS],BC);
Substitution(a,Si,BC);
ShiftRow(a,1,BC);
for(r
= ROUNDS-1; r > 0; r--) {
KeyAddition(a,rk[r],BC);
InvMixColumn(a,BC);
Substitution(a,Si,BC);
ShiftRow(a,1,BC);
}
KeyAddition(a,rk[0],BC);
return
0;
}
int rijndaelDecryptRound
(word8 a[4][MAXBC], int keyBits, int blockBits,
word8 rk[MAXROUNDS+1][4][MAXBC],
int rounds)
{
int r,
BC, ROUNDS;
switch
(blockBits) {
case 128: BC = 4; break;
case 192: BC = 6; break;
case 256: BC = 8; break;
default : return (-2);
}
switch
(keyBits >= blockBits ? keyBits : blockBits) {
case 128: ROUNDS = 10; break;
case 192: ROUNDS = 12; break;
case 256: ROUNDS = 14; break;
gladmandefault : return (-3);
}
if (rounds
> ROUNDS)
rounds = ROUNDS;
KeyAddition(a,rk[ROUNDS],BC);
Substitution(a,Si,BC);
ShiftRow(a,1,BC);
for(r
= ROUNDS-1; r > rounds; r--) {
KeyAddition(a,rk[r],BC);
InvMixColumn(a,BC);
Substitution(a,Si,BC);
ShiftRow(a,1,BC);
}
if (rounds
== 0) {
KeyAddition(a,rk[0],BC);
}
return
0;
}
8. Prestazioni
Viene ora presentata una tabella
che riporta le prestazioni dell'algoritmo su un sistema con processore
Intel Pentium III.
I dati riportati sono
espressi in cicli Mbits/secondo dove M è uguale a 106
non 220.
| main
tables |
0 |
1 |
1 |
1 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
| last
round tables |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
4 |
4 |
4 |
4 |
4 |
4 |
| decryption
key schedule tables |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
4 |
4 |
| loop
unrolled |
n |
n |
n |
n |
n |
y |
n |
y |
n |
y |
n |
y |
n |
y |
n |
y |
128
bit
block
|
code size
(bytes) |
9666 |
5586 |
5634 |
5442 |
4386 |
10258 |
4386 |
10210 |
4194 |
10018 |
4162 |
9970 |
3858 |
9666 |
3698 |
9506 |
| table size
(bytes) |
576 |
2624 |
4672 |
6720 |
8768 |
8768 |
10816 |
10816 |
12864 |
12864 |
16960 |
16960 |
19008 |
19008 |
25152 |
25152 |
128
bit
key |
key (encrypt) |
451 |
455 |
386 |
425 |
455 |
455 |
392 |
386 |
419 |
420 |
313 |
317 |
363 |
359 |
342 |
358 |
| key (decrypt) |
562 |
1727 |
1630 |
1023 |
1704 |
1712 |
1629 |
1621 |
1026 |
1022 |
1624 |
1626 |
940 |
948 |
710 |
708 |
| encrypt |
2337 |
729 |
682 |
683 |
424 |
405 |
392 |
375 |
394 |
377 |
385 |
367 |
392 |
362 |
382 |
367 |
| decrypt |
2104 |
704 |
662 |
662 |
435 |
404 |
405 |
371 |
399 |
373 |
400 |
369 |
398 |
369 |
395 |
358 |
| enc (bits/cycle) |
0.055 |
0.176 |
0.188 |
0.187 |
0.302 |
0.316 |
0.327 |
0.341 |
0.325 |
0.340 |
0.332 |
0.349 |
0.327 |
0.354 |
0.335 |
0.349 |
| dec (bits/cycle) |
0.061 |
0.182 |
0.193 |
0.193 |
0.294 |
0.317 |
0.316 |
0.345 |
0.321 |
0.343 |
0.320 |
0.347 |
0.322 |
0.347 |
0.324 |
0.358 |
192
bit
key |
key (encrypt) |
380 |
374 |
340 |
353 |
374 |
374 |
341 |
344 |
347 |
353 |
303 |
298 |
279 |
281 |
272 |
272 |
| key (decrypt) |
507 |
1901 |
1862 |
1072 |
1902 |
1887 |
1869 |
1859 |
1077 |
1076 |
1866 |
1868 |
969 |
975 |
699 |
698 |
| encrypt |
2840 |
874 |
815 |
825 |
491 |
488 |
464 |
442 |
467 |
442 |
467 |
437 |
465 |
437 |
462 |
434 |
| decrypt |
2556 |
843 |
796 |
797 |
509 |
486 |
470 |
432 |
468 |
429 |
463 |
432 |
462 |
430 |
471 |
432 |
| enc (bits/cycle) |
0.045 |
0.146 |
0.157 |
0.155 |
0.261 |
0.262 |
0.276 |
0.290 |
0.274 |
0.290 |
0.274 |
0.293 |
0.275 |
0.293 |
0.277 |
0.295 |
| dec (bits/cycle) |
0.050 |
0.152 |
0.161 |
0.161 |
0.251 |
0.263 |
0.272 |
0.296 |
0.274 |
0.298 |
0.276 |
0.296 |
0.277 |
0.298 |
0.272 |
0.296 |
256
bit
key |
key (encrypt) |
568 |
598 |
493 |
482 |
598 |
598 |
493 |
493 |
480 |
483 |
412 |
409 |
398 |
398 |
407 |
409 |
| key (decrypt) |
722 |
2409 |
2278 |
1332 |
2403 |
2410 |
2290 |
2252 |
1332 |
1332 |
2282 |
2286 |
1231 |
1228 |
907 |
912 |
| encrypt |
3349 |
1019 |
964 |
969 |
579 |
555 |
549 |
521 |
553 |
518 |
548 |
510 |
553 |
510 |
545 |
505 |
| decrypt |
3022 |
978 |
944 |
912 |
590 |
569 |
563 |
503 |
565 |
503 |
554 |
506 |
555 |
499 |
551 |
500 |
| enc (bits/cycle) |
0.038 |
0.126 |
0.133 |
0.132 |
0.221 |
0.231 |
0.233 |
0.246 |
0.231 |
0.247 |
0.234 |
0.251 |
0.231 |
0.251 |
0.235 |
0.253 |
| dec (bits/cycle) |
0.042 |
0.131 |
0.136 |
0.140 |
0.217 |
0.225 |
0.227 |
0.254 |
0.227 |
0.254 |
0.231 |
0.253 |
0.231 |
0.257 |
0.232 |
0.256 |
192
bit
block
|
code size
(bytes) |
14402 |
8050 |
8114 |
7810 |
6114 |
15458 |
6162 |
15426 |
5858 |
15122 |
5890 |
15138 |
5522 |
14770 |
5250 |
14498 |
| table size
(bytes) |
612 |
2660 |
4708 |
6756 |
8804 |
8804 |
10852 |
10852 |
12900 |
12900 |
16996 |
16996 |
19044 |
19044 |
25188 |
25188 |
128
bit
key |
key (encrypt) |
813 |
880 |
685 |
734 |
882 |
880 |
689 |
693 |
723 |
724 |
575 |
575 |
635 |
634 |
663 |
649 |
| key (decrypt) |
1012 |
3171 |
2936 |
1812 |
3136 |
3133 |
2921 |
2923 |
1810 |
1805 |
2829 |
2828 |
1736 |
1722 |
1259 |
1267 |
| encrypt |
4486 |
1326 |
1249 |
1262 |
741 |
764 |
680 |
691 |
676 |
688 |
673 |
671 |
677 |
680 |
679 |
677 |
| decrypt |
3840 |
1242 |
1196 |
1192 |
726 |
733 |
662 |
657 |
665 |
657 |
647 |
649 |
651 |
648 |
652 |
649 |
| enc (bits/cycle) |
0.043 |
0.145 |
0.154 |
0.152 |
0.259 |
0.251 |
0.282 |
0.278 |
0.284 |
0.279 |
0.285 |
0.286 |
0.284 |
0.282 |
0.283 |
0.284 |
| dec (bits/cycle) |
0.050 |
0.155 |
0.161 |
0.161 |
0.264 |
0.262 |
0.290 |
0.292 |
0.289 |
0.292 |
0.297 |
0.296 |
0.295 |
0.296 |
0.294 |
0.296 |
192
bit
key |
key (encrypt) |
503 |
562 |
522 |
487 |
558 |
566 |
520 |
520 |
478 |
482 |
417 |
416 |
393 |
397 |
388 |
394 |
| key (decrypt) |
701 |
2810 |
2762 |
1561 |
2798 |
2824 |
2761 |
2750 |
1561 |
1565 |
2666 |
2683 |
1473 |
1478 |
1026 |
1021 |
| encrypt |
4485 |
1326 |
1257 |
1254 |
737 |
771 |
676 |
688 |
678 |
680 |
669 |
675 |
668 |
676 |
674 |
677 |
| decrypt |
3845 |
1255 |
1186 |
1186 |
724 |
730 |
664 |
655 |
658 |
653 |
652 |
645 |
656 |
649 |
655 |
655 |
| enc (bits/cycle) |
0.043 |
0.145 |
0.153 |
0.153 |
0.261 |
0.249 |
0.284 |
0.279 |
0.283 |
0.282 |
0.287 |
0.284 |
0.287 |
0.284 |
0.285 |
0.284 |
| dec (bits/cycle) |
0.050 |
0.153 |
0.162 |
0.162 |
0.265 |
0.263 |
0.289 |
0.293 |
0.292 |
0.294 |
0.294 |
0.298 |
0.293 |
0.296 |
0.293 |
0.293 |
256
bit
key |
key (encrypt) |
857 |
855 |
781 |
756 |
855 |
855 |
783 |
786 |
748 |
757 |
652 |
657 |
601 |
604 |
606 |
607 |
| key (decrypt) |
1087 |
3613 |
3438 |
2014 |
3517 |
3541 |
3437 |
3427 |
2018 |
2022 |
3311 |
3305 |
1893 |
1890 |
1348 |
1346 |
| encrypt |
5289 |
1559 |
1479 |
1488 |
864 |
860 |
803 |
795 |
803 |
792 |
795 |
782 |
795 |
791 |
790 |
786 |
| decrypt |
4529 |
1478 |
1394 |
1396 |
846 |
828 |
791 |
758 |
776 |
763 |
773 |
749 |
782 |
753 |
770 |
751 |
| enc (bits/cycle) |
0.036 |
0.123 |
0.130 |
0.129 |
0.222 |
0.223 |
0.239 |
0.242 |
0.239 |
0.242 |
0.242 |
0.246 |
0.242 |
0.243 |
0.243 |
0.244 |
| dec (bits/cycle) |
0.042 |
0.130 |
0.138 |
0.138 |
0.227 |
0.232 |
0.243 |
0.253 |
0.247 |
0.252 |
0.248 |
0.256 |
0.246 |
0.255 |
0.249 |
0.256 |
256
bit
blolck
|
code size
(bytes) |
19170 |
10578 |
10610 |
10210 |
7922 |
20594 |
7970 |
20514 |
7570 |
20114 |
7650 |
20194 |
7170 |
19714 |
6834 |
19378 |
| table size
(bytes) |
628 |
2676 |
4724 |
6772 |
8820 |
8820 |
10868 |
10868 |
12916 |
12916 |
17012 |
17012 |
19060 |
19060 |
25204 |
25204 |
128
bit
key |
key (encrypt) |
1318 |
1216 |
999 |
996 |
1218 |
1218 |
998 |
1000 |
979 |
979 |
857 |
843 |
981 |
966 |
911 |
984 |
| key (decrypt) |
1593 |
4703 |
4509 |
2681 |
4722 |
4732 |
4505 |
4489 |
2677 |
2682 |
4378 |
4336 |
2676 |
2683 |
1908 |
1939 |
| encrypt |
7106 |
2089 |
2015 |
2023 |
1175 |
1143 |
1098 |
1049 |
1102 |
1055 |
1095 |
1058 |
1086 |
1057 |
1093 |
1060 |
| decrypt |
6053 |
1976 |
1894 |
1895 |
1170 |
1135 |
1070 |
1043 |
1066 |
1042 |
1061 |
1036 |
1062 |
1042 |
1068 |
1032 |
| enc (bits/cycle) |
0.036 |
0.123 |
0.127 |
0.127 |
0.218 |
0.224 |
0.233 |
0.244 |
0.232 |
0.243 |
0.234 |
0.242 |
0.236 |
0.242 |
0.234 |
0.242 |
| dec (bits/cycle) |
0.042 |
0.130 |
0.135 |
0.135 |
0.219 |
0.226 |
0.239 |
0.245 |
0.240 |
0.246 |
0.241 |
0.247 |
0.241 |
0.246 |
0.240 |
0.248 |
192
bit
key |
key (encrypt) |
852 |
797 |
814 |
811 |
797 |
797 |
811 |
811 |
808 |
808 |
617 |
622 |
590 |
590 |
585 |
579 |
| key (decrypt) |
1124 |
4298 |
4289 |
2506 |
4312 |
4313 |
4311 |
4320 |
2501 |
2501 |
4147 |
4145 |
2293 |
2294 |
1546 |
1537 |
| encrypt |
7101 |
2098 |
2021 |
2039 |
1169 |
1149 |
1098 |
1051 |
1098 |
1059 |
1090 |
1057 |
1092 |
1055 |
1090 |
1055 |
| decrypt |
6053 |
1977 |
1883 |
1898 |
1164 |
1128 |
1068 |
1040 |
1068 |
1043 |
1057 |
1033 |
1061 |
1038 |
1062 |
1038 |
| enc (bits/cycle) |
0.036 |
0.122 |
0.127 |
0.126 |
0.219 |
0.223 |
0.233 |
0.244 |
0.233 |
0.242 |
0.235 |
0.242 |
0.234 |
0.243 |
0.235 |
0.243 |
| dec (bits/cycle) |
0.042 |
0.130 |
0.136 |
0.135 |
0.220 |
0.227 |
0.240 |
0.246 |
0.240 |
0.245 |
0.242 |
0.248 |
0.241 |
0.247 |
0.241 |
0.247 |
256
bit
key |
key (encrypt) |
1069 |
1106 |
974 |
963 |
1103 |
1104 |
976 |
974 |
961 |
961 |
804 |
802 |
759 |
769 |
756 |
756 |
| key (decrypt) |
1351 |
4615 |
4469 |
2653 |
4614 |
4620 |
4461 |
4451 |
2659 |
2655 |
4332 |
4321 |
2471 |
2478 |
1724 |
1728 |
| encrypt |
7102 |
2109 |
2016 |
2020 |
1175 |
1149 |
1097 |
1059 |
1098 |
1048 |
1091 |
1057 |
1098 |
1059 |
1096 |
1059 |
| decrypt |
6052 |
1983 |
1881 |
1891 |
1165 |
1136 |
1073 |
1040 |
1068 |
1042 |
1064 |
1032 |
1055 |
1035 |
1066 |
1036 |
| enc (bits/cycle) |
0.036 |
0.121 |
0.127 |
0.127 |
0.218 |
0.223 |
0.233 |
0.242 |
0.233 |
0.244 |
0.235 |
0.242 |
0.233 |
0.242 |
0.234 |
0.242 |
| dec (bits/cycle) |
0.042 |
0.129 |
0.136 |
0.135 |
0.220 |
0.225 |
0.239 |
0.246 |
0.240 |
0.246 |
0.241 |
0.248 |
0.243 |
0.247 |
0.240 |
0.247 |
I dati relativi alle performance
dell' algoritmo sono stati computati da Brian
Gladman: