4 Decimalization Attack

Presentiamo un attacco ai moduli di sicurezza dell'hardware utilizzato per la memorizzazione e la verifica dei PIN degli utenti di un servizio di bancomat.

Utilizzando PIN composti da quattro cifre se ne hanno 10000 differenti (da 0000 a 9999). Ad un malintenzionato che voglia indovinare il PIN corretto di un cliente del servizio di bancomat facendo dei tentativi a caso, occorrerebbero quindi in media 5000 tentativi.

Sfruttando un algoritmo che manipola le tavole di decimalizzazione adattive, in 30 minuti un attaccante può scoprire circa 7000 PIN invece dei circa 24 che riuscirebbe a scoprire con un attacco di forza bruta.

Supponendo che per ogni carta bancomat sia possibile prelevare in media 300 EURO al giorno, il bottino potenziale di un colpo messo a segno in un giorno cresce dai 7200 EURO ai 2100000 EURO.

Sicurezza bancaria

Le banche hanno intrapreso la strada della lotta contro le frodi: sia di quelle originate all'interno dello staff bancario, che di quelle originate da estranei.

Esse hanno sviluppato metodi di protezione contro le frodi dei membri interni introducendo contabilità a duplice inserimento, separazione delle funzionalità bancarie, periodi di vacanza obbligatori per lo staff, e riconoscendo la necessità di regolari verifiche della sicurezza. Questi metodi hanno successo nel ridurre le frodi ad un livello accettabile, e, in concomitanza ad una struttura legale  per stabilire le responsabilità in caso di frodi, possono anche proteggere il cliente della banca che usufruisce del servizio di bancomat.

Le pratiche bancarie tradizionali puntano sì a ridurre il numero delle frodi ad un livello accettabile, ma ciò si traduce scarsamente nell'individuazione di quali dovrebbero essere i requisiti di sicurezza; così spesso è impossibile stabilire se il manifestarsi di un difetto nel sistema possa considerarsi un caso isolato o la punta di un enorme iceberg. 

L'introduzione degli HSM (vedi paragrafo successivo) per proteggere i PIN dei clienti è stato un passo nella giusta direzione, ma fino al 2002 questi dispositivi non sono stati universalmente adottati e quelli che lo sono stati hanno dimostrato un sacco di volte di non essere immuni ad attacchi, come vedremo nel paragrafo 4.3 .

4.1 Scenario

     Figura 4.1.

Gli sportelli bancomat sono usati ogni giorno da milioni di intestatari di conti bancari per effettuare dei prelievi di denaro.

La loro vasta diffusione e i luoghi solitari in cui a volte essi sono ubicati li rende dei mezzi ideali per i criminali.

L'autenticazione dell'utente dello sportello bancomat è la misura di sicurezza primaria contro le frodi; la clonazione della carta bancomat è un'operazione banale in confronto all'acquisizione del PIN.

I programmatori di una banca hanno accesso al sistema informatico impiegato per la memorizzazione dei PIN degli intestatari dei conti, che normalmente consiste in un mainframe (vedi Figura 4.1) connesso con un solo HSM (Hardware Security Module, modulo di sicurezza hardware) che è tamper-resistant, cioè resistente ai tentativi più disparati di manomissione, ed ha un API (Application Programmer Interface, elenco di dati e funzioni che possono essere utilizzati dal programmatore) che risponde solo con un "sì" o con un "no" alle interrogazioni. 

Il sistema informatico della banca, su menzionato, può essere soggetto ad attacchi; un esempio di attacco  è quello di scrivere un programma per l'HSM che provi tutti i PIN, in forma cifrata o in chiaro, per un particolare conto bancario (vedi paragrafo 4.3). Un algoritmo di ricerca esaustiva, per un PIN di quattro cifre, dovrà provare in media 5000 possibili PIN prima di trovare quello giusto. Normalmente un HSM permette di testare circa 60 PIN al secondo, oltre al normale traffico di richieste. Facendo dei calcoli otteniamo che 5000 interrogazioni all'archivio dei PIN possono essere soddisfatte in un tempo che si aggira intorno agli 83,4 secondi. Dunque, sotto queste ipotesi, per scoprire 25 PIN corretti occorreranno 83,4×25 secondi, cioè 2085 secondi, ovvero circa 35 minuti.

Ad ogni modo, gli HSM, implementando diversi metodi di generazione del PIN, hanno dei difetti.

I primi ATM erano degli IBM 3624, introdotti negli Stati Uniti intorno al 1980, e molti dei metodi di generazione dei PIN sono basati ancora sul loro approccio.

Gli ATM basati sull'architettura degli IBM 3624 calcolano il PIN del cliente dal numero di conto bancario. Questo viene cifrato utilizzando il cifrario DES con una chiave segreta chiamata "chiave di generazione del PIN". La stringa ottenuta dalla cifratura DES è interpretata come una stringa esadecimale; sono necessarie le prime quattro cifre della stringa ottenuta, le altre sono scartate. Ognuna delle 4 cifre considerate è una delle seguenti: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Per convertire questo quartetto di cifre esadecimali in un PIN che possa essere digitato su una tastiera decimale, è necessaria una decimalization table che realizza un mapping many-to-one tra le cifre esadecimali e quelle decimali.

Il mapping many-to-one non è altro che una funzione suriettiva: ad ogni elemento del dominio corrisponde un solo ed unico elemento del codominio; ogni elemento del codominio è il corrispondente (l'immagine) di uno o più elementi del dominio.

Questa decimalization table si trova nell'HSM; in figura viene illustrata, a sinistra una tipica tavola di decimalizzazione e a destra una tavola che viene usata per sferrare un attacco:

 Tavole di decimalizzazione tradizionale e d'attacco

La tavola di decimalizzazione non è considerata un input sensibile da molti HSM, così le API di questi prevedono l'inserimento, oltre che del numero di conto bancario e del PIN, di una tavola di decimalizzazione del tutto arbitraria. Manipolando la tavola, ad ogni tentativo di inserimento di un PIN, è possibile apprendere molto sul valore corretto del PIN. Ad esempio, sostituiamo la decimalization table con la tavola sulla destra ed utilizziamo un PIN di prova 0000;

interrogando l'API si può sapere se il numero 7 esista o no nel PIN originale.

4.2 Generazione del PIN e tecniche di verifica

Esistono numerose tecniche per la generazione e la verifica del PIN. 

Il nostro obiettivo è analizzare in maggiori dettagli il metodo IBM 3624-Offset in quanto caratterizzato dall'uso di tavole di decimalizzazione.

Il metodo di generazione del PIN cliente dell’IBM 3624-Offset

Il metodo IBM 3624-Offset, sviluppato per la prima generazione dei bancomat, è stato molto adoperato e imitato.

Viene adottato uno schema in cui i PIN degli utenti possono essere calcolati dal numero di conto bancario dell' utente stesso cifrandolo con una chiave segreta ( mediante cifratura DES ). Il numero di conto è reso disponibile su scheda magnetica, quindi la macchina adibita all'erogazione del denaro necessita solo di un modo sicuro per immagazzinare la singola chiave utilizzata per la cifratura.

Il numero di conto è rappresentato con cifre ASCII e può essere interpretato come un input esadecimale per il cifrario a blocchi DES.

Dopo la codifica con la "chiave di generazione del PIN" segreta, l'output è convertito in esadecimale e tutte le cifre, tranne le prime quattro, vengono scartate. Le quattro cifre esadecimali sono poi convertite in cifre decimali utilizzando il mapping secondo la decimalization table. Infine per permettere all'intestatario della carta bancomat di cambiare il proprio PIN, viene addizionato un offset al quartetto decimale ottenuto in precedenza (l'offset è pubblico e varia a seconda delle banche). Quando un bancomat verifica un PIN inserito, semplicemente sottrae l'offset e confronta il risultato ottenuto con il PIN naturale, ossia il quartetto ottenuto dal processo descritto precedentemente, partendo dal numero di conto fornito dalla carta magnetica.

Esempio

N° di conto:             4556 2385 7753 2239

        -- Cifratura DES --

N° di conto cifrato:     3F7C 2201 00CA 8AB3

        -- Scarto cifre non usate --

1° quartetto del N°c.c.: 3F7C

        -- Mapping --

           0 1 2 3 4 5 6 7 8 9 A B C D E F

           0 1 2 3 4 5 6 7 8 9 0  1  2 3  4 5

PIN naturale:             3572

Offset pubblico:         4344

        -- PIN naturale + Offset pubblico --

PIN del cliente:          7916

API dei moduli di sicurezza hardware

I bancomat e i centri di controllo delle banche usano l'HSM (Hardware Security Module), un coprocessore che svolge servizi di crittografia e sicurezza, per proteggere le chiavi scelte per cifrare i PIN da impiegati corrotti e attaccanti. Una tipica API finanziaria ha funzioni per generare e verificare i PIN, funzioni per tradurre i PIN adottando diverse chiavi di cifratura quando questi viaggiano tra banche differenti, e altre importanti funzioni gestionali.

Tipicamente chiunque abbia accesso al computer HSM, secondo le politiche d'uso, può effettuare ogni giorno comandi come la verifica di un PIN, mentre funzioni sensibili come il settaggio di nuove chiavi di cifratura, possono essere effettuate solo con l'autorizzazione da parte di più impiegati fidati.

Nella figura viene riportato un prototipo di funzione per la verifica del codice PIN di prova. 

La funzione prende in input i seguenti parametri: il PAN_data, ovvero il numero di conto, la tavola di decimalizzazione e l'encrypted_PIN_block. I primi due dati vengono immessi in chiaro e possono essere manipolati con relativa facilità da un attaccante; l'ultimo dato, un PIN cifrato, che rappresenta un PIN di prova scelto per l'attacco, è più difficile da ottenere.

 Figura 4.2: Codice del prototipo della funzione per la verifica di un PIN di prova cifrato.

Oltre ai parametri di input, su citati, tutti gli altri dati presenti nella funzione "Encrypted_PIN_Verify" dipendono dal sistema informatico della banca, quindi non dovrebbero interessare un ipotetico attaccante. Come si può notare anche dai commenti in figura, questi dati sono le chiavi di cifratura, il formato del PIN_block, il tipo del metodo di verifica da usare, il numero di cifre che compongono il codice PIN e l'offset.

Gli altri valori sono delle costanti (A_RETRES e A_ED) rappresentanti gli outputs della funzione, ossia i codici 0 o 4,19 corrispondenti rispettivamente a una risposta affermativa e negativa alla richiesta di verifica. 

Come notato, il PIN dato in input alla funzione di verifica è in forma cifrata; quindi a un attaccante non è possibile inserire il PIN di prova in chiaro. 

Alcuni HSM, tuttavia, permettono l'inserimento in chiaro dei PIN di prova. Questa funzionalità può essere richiesta per inserire PIN di prova casuali quando si vogliono generare PIN cifrati per gli schemi che non utilizzano tabelle di decimalizzazione. L'appropriato comando è Clear_PIN_Encrypt, che, dal PIN in chiaro inserito, genera un PIN cifrato. Si noti che abilitando questo comando si corrono altri rischi oltre a quello di permettere l'attacco con tavole di decimalizzazione. Se non viene effettuato il padding randomizzato dei PIN prima che essi vengano cifrati, un attaccante può costruirsi un elenco di PIN di prova cifrati noti, confrontare ogni PIN cifrato prelevato dai pacchetti in transito verso l'HSM con quelli dell'elenco e determinarne il valore.

4.3 Attacchi alle tavole di decimalizzazione

Schema di base

Lo schema di base di un attacco a una tavola di decimalizzazione è diviso in due fasi. Nella prima fase vengono determinate quali cifre sono presenti nel PIN da ricercare. Nella seconda fase sono testati tutti i PIN composti con le cifre identificate.

Sia Dorig la tavola di decimalizzazione iniziale.

Per una data cifra decimale i, consideriamo una tavola di decimalizzazione binaria Di in cui compare 1 alla posizione x se e solo se Dorig ha i in quella posizione.

In altre parole,

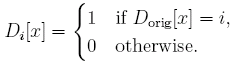
Per esempio, per una tavola standard Dorig = 0123 4567 8901 2345, utilizzando la formula in  figura, il valore di D₃ è 0001 0000 0000 0100.

Nella prima fase, per ogni cifra i, testiamo il PIN originale con una tavola di decimalizzazione Di e un PIN di prova 0000. E' semplice constatare che il test fallisce quando il PIN originale contiene la cifra i. Così, utilizzando al massimo dieci tentativi, determiniamo quali sono le cifre del PIN originale.

Nella seconda fase, proviamo tutte le possibili combinazioni di queste cifre. Il loro numero dipende da quante cifre differenti il PIN contiene.

CIFRE      POSSIBILITA'

A               AAAA(1)

AB            ABBB(4),   AABB(6),   AAAB(4)

ABC         AABC(12), ABBC(12), ABCC(12)
ABCD      ABCD(24)

Guardando la tabella:

nella prima riga AAAA(1) indica che esiste una sola combinazione quando abbiamo un' unica cifra;

nella seconda riga AABB(6) indica che esistono sei combinazioni quando abbiamo due cifre diverse che compaiono due volte ognuna; e cosi di seguito...

La tabella mostra che la seconda fase richiede al più 36 tentativi (quando il PIN originale contiene 3 cifre differenti), con un totale di 46 tentativi tra le due fasi, nel caso peggiore.

Schema adattivo

Il processo di craking di un PIN può essere rappresentato con un albero di ricerca. Ogni nodo v contiene un test in cui vengono specificati una tavola di decimalizzazione D_v e un PIN di prova p_v. Partiamo dalla radice dell'albero di ricerca e percorriamo i cammini possibili verso le foglie, determinando i risultati dei nostri test. Sia p_orig il PIN originale, ossia un codice di quattro cifre esadecimali. A questo quartetto viene applicato il mapping specifico della tabella di decimalizzazione, quindi ad ogni nodo confrontiamo se D_v(p_orig) = p_v, quindi ci spostiamo a destra se l'uguaglianza è verificata, a sinistra se non lo è.

Ogni nodo v nell'albero può essere associato ad una lista P_v di potenziali PIN originali tale che p Є P_v se e solo se v è raggiunto nel processo descritto in precedenza.

In particolare la lista P_v associata al nodo radice contiene tutti i possibili PIN, mentre le liste associate ai nodi foglia sono formate da un solo elemento: un PIN originale p_orig.

Consideriamo l'esempio seguente, rappresentato nella  figura 4.3. Per semplicità assumiamo che il PIN originale sia composto da due differenti cifre binarie e che la tavola di decimalizzazione Dorig sia uguale a 01. La tavola di decimalizzazione binaria Di  (ove per i = 0 oppure 1), in questo caso, corrisponde a D_xy .

 Quindi D_xy  denota la tavola di decimalizzazione che mappa 0 ==> x e 1 ==> y. 

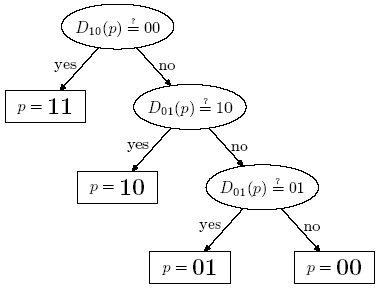
     Figura 4.3: Albero di ricerca per lo schema di base 

Come si può notare dalla figura se, ad esempio, si verifica il test D₁₀ (p) = 00, allora p = 11.

Questo avviene perchè, al PIN originale p si applica il mapping  1 ==> y (ossia 1 ==> 0). Se, invece, il test D₁₀ (p) = 00 non risulta vero, allora il PIN originale p contiene la cifra 0 e di conseguenza vengono considerati come PIN di prova 01 e 10, mentre l' altra possibile tavola D_xy da considerare, oltre D₁₀ , è D₀₁ . 

Lo svantaggio maggiore di questo schema è che il numero di tentativi richiesto dipende strettamente dal PIN originale p_orig. Ad esempio, il metodo di base necessita di al più 9 tentativi per p_orig = 9999 (dopo aver identificato quali sono le cifre decimali presenti nel PIN non c'è bisogno di far altro, dato che 9999 è l'unico PIN che può essere costruito con quattro cifre tutte uguali a 9), ma esistono casi in cui sono richiesti fino a 46 tentativi e di conseguenza l'albero di ricerca che si ottiene è molto sbilanciato e quindi non ottimale.

Un modo per produrre un perfetto albero di ricerca è considerare tutti gli alberi di ricerca possibili e scegliere quello migliore. Purtroppo quest'approccio è proibitivo a causa della sua complessità computazionale esponenziale rispetto al numero di possibili PIN e di tavole di decimalizzazione. Decidiamo dunque di rimpiazzare la ricerca esaustiva dell'albero di ricerca con una semplice euristica.

Scegliamo i valori di D_v e di p_v per ogni nodo v nel seguente modo. Sia P_v la lista associata al nodo v. Consideriamo tutte le possibili coppie di D_v e p_v e scegliamo quella per cui la probabilità di D_v(p) = p_v, (ove  p Є P_v), è vicina ad ½ il più possibile. Questo assicura che il sottoalbero di sinistra e quello di destra siano approssimativamente della stessa dimensione così che l'intero albero sia bilanciato.

Ricordiamo che il PIN originale p_orig è un numero esadecimale di 4 cifre ma quello che a noi interessa è p = Dorig(p_orig) che è un numero di quattro cifre decimali.

Ad esempio, utilizzando la tavola di decimalizzazione tradizionale, non distinguiamo tra 012D e ABC3 perché entrambi hanno p = 0123. Può essere facilmente dimostrato che è possibile costruire alberi di ricerca basati sul valore di p anziché sul valore di p_orig utilizzando tavole D_v che non distinguono tra 0 ed A, 1e B, 2 e C, 3 e D, 4 ed E, 5 ed F. Quindi chiediamo che ogni D_v soddisfi la proprietà che per ogni coppia di cifre esadecimali (x,y) tale che 

D_orig[x] = D_orig[y] deve implicare che D_v[x] = D_v[y]. Questa proprietà ci permette di ridurre il numero di possibili PIN da 16⁴ = 65536 a 10⁴ = 10000.

La seguente figura mostra esempi di outputs forniti dall'algoritmo appena descritto per il PIN originale p_orig = 3491 (tenendo presente che la tavola D_orig non è nota, quindi non sappiamo con precisione a quali cifre decimali corrispondono gli '1' presenti nella tavola D_v ).

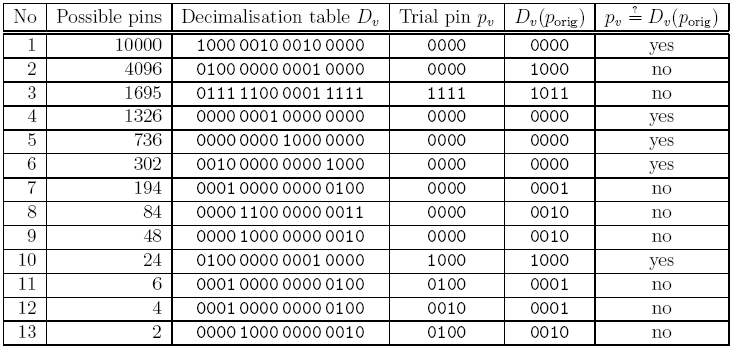
 Figura 4.4:   Esempio di output per un programma basato sullo schema adattivo.

Schema adattivo del PIN Offset

Quando l'attaccante non conosce nessun PIN di prova criptato e non può criptare i propri tentativi, può aver successo manipolando l'offset usato per la personalizzazione del PIN cliente.

Lo schema finale proposto è composto dalle stesse due fasi dello schema di base, quindi il primo compito è determinare quali cifre sono presenti nel PIN.

Assumiamo che sia stato intercettato un pacchetto in cui il campo del PIN criptato contiene un PIN valido per un conto e per semplicità assumiamo che il titolare del conto non abbia cambiato il suo PIN e l'offset corretto sia 0000.

Utilizzando il seguente insieme di tavole di decimalizzazione, l'attaccante può determinare quali cifre sono presenti nel PIN corretto.

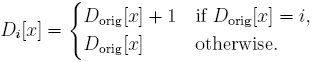
Ad esempio, per la tavola D_orig = 0123 4567 8902 3456, il valore di D₃ è 0124 4567 8901 2445. Supponiamo che il PIN criptato e la tavola di decimalizzazione forniti siano ogni volta quelli corretti.

Come nello schema di base, la seconda fase determina le posizioni delle cifre presenti nel PIN. Consideriamo il caso comune in cui abbiamo un PIN con tutte le cifre differenti, 1583 ad esempio. Possiamo provare a determinare la posizione della cifra 8 applicando un particolare offset e facendo dei test.

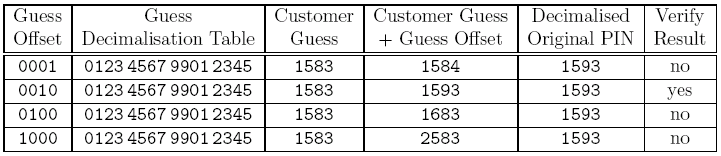
Gli offset che utilizziamo sono 0001, 0010, 0100, e 1000.

Ognuno di questi offset mappa un PIN valido (prelevato in precedenza dal pacchetto intercettato) in un nuovo PIN che può o non può combaciare con il PIN originale dopo che esso è stato decimalizzato, utilizzando la tavola di decimalizzazione modificata. (Il mapping avviene sommando in decimale il valore dell'offset con il PIN valido).

Se il PIN valido sommato all'offset è uguale al PIN originale decimalizzato allora la verifica del PIN restituisce "Yes" altrimenti "No". 

Questa procedura viene ripetuta fino a quando non è nota la posizione di tutte le cifre.

Nel caso di un PIN che ha tutte le cifre differenti, sono richiesti 6 tentativi per determinare la giusta posizione delle cifre.

Ecco uno schema riassuntivo del numero massimo di tentativi per determinare la giusta posizione delle cifre:

CIFRE                        N° TENTATIVI (MAX.)

TUTTE UGUALI                   1

2 DIFFERENTI                    13

3 DIFFERENTI                     9
TUTTE DIFFERENTI           6

4.4 Risultati

Utilizzando l'algoritmo con schema adattivo del PIN Offset, la distribuzione dei tentativi richiesti per l'individuazione dei PIN è rappresentata dal seguente grafo. Il grafo rappresenta il numero di PIN, che possono essere individuati, corrispondente a un preciso numero di tentativi.

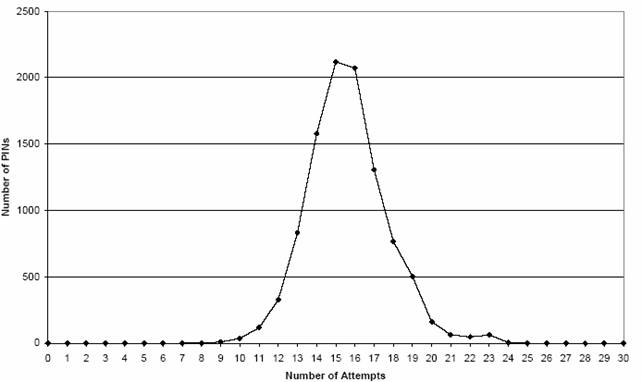
Possiamo notare che con solo 14-15 tentativi, in media, si possono trovare oltre 2000 codici PIN.

Facendo un confronto con l'attacco base, notiamo che, con lo schema adattivo del PIN Offset, il numero di tentativi per individuare un PIN, nel caso medio (caso in cui il PIN ha solo 2 cifre diverse) scendono da 24 a 15. 

Gli attacchi sono stati effettuati con successo riuscendo ad estrarre i PIN generati col metodo IBM 3624.