Cicli in CFG (Control Flow Graph)
Definiamo cosa costituisce un
ciclo in un CFG [1].
Dobbiamo usare la nozione di nodo dominante
un altro per definire i cicli naturali e l’importante classe di CFG riducibili.
Nodi dominanti
Diremo che il nodo d di un
CFG domina n, scritto d dom n, se ogni percorso dal nodo
iniziale del CFG fino a n passa attraverso d. Quindi, ogni nodo domina se
stesso, e il punto d’ingresso di un ciclo domina tutti i nodi nel ciclo.
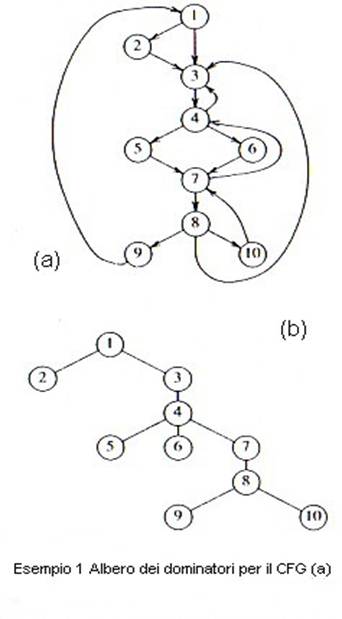
Esempio 1.
Consideriamo il CFG nella Fig.1 con nodo iniziale 1. Il nodo iniziale domina
ogni nodo. Il nodo 2 domina solo se stesso, perché il controllo può raggiungere
ogni altro controllo solo attraverso un percorso che
inizia per 
.
Il nodo 3 domina tutto tranne
1 e 2. Il nodo 4 domina tutto tranne 1, 2 e 3, mentre
tutti i percorsi che partono da 1 devono iniziare 
oppure 
. I nodi 5 e 6 dominano solo se stessi, perché il flusso di
controllo può saltare uno dei due passando attraverso l’altro. Infine, 7 domina
7, 8, 9, 10; 8 domina 8, 9, 10; 9 e 10 dominano solo se stessi.
Un modo utile di presentare
le informazioni sui dominatori è di usare un albero, chiamato albero
dei dominatori, in cui il nodo iniziale è la radice, e ogni nodo d
domina solo i suoi discendenti nell’albero. Nell’esempio 1 è mostrato l’albero
di dominazione per il CFG in figura.
L’esistenza di alberi di dominazione è una conseguenza di una proprietà
dei dominatori; ogni nodo n ha un unico dominatore immediato m che è l’ultimo dominatore di n su qualunque percorso dal nodo iniziale fino
a n. In termini della relazione dom,
il dominatore immediato m ha la proprietà che se 
e d dom n, allora d dom m.
Cicli naturali
Un’importante applicazione delle
informazioni sui dominatori sia ha nella determinazione dei cicli in un CFG
usato per il perfezionamento. Ci sono due proprietà essenziali di questi cicli:
1 - Un ciclo deve avere un
unico punto d’accesso, chiamato “header”. Questo punto d’accesso domina
tutti i nodi nel ciclo, oppure potrebbe non essere il solo punto d’ingresso nel
ciclo.
2 – Deve esserci almeno un
modo per iterare il ciclo (almeno un percorso all’indietro verso l’header).
Un buon modo per trovare
tutti i cicli in un CFG è di cercare gli archi nel CFG le cui teste dominano le
loro code. (Se 
è un arco, b è la testa e a è la coda) .
Chiameremo questi archi “archi
all’indietro”.
Esempio 2 .Nella
figura dell’esempio 1 c’è un arco 
, e 4 dom 7. Analogamente, 
è un arco, e 7 dom 10. Gli altri archi con questa proprietà
sono 
, 
, e 
. Notiamo che questi sono esattamente gli archi che formano i
cicli nel CFG.
Dato un arco all’indietro 
,
definiamo il ciclo naturale dell’arco come il nodo b più l’insieme dei nodi
che possono raggiungere n senza passare per b.
Esempio 3.
Il ciclo naturale dell’arco 
consiste dei nodi 7, 8 e 10, poiché 8 e 10 sono tutti quei
nodi che possono raggiungere 10 senza passare per 7. Il ciclo naturale
dell’arco 
consiste dell’intero insieme dei nodi (ma anche dai nodi che formano il percorso 
).
CFG riducibili
I grafi di flusso che si
presentano in pratica frequentemente rientrano nella classe dei CFG riducibili
definiti di seguito.
L’esclusivo uso di costrutti
strutturati per il controllo del flusso come if-then-else, while-do, continue, e
break producono programmi i cui grafi di flusso sono sempre riducibili. Perfino
i programmi scritti usando il costrutto goto sono di solito riducibili.
Sono state proposte una gran
varietà di definizioni di “CFG riducibili”. Quella che adottiamo qui mette in
evidenza una delle più importanti proprietà dei CFG riducibili; in altre
parole, non ci sono salti verso un punto interno del ciclo provenienti
dall’esterno; l’unico modo per entrare in un ciclo è attraverso il suo header.
Un CFG G è riducibile se e solo se possiamo partizionare gli archi in due
gruppi disgiunti, spesso chiamati archi in avanti e archi all’indietro, aventi
le seguenti proprietà:
1. Gli archi
in avanti formano un grafo aciclico in cui ogni nodo può essere
raggiunto dal nodo
iniziale di G.
2. Gli archi
all’indietro consistono solo di archi le cui teste dominano le loro
code.
Esempio 4.
Il CFG dell’esempio 1 è riducibile. In generale, se conosciamo la relazione dom per un CFG, possiamo trovare e
rimuovere tutti gli archi all’indietro. Gli archi rimanenti devono essere gli
archi in avanti se il grafo è riducibile,
e per controllare se un CFG è riducibile è sufficiente controllare che
gli archi in avanti formino un grafo aciclico. Nel caso del nostro esempio, è
facile verificare che se rimuoviamo i cinque archi all’indietro 
, 
, 
, 
, e 
, le cui teste dominano le loro
code, il grafo rimanente è aciclico.
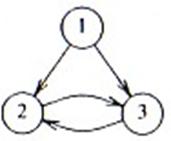
Esempio 5.
Consideriamo il CFG nella figura, il cui nodo iniziale è 1. Questo CFG non ha
archi all’indietro, perché nessuna testa di un arco domina la coda di
quell’arco. Quindi, potrebbe essere riducibile solo se l’intero grafo fosse
aciclico. Ma siccome non lo è, il CFG non è riducibile. Intuitivamente, la
ragione per cui questo CFG non è riducibile è che nel ciclo 
si può entrare in due
punti distinti, al nodo 2 e al nodo 3.
La proprietà chiave dei CFG
riducibili per l’analisi dei cicli è che in tali grafi di flusso, ogni insieme
di nodi che vogliamo considerare come ciclo deve contenere un arco
all’indietro. Infatti, dobbiamo esaminare solo i cicli naturali degli archi
all’indietro in modo da trovare tutti i cicli in un programma il cui grafo di flusso
è riducibile.
Al contrario, il grafo di
flusso del nostro esempio sembra avere un ciclo consistente dai nodi 2 e 3, ma
non c’è un arco all’indietro per cui questo sia un ciclo naturale. Infatti, il
ciclo ha due header, 2 e 3, che rende
inutilizzabili molte tecniche di ottimizzazione utilizzate dai compilatori.
Fortunatamente, i CFG non
riducibili compaiono molto raramente nei programmi tanto da rendere di
secondaria importanza lo studio di cicli con più di un header.
Ci sono linguaggi, come Bliss
and Modula. 2, che permettono solo programmi con CFG riducibili, e molti altri
linguaggi che produrranno CFG riducibili se usiamo il goto.