Le chiavi usate durante i vari round sono estratte dalla chiave k che noi stabiliamo. Ricordiamo che k è una chiave di 64 bit di cui 8 utilizzati per il controllo di parità. Tali bit sono quelli in posizione 8, 16, 24, ..., 64 e sono tali che ogni byte della chiave contenga un numero dispari di bit 1. Ciò significa che solo un errore può essere rivelato in ogni byte.

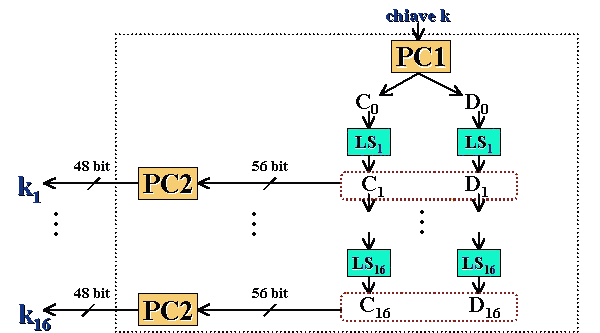
Vediamo ora più precisamente come vengono ricavate le chiavi usate durante le iterazioni (Figura 2.5.1).
Data una chiave k di 64 bit, non consideriamo gli 8 bit di parità e permutiamo i rimanenti 56 bit tramite la permutazione PC-1 riportata in figura 2.5.2. Sia PC-1(k) = C0D0 dove C0 e D0 sono i primi e gli ultimi 28 bit di PC-1(k).
Per 1 £ i £ 16 computiamo
Ci = LSi(Ci-1);
Di = LSi(Di-1);
Ki = PC-2(CiDi)
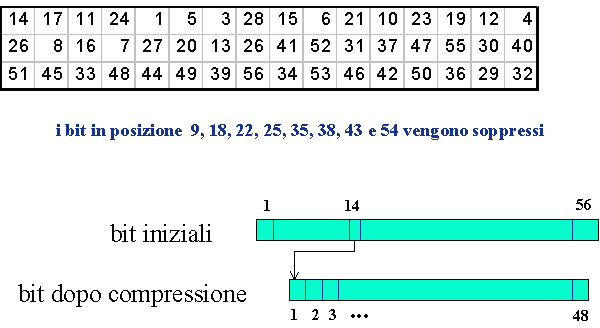
dove LSi è uno shift ciclico a sinistra di una o due posizioni a seconda del valore di i (lo shift riguarda una sola posizione alle iterazioni 1, 2, 9 e 16, e due posizioni a tutte le altre iterazioni). PC-2 rappresentata in figura 2.5.3 è una compressione di una stringa di input a 56 bit, in una stringa di output a 48 bit.

Osserviamo che i bit che vengono soppressi dalla compressione sono quelli in posizione 9, 18, 22, 25, 35, 38, 43 e 54 della stringa input. Tutto il procedimento di questo algoritmo è noto (in quanto pubblicato già da una ventina di anni) e chiunque volendo può seguirlo per effettuare cifrature; l'unica cosa che viene nascosta è il valore della chiave iniziale k.