
|
|
|
|
Il
primo algoritmo della rassegna può essere considerato il capostipite di una
generazione, MD4 fu introdotto da Ron Rivest nel 1990, le prime 2 lettere del
nome sono: MD la sigla di message digest, il
termine che in letteratura viene usato per indicare l'output di un algoritmo
di
hashing.
Le caratteristiche salienti di MD4 sono: velocità, compattezza e
l'uso di tabelle di memorizzazione di ridotte dimensioni, purtroppo non è
sicuro.
L'algoritmo richiede che sia soddisfatto un piccolo insieme di
condizioni preliminari: è scritto per architetture di tipo little-endian, con
parole di 32 bit, la lunghezza massima dell'input è 264 bit, il
valore hash restituito ha dimensione 128 bit.
Di seguito viene
riportato un breve glossario dei termini usati:
Parola macchina o parola: unità di misura della unità della macchina sottostante corrispondente a 32 bit.
Little-endian: Supponiamo di avere una parola
macchina a 32 bit, questa sarà composta da
4 byte, indichiamoli con
b1,b2,b3,b4, il valore numerico
della parola sarà dato da: b4224 + b3216
+b228+b1.
Big-endian: La situazione è identica a quella
suddetta,
ma il valore numerico sarà dato da: b1224 +
b2216+b328+b4.
MD4 può essere
diviso nei seguenti 4 passi,di cui 3 preparano l'input per l'elaborazione che
viene effettuata nel quarto:
Concatenazione del
padding
Il messaggio originale X viene esteso con un singolo bit 1 e un
numero appropriato di bit 0 che rendono la
lunghezza congruente a 448 (mod 512), se la lunghezza originale era già
congruente, vengono comunque aggiunti altri 512 bit, perciò in questo passo
vengono aggiunti un numero di caratteri compresi fra 1 e 512, a questo punto
mancano 64 bit per raggiungere una lunghezza multipla di 512 bit
Concatenazione
della lunghezza
Sia b la rappresentazione a 64 bit della lunghezza del
messaggio originale, b viene concatenato alla stringa ottenuta al passo
precedente, il messaggio ottenuto che M ha una lunghezza multipla
di
512 e quindi anche di 16 parole.
La stringa di bit M verrà memorizzata in un vettore a n entrate ognuna della
dimensione di una parola, si ricorda che n è un multiplo di 16, M[i] con 1
![]() i
i ![]() n starà ad indicare li-esimo elemento
del
vettore. Le operazioni eseguiti in questi passi preliminari sono riassunte in figura 1:
n starà ad indicare li-esimo elemento
del
vettore. Le operazioni eseguiti in questi passi preliminari sono riassunte in figura 1:
|
|
|
|
Fig.1 Schema del padding
MD4 usa un buffer di 4 word (A, B, C, D) che viene inizializzato con le seguenti 4 costanti additive a 32 bit riportate in notazione esadecimale:
| h1 | h2 | h3 | h4 |
| 01234567 | 89abcdef | fedcba98 | 76543210 |
Fig,2 Costanti additive
Elaborazione del messaggio
Questo passo che rappresenta il
cuore dell'algoritmo è diviso in 3 round, ognuno dei quali svolge 16
operazioni,
ognuno dei round usa 1 sola delle 3 funzioni logiche che stanno per essere
definite:
| f(X,Y,Z) | G(X,Y,Z) | H(X,Y,Z) |
Fig.3 Funzioni logiche
La funzione f, usata nel I round ,
equivale
a if X then Y else Z, la funzione G, usata nel II round, è detta
maggioranza perché restituisce il valore di verità se almeno 2 delle 3
variabili
sono vere. Nel II e III round è fatto uso di 2 costanti numeriche esadecimali
a
32 bit che rappresentano la radice quadrata di 2 e di 3 (rispettivamente
5A827999 e 6ED9EBA1) , il I valore è usato durante il II round,
l'altro nel III, dora in poi le 2 costanti verranno indicate con ![]() . Le operazioni usate nell'algoritmo
sono:
. Le operazioni usate nell'algoritmo
sono:
·
Gli
operatori binari AND, OR, NOT.
·
L'addizione
intera,
modulo 232 .
·
L'operazione shift circolare sinistro <<.
Le
operazioni centrali dell'algoritmo sono:
t = ( A + F(B, C, D)+X[J] + y[J] )) << s[J]
(A,
B, C, D)=(D, T, B, C)
I
valori di X[j] sono predefiniti e sono reperibili all'interno dell'algoritmo,
y[j] è la costante additiva relativa al round corrente, lo pseudo-codice per
l'algoritmo MD4 è:
ALGORITMO MD4
OPERAZIONE PRELIMINARE: IL PADDING Input:
Il messaggio M con | M | < 264 // Inizializza A, B, C, D usando
h1, h2, h3,
h4 for
i=0 to N/16-1 do for
j= 0 to 15 do X[j]= M[16i+j] AA= A
BB=B CC= C
DD=D //
Round 1 // ROund 2 //Round
3 output:
A || B || C || D |
 Lattacco ad MD4 richiede solamente pochi secondi usando un comune
PC e lascia una certa libertà sulla scelta del messaggio [5] . Si deduce facilmente che MD4 non è una funzione hash
resistente alle collisioni. Hans , a Spring nel 1996, ha trovato collisioni
anche per la funzione di compressione di MD5. L'attacco non è ancora stato
esteso a tutto l'algoritmo, a questo punto anche la resistenza di MD5
alle
collisioni, è seriamente messa in discussione. La RSA Data Security, ha
raccomandato di non usare più MD4, e per applicazioni future che richiedono
funzioni hash resistenti alle collisioni di non usare MD5. Da quanto detto
segue
che MD4 può essere usato solo come termine di paragone per lo studio
dell'evoluzione delle funzioni hash.
Lattacco ad MD4 richiede solamente pochi secondi usando un comune
PC e lascia una certa libertà sulla scelta del messaggio [5] . Si deduce facilmente che MD4 non è una funzione hash
resistente alle collisioni. Hans , a Spring nel 1996, ha trovato collisioni
anche per la funzione di compressione di MD5. L'attacco non è ancora stato
esteso a tutto l'algoritmo, a questo punto anche la resistenza di MD5
alle
collisioni, è seriamente messa in discussione. La RSA Data Security, ha
raccomandato di non usare più MD4, e per applicazioni future che richiedono
funzioni hash resistenti alle collisioni di non usare MD5. Da quanto detto
segue
che MD4 può essere usato solo come termine di paragone per lo studio
dell'evoluzione delle funzioni hash.
Md5 [8]
è basato su Md4
rispetto a quest'ultimo è più lento, ma più sicuro, le principali differenze
possono essere riassunte in:
Un IV round di 16 operazioni.
L'ordine d'accesso alle parole nei round 2 e 3.
Il numero delle operazioni di shift.
La
funzione del round 2 diventa
g(x,y,z)=
![]() .
.
Ad ogni passo è usata una costante additiva differente.
L'output del passo precedente è sommato al passo corrente.
Le operazioni
preliminari dell'algoritmo sono le stesse del md4, anche le costanti che vengono
inserite nei registri A, B, C, D sono identiche. Il IV round usa una nuova
funzione: k(x,
y, z) = ![]() . La funzione G, che calcolava la maggioranza dei 3 parametri
in input, è stata sostituita a causa della sua simmetria. La notazione, [abcd k s i] rappresenta
l'operazione:
. La funzione G, che calcolava la maggioranza dei 3 parametri
in input, è stata sostituita a causa della sua simmetria. La notazione, [abcd k s i] rappresenta
l'operazione:
a = b + ((a +
F(b,
c, d) + X[k] + T[i]) <<
s).
|
ALGORITMO MD5 OPERAZIONE PRELIMINARE: IL PADDING Input:
Il
messaggio M con
| M | < 264 // Inizializza A, B, C, D usando h1, h2, h3, h4 definite in MD4 A=
01234567
B= 89abcdef C=
fedcba98
D= 76543210 for
i=0 to N/16-1 do for j= 0 to 15 do X[j]=
M[16i+j] AA=A BB=B
CC=C
DD=D // Round 1 [ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4] // Round 2 [ABCD 1 5 17] [DABC 6 9 18] [CDAB 11 14 19] [BCDA 0 20 20] // Round
3 [ABCD 5 4 33] [DABC 8 11 34] [CDAB 11 16 35] [BCDA 14 23 36] // Round
4 [ABCD
0 6 49]
[DABC 7 10 50] [CDAB 14 15 51] [BCDA 5 21
52] Output:
A || B || C || D |
Lo
standard americano per l'hashing: SHS (Secure hashing standard) è una variante
di MD4 fu introdotto dal Nist nel 1993 e modificato nel 1994. L'algoritmo che
implementa lo standard è SHA (Secure hashing algorithm), la sua versione
modificata è: SHA-1. L'input è un messaggio M di lunghezza inferiore a
264 bit, e produce in output un messaggio X di 160 bit che
continueremo ad indicare come message digest. La prima operazione
dell'algoritmo
è il padding dell'input identico a quello eseguito in md4, alla stringa iniziale è
concatenato un singolo bit 1 e un numero opportuno di bit 0 in modo da rendere
la lunghezza multipla di 512, a questa nuova stringa è aggiunta la
rappresentazione binaria a 64 bit della lunghezza del messaggio originale
(vedi
MD4 per maggiori dettagli), per ottenere un digest di 160 bit sono usati 5
registri: A, B, C, D, E ognuno di 32 bit, lalgoritmo è definito per
architetture
di tipo big-endian.
Il messaggio M esteso può essere considerato come un vettore M(1),...,M(n)
dove
il singolo elemento è composto da gruppi di parole per 512 bit. Ci sono delle
funzioni logiche f0,..,f79 che lavorano su
gruppi di 3 word, ne sono definite 4 diverse nel seguente modo:
| Intervallo | Valore |
| 0..19 | |
| 20..39 | |
| 40..59 | |
| 60..79 |
Allo stesso modo delle funzioni viene definita una sequenza di costanti additive a 32 bit, indicate come C0,C1,..,C79:
| Intervallo | Valore |
| 0..19 | 5A827999 |
| 20..39 | 6ED9EBA1 |
| 40..59 | 8F1BBCDC |
| 60..79 | CA62C1D1 |
Differenze rispetto a md4:
Il message digest è lungo 160 bit, sono usati 5 registri di una parola, invece che 4. Sono eseguiti 4 round.
Ogni singolo blocco d'input (la cui dimensione è 512 bit, o 16 parole) è espanso alla dimensione di 80 parole, le nuove 64 parole sono ognuna definita come lo XOR di 4 parole precedenti.
Minore velocità.
Il passo di espansione nella sua versione revisionata introduce uno shift circolare di 1 posizione. L'operazione risultante è:
X[i] =( X[i-3] ![]() X[i-8]
X[i-8] ![]() X[i-14]
X[i-14] ![]() X[i-16] ) << 1
X[i-16] ) << 1
Dopo l'espansione
il
messaggio può essere visto come un insieme di n blocchi M(i) con 1
£ i
£
n , ognuno della
dimensione di 80 parole.
Il risultato della funzione è ottenuto mediante n
applicazioni dell'algoritmo riportato di seguito dove il risultato
dell'i-esimo
passo fa da vettore d'inizializzazione per l'(i+1)-esimo
passo:
|
ALGORITMO SHA-1 OPERAZIONE PRELIMINARE: IL PADDING Input: Il messaggio M
DOVE |M| < 264 // Passo despansione del messaggio
X[i]= (
X[i-3]
// Inizializzazione dei registri mediante vettore IV A= H0 B=
H1
C= H2 D=
H3
E= H4 // Passo centrale For i= 0
to 79 do Temp=( A
<< 5) + fi(B, C, D) + E + X[i] +
Ki //
Preparazione delloutput H0=
H0+A
H1= H1 + B H2
= H2+
C
H3 = H3 + D
H4= H4 + E Output:
H0 || H1 || H2 ||
H3 || H4
|
Gli algoritmi che abbiamo visto producono un valore hash di lunghezza
128
bit (MD4-MD5) e 160 bit (SHA-1) e permettono una sicurezza di 64 e 80 bit
rispettivamente, rispetto all'attacco del compleanno. Lo scopo del nuovo
Advanced Encryption Standard è stato quello di offrire alle variabili
crittografiche una sicurezza di 128, 192 e 256 bit. Questo ha costretto ad
apportare modifiche agli algoritmi hash in modo da ottenere tali livelli
di sicurezza. Così abbiamo nuovi algoritmi (SHA-256, SHA-512, SHA-384)
descritti
di seguito, che sono stati sviluppati e proposti nel Draft Federal Information
Processing Standard (FIPS)180-2 nel 2001 [10].
SHA-256 restituisce un valore hash di 256 bit e garantisce una
sicurezza
di 128 bit rispetto all'attacco del compleanno; SHA-512 restituisce un valore
hash di 512 bit e garantisce una sicurezza di 256 bit rispetto all'attacco del
compleanno; ed infine SHA-384 restituisce un valore hash di 384 bit e
garantisce
una sicurezza di 192 bit.
Descrizione generale: Opera nello stesso modo degli algoritmi MD4, MD5 e SHA-1. Processa il messaggio in blocchi di 512 bit. Ogni blocco consta di 16 parole da 32 bit. Prima di eseguire l'algoritmo vengono eseguite delle operazioni sul messaggio :
1.
padding: vengono aggiunti dei bit al messaggio in modo da ottenere una
lunghezza multipla di 512 bit;
2.
il messaggio viene suddiviso in blocchi di 512 bit: M(1), M(2),...,
M(N).
I
blocchi del messaggio sono processati uno ad uno, partendo da un fissato
valore
hash iniziale H(0) costituito da una sequenza di 8 parole di 32
bit.
Il valore hash viene
calcolato sequenzialmente mediante la seguente espressione:
H(i) = H(i-1) +
CM(i)
(H(i-1))
.
Dove C è la funzione di compressione di
SHA-256;
Descrizione di SHA-256: La funzione di compressione
di SHA-256 opera su blocchi di messaggio di 512 bit e su valori intermedi di
256
bit. Essa è essenzialmente un algoritmo cipher block di 256 bit, con valore di
input il valore hash intermedio e avente come chiave il blocco M(i) del
messaggio. Ci sono due importanti computazioni da descrivere:
Il valore d'inizializzazione H(0) è
costituito dalla seguente
sequenza di 8 parole di 32 bit:
|
H1(0) = 6a09e667 |
H2(0) = bb67ae85 |
H3(0) =
3c6ef372 |
H4(0) =
a54ff53a |
|
H5(0) = 510e527f |
H6(0) = 9b05688c |
H7(0) = 1f83d9ab |
H8(0) = 5be0cd19 |
In seguito il messaggio viene suddiviso in N blocchi di 512
bit:
I primi 32 bit del blocco i sono denotati con M0(i), i
successivi 32 bit con M1(i) e così di seguito fino a
M15(i).
Il calcolo del valore hash procede nel seguente
modo:
Sono utilizzate 6 funzioni logiche ognuna di
esse
opera su parole di 32 bit e produce un output di 32 bit. Le funzioni sono
definite come di seguito: Ch(X,
Y, Z) = (X
Maj(X,
Y, Z) = S0(X)
= S2(X)
S1(X)
= S6(X)
A0(X)
= S7(X)
A1(x)
= S17(X)
dove Rn = shift destro di n bit e Sn = rotazione
destra di n bit (per rotazione intendiamo uno shift ciclico sui
bit). Inoltre viene utilizzata la seguente sequenza di costanti k(0),
k(1),...,
k(63) a 32 bit: 428a2f98 71374491 b5c0fbcf e9b5dba5 3956c25b 59f111f1 923f82a4 ab1c5ed5 d807aa98 12835b01 243185be 550c7dc3 72be5d74 80deb1fe 9bdc06a7 c19bf174 e49b69c1 efbe4786 0fc19dc6 240ca1cc 2de92c6f 4a7484aa
5cb0a9dc
76f988da 983e5152 a831c66d b00327c8 bf597fc7 c6e00bf3 d5a79147 06ca6351 14292967 27b70a85 2e1b2138 4d2c6dfc 53380d13 650a7354 766a0abb 81c2c92e 92722c85 a2bfe8a1 a81a664b c24b8b70 c76c51a3 d192e819 d6990624 f40e3585 106aa070 19a4c116 1e376c08 2748774c 34b0bcb5 391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3 748f82ee 78a5636f 84c87814 8cc70208 90befffa a4506ceb bef9a3f7 c67178f2
Bisogna preparare il messaggio alla computazione. Supponiamo che la
lunghezza del messaggio sia L, aggiungiamo il bit 1 alla fine del messaggio e
k-zero bit dove k è ottenuta dall'equazione L+1+k=448 mod 512 infine viene
aggiunto un blocco di 64 bit. In questo modo la lunghezza del messaggio è un
multiplo di 512 bit. Ad esempio il messaggio di (8 bit ASCII) abc ha lunghezza
8*3=24 ad esso viene aggiunto un uno, 448-(24+1)=423 bit di zero e un blocco
di
64 bit in modo da ottenere una lunghezza di 512 bit.
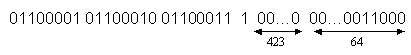
 Y)
Y)  (!X
(!X  Z)
Z)
(X
 Y)
Y)  (X
(X  Z)
Z)  (Y
(Y  Z)
Z)
 S13(X)
S13(X)  S22(X)
S22(X)
 S11(X)
S11(X)  S25(X)
S25(X)
 S18(X)
S18(X)  R3(X)
R3(X)
 S19(X)
S19(X)  R10(X)
R10(X)
| w(j)=Mj(i)
j=0, 1, 2, 3, 4,..., 15 and for j=16 to 63 |
graficamente:
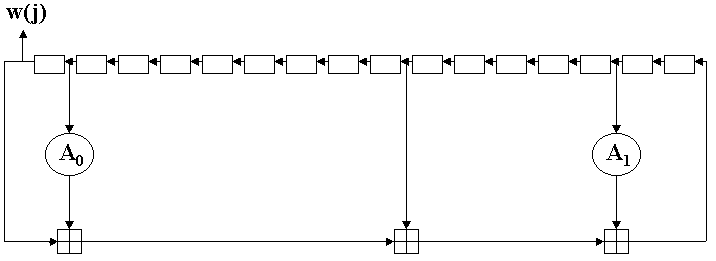
dove il simbolo ![]() denota l'addizione mod 232. Inizialmente i registri
(rappresentati graficamente dai 16 rettangolini) contengono le parole w(0),
w(1),..., w(15) nell'ordine da sinistra verso destra. Di volta in volta che
calcoliamo i nuovi valori w(j) per j=16,..., 63 i valori contenuti nei registri
sono shiftati di una posizione verso sinistra.
denota l'addizione mod 232. Inizialmente i registri
(rappresentati graficamente dai 16 rettangolini) contengono le parole w(0),
w(1),..., w(15) nell'ordine da sinistra verso destra. Di volta in volta che
calcoliamo i nuovi valori w(j) per j=16,..., 63 i valori contenuti nei registri
sono shiftati di una posizione verso sinistra.
Il
valore della funzione è ottenuto mediante l'esecuzione del seguente
algoritmo:
|
Ciclo principale (SHA-256)
a=H1
(i-1) For j=0 to 63{
|
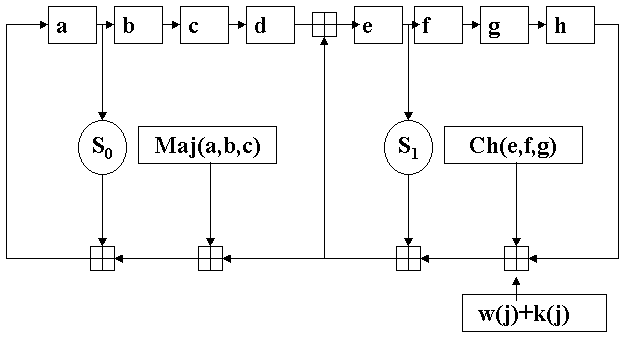
La funzione di compressione è così rappresentata:
Descrizione generale: E' una variante di
SHA-256.
Processa il messaggio in blocchi di 1024 bit. Ogni blocco consta di 16 parole
da
64 bit. Prima di eseguire l'algoritmo vengono eseguite delle operazioni sul
messaggio :
I blocchi di messaggio sono processati uno ad uno,
partendo da un
fissato valore hash iniziale H(0), costituito da 8 parole di 64
bit.
Il valore hash viene calcolato sequenzialmente mediante la seguente
espressione:
H(i) = H(i-1) + CM(i)(H
(i-1))
Dove C è la
funzione di compressione di
SHA-512
Il valore d'inizializzazione H(0) è
costituito dalla
seguente
sequenza di parole di 64 bit:
|
H1(0) = 6a09e667f3bcc908 |
H2(0) = bb67ae8584caa73b |
H3(0) =
3c6ef372fe94f82b |
H4(0) =
a54ff53abf1d36f1 |
|
H5(0) = 510e527fade682d1 |
H6(0) = 9b05688c2b3e6c1f |
H7(0) = 1f83d9abfb41bd6b |
H8(0) = 5be0cd19137e2179 |
Bisogna preparare il messaggio alla computazione. Supponiamo che la
lunghezza del messaggio sia L, aggiungiamo il bit 1 alla fine del messaggio e
k-zero bit (dove k è ottenuta dall'equazione L+1+k=896 mod 1024) ed infine
aggiungiamo un blocco di 128 bit. In questo modo la lunghezza del messaggio è
un
multiplo di 1024. Ad esempio il messaggio di (8 bit ASCII) abc ha lunghezza
8*3=24 ad esso viene aggiunto un uno, 896-(24+1)=871 zero bit, e un blocco di
128 bit in modo da ottenere una lunghezza di 1024 bit.
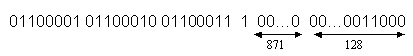
In seguito il messaggio viene diviso in N blocchi di
1024 bit:
Il calcolo del valore hash procede nel seguente
modo: Sono utilizzate 6 funzioni logiche.
Ognuna di tali
funzioni opera su parole di 64 bit e produce un output di 64 bit. Le funzioni
sono definite come di seguito: Ch(X,
Y, Z) = (X
Maj(X,
Y, Z) = S0(X)
= S(X)28
S1(X)
= S14(X)
A0(X)
= S7(X)
A1(x)
= S19(X)
Inoltre è utilizzata la
seguente sequenza di
costanti k(0), k(1),..., k(79): 428a2f98d728ae22 7137449123ef65cd b5c0fbcfec4d3b2f
e9b5dba58189dbbc 3956c25bf348b538 59f111f1b605d019 923f82a4af194f9b ab1c5ed5da6d8118 d807aa98a3030242 12835b0145706fbe 243185be4ee4b28c 550c7dc3d5ffb4e2 72be5d74f27b896f 80deb1fe3b1696b1 9bdc06a725c71235 c19bf174cf692694 e49b69c19ef14ad2 efbe4786384f25e3 0fc19dc68b8cd5b5 240ca1cc77ac9c65 2de92c6f592b0275 4a7484aa6ea6e483 5cb0a9dcbd41fbd4 76f988da831153b5 983e5152ee66dfab a831c66d2db43210 b00327c898fb213f bf597fc7beef0ee4 c6e00bf33da88fc2 d5a79147930aa725 06ca6351e003826f 142929670a0e6e70 27b70a8546d22ffc 2e1b21385c26c926 4d2c6dfc5ac42aed 53380d139d95b3df 650a73548baf63de 766a0abb3c77b2a8 81c2c92e47edaee6 92722c851482353b a2bfe8a14cf10364
a81a664bbc423001 c24b8b70d0f89791 c76c51a30654be30 d192e819d6ef5218 d69906245565a910 f40e35855771202a 106aa07032bbd1b8 19°4c116b8d2d0c8 1e376c085141ab53 2748774cdf8eeb99 34b0bcb5e19b48a8 391c0cb3c5c95a63 4ed8aa4ae3418acb 5b9cca4f7763e373 682e6ff3d6b2b8a3 748f82ee5defb2fc 78a5636f43172f60 84c87814a1f0ab72 8cc702081a6439ec 90befffa23631e28 a4506cebde82bde9 bef9a3f7b2c67915 c67178f2e372532b ca273eceea26619c d186b8c721c0c207 Eada7dd6cde0eb1e f57d4f7fee6ed178 06f067aa72176fba
0a637dc5a2c898a6
113f9804bef90dae 1b710b35131c471b 28db77f523047d84
32caab7b40c72493 3c9ebe0a15c9bebc 431d67c49c100d4c 4cc5d4becb3e42b6
597f299cfc657e2a 5fcb6fab3ad6faec 6c44198c4a475817.
I primi
64 bit del
blocco i sono denotati con M0(i), i successivi 64 bit con
M1(i) e così di seguito fino a M15(i).
 Y)
Y)  (!X
(!X  Z)
Z)
(X
 Y)
Y)  (X
(X  Z)
Z)  (Y
(Y  Z)
Z)
 S34(X)
S34(X)  S30(X)
S30(X)
 S18(X)
S18(X)  S41(X)
S41(X)
 S8(X)
S8(X)  R7(X)
R7(X)
 S61(X)
S61(X)  R6(X)
R6(X)
| w(j)=Mj(i)
j=0, 1, 2, 3, 4,..., 15 and for j=16 to 79 |
graficamente:

dove il simbolo ![]() denota l'addizione mod 264. Inizialmente i registri
(rappresentati graficamente dai 16 rettangolini) contengono le parole w(0),
w(1),..., w(15) nell'ordine da sinistra verso destra. Di volta in volta che
calcoliamo i nuovi valori w(j) per j=16,..., 63 i valori contenuti nei registri
sono shiftati di una posizione verso sinistra.
denota l'addizione mod 264. Inizialmente i registri
(rappresentati graficamente dai 16 rettangolini) contengono le parole w(0),
w(1),..., w(15) nell'ordine da sinistra verso destra. Di volta in volta che
calcoliamo i nuovi valori w(j) per j=16,..., 63 i valori contenuti nei registri
sono shiftati di una posizione verso sinistra.
Il
valore della funzione è ottenuto mediante l'esecuzione del seguente
algoritmo:
Ciclo principale (SHA-512)
a=H1
(i-1) For j=0 to 79{
La funzione di compressione è così rappresentata:
For i=1 to N {
Inizializzazione dei
registri
a,b,c,d,e,f,g,h con l'(i-1)esimo valore hash (uguale alle variabili
di inizializzazione se i=1)
-
-
-
b=H8 (i-1)
Calcolo delle funzioni:
Ch(e,f,g), Maj(a,b,c), S0(a) S1(e) e
w(j)
T1=
h+S1(e)+Ch(e,f,g)+k(j)+w(j)
T2=
S0(a)+Maj(a,b,c)
h=g
g=f
f=e
e=d+T1
d=c
c=b
b=a
a=T1+
T2
}
Calcolo
dell'i_esimo
valore hash intermedio H(i)
H1(i)= a +
H1(i-1)
H2(i)=
b +
H2(i-1)
-
-
-
H8(i)= h +
H8(i-1)
}
H(N)=(H1(N),
H2(N),... ,H8(N)) è il
valore
hash di M.

E'
definito nello stesso modo di SHA-512 con le seguenti differenze:
1. i
valori
di inizializzazione:
|
H1(0) = cbbb9d5dc1059ed8 |
H2(0) = 629a292a367cd507 |
H3(0) = 9159015a3070dd17 |
H4(0) = 152fecd8f70e5939 |
|
H5 (0) =
67332667ffc00b31 |
H6(0) =
8eb44a8768581511 |
H7(0) = db0c2e0d64f98fa7 |
H8(0)= 47b5481dbefa4fa4 |
|
|