CRITTOGRAFIA A CHIAVE PUBBLICA E CRITTOSISTEMA RSA 

1 - Crittografia a chiave pubblica

Il 1976 è un anno importante nella storia della crittografia moderna, non solo per la nascita del DES ma anche per l'introduzione di un nuovo concetto. Grazie a Diffie-Hellman e, indipendentemente, Merkle tale idea rivoluzionerà il modo di "comunicare in segreto": i cifrari a chiave pubblica.  L'impatto di questo nuovo nozione non fu immediato anche se poi risultò dirompente. Ci sono varie motivazioni, anche se in parte ancora oscure, del rifiuto iniziale nell’adozione di questo nuovo concetto. Diffie in un suo scritto è stato più che mai esplicito e molto critico, imputando la vera causa di tutto ciò ad una scelta "partigiana" della comunità e delle aziende che vedevano nel DES e nella produzione dei suoi "marchingegni hardware" un grosso business. Le stesse "bontà" commerciali non sembravano certe dal nuovo protocollo crittografico, cosicché il suo avvento venne soltanto rimandato, ma non fu possibile evitarlo data l'innovazione introdotta e le frontiere che potenzialmente si dischiudevano con questa nuova forma di crittografia. Infatti il cambiamento era indubbiamente radicale, vediamo di capire il perché.

1.1 - La chiave

I sistemi di crittografia a chiave pubblica, chiamati anche sistemi a due chiavi o asimmetrici, differiscono dai sistemi crittografici convenzionali perché non c'è più una singola chiave segreta condivisa da una coppia di utenti. Piuttosto, un generico utente A ha una propria chiave KA= (PA , SA), dove PA è la parte pubblica e SA è quella segreta. Le chiavi pubbliche vengono memorizzate in un file a cui tutti gli utenti del crittosistema possono accedere. La chiave pubblica PA effettua una trasformazione pubblica su un certo messaggio M generando il messaggio PA(M); mentre la chiave privata PB effettua una trasformazione privata generando il messaggio SA(M). Detto M l'insieme dei messaggi, le funzioni PA : M -> M e SA : M -> M sono definite, rispettivamente, funzioni di cifratura e decifratura. In tale sistema possiamo avere:

·         M = SA(PA(M))

·         M = PA(SA(M))

o entrambe le relazioni.

Uno dei requisiti di queste funzioni è che la funzione di decifratura deve essere del tipo "one­way". Una funzione è detta "one­way" quando è facile da calcolare ma difficile da invertire, sempre che non si ha un'informazione segreta aggiuntiva. Così, se SA(M) è una funzione di questo tipo, la decifratura da parte del crittoanalista è difficile da realizzare. Un esempio di funzione ritenuta "one­way" è: f(x) = xa mod n dove n è il prodotto di due primi p e q abbastanza grandi, a è un intero positivo ed f : Zn -> Zn .

1.2 - Sicurezza

Per garantire la sicurezza, le trasformazioni di un sistema a chiave pubblica devono soddisfare M = SA(PA(M)). Supponendo che A voglia spedire un messaggio in maniera sicura M a B. Allora:

·         A ottiene la chiave pubblica di B, PB;

·         A calcola il testo cifrato C = PB (M) corrispondente al messaggio M e lo spedisce a B;

·         B riceve il testo cifrato C e adopera la sua chiave privata SB per ottenere il messaggio M, SB (C) = SB (PB (M)) = M.

Nel caso in cui un nemico intercetti una trasmissione da A, certamente non può essere decifrata perché SB è privata, per questo motivo la sicurezza è garantita.

1.3 - Autenticità

Poiché tutti possono accedere a PB, B non può conoscere l'identità del mittente, perciò una trasmissione di A potrebbe essere alterata. Quindi per garantire autenticità ed integrità, le trasmissioni di un sistema a chiave pubblica devono soddisfare PA (SA (M)) = M. Supponiamo che A voglia mandare un messaggio autentico a B. Allora:

·         A calcola la sua firma digitale C’ = SA (M‘);

·         A spedisce la coppia (M ‘, C’) (messaggio, firma);

·         Quando B riceverà la coppia (M‘, C‘) può verificare che questo provenga da A essendo PA la chiave pubblica di A, verificando l'equazione M’ = PA (C’).

Così B può accertare che il messaggio è stato spedito da A e non è stato alterato. Infatti, assumendo che M’ è un testo in chiaro valido, B sa che C è stato spedito da A e non è stato alterato durante la trasmissione. Questo segue dalla natura ''one­way'' della funzione PA. Se un crittoanalista parte da un messaggio M' potrebbe trovare C' tale che PA (C') = M', questo implicherebbe che PA è invertibile, il che è un assurdo.

1.4 - Confronto con il crittosistema a chiave privata

Quindi il sistema a chiave pubblica presenta varie differenze rispetto al sistema a chiave privata. Nell'ambito della crittografia a chiave segreta si ha che:

Con la crittografia a chiave pubblica questi concetti subiscono una radicale modifica:

2 - Crittosistema RSA

Nel 1978 Rivest, Shamir e Adleman pubblicarono sulla famosa rivista "Communications of the ACM" la descrizione del cifrario RSA (dalle loro iniziali) che possedeva molte interessanti caratteristiche: costituiva il primo (insieme al cifrario di Merkle ed Hellman) esempio di cifrario a chiave pubblica; operava a blocchi interpretando ogni messaggio come un numero intero; la sua sicurezza si fondava sulla difficoltà della fattorizzazione di numeri interi molto grandi. Sebbene abbia attratto l'interesse di numerosi crittoanalisti, l'RSA rimane sino ad oggi sostanzialmente inviolato, e se a tutto ciò si aggiunge una grandissima semplicità strutturale, ecco che possiamo ben capire perché questo metodo di cifratura abbia avuto così tanto successo. Per la sua semplicità l'RSA è ampiamente utilizzato e numerose sono le sue realizzazioni in hardware presentate nel corso di questi anni. Si è detto che la sicurezza dell'RSA sia strettamente legata al problema della fattorizzazione, ma nessuno ha mai provato che questo legame significhi che i due problemi siano computazionalmente equivalenti. Comunque tutti gli sforzi fatti per rompere RSA hanno portato inevitabilmente ad individuare algoritmi per la fattorizzazione. D'altro canto, esistono delle varianti di RSA (Rabin, 1979) che sono dimostrativamente equivalenti al problema della fattorizzazione, e dunque ritenute più sicure almeno da un punto di vista matematico. Però queste varianti non sono semplici come RSA e quindi non hanno avuto il suo stesso successo.

2.1 - Algoritmo RSA

Generazione delle chiavi

Per generare la chiave pubblica di cifratura, l'utente A del sistema RSA sceglie a caso due numeri primi piuttosto grandi p e q; il loro prodotto n = p ×q, unito ad un numero e, costituiscono la chiave pubblica PA = (e, n) del sistema. Il numero e è scelto in modo che gcd(e, f(n)) = 1 dove f(n) = (p - 1)(q - 1), è la funzione di Eulero. La chiave privata è costituita dalla coppia SA = (d, n), dove d è calcolato come l’inverso moltiplicativo di e mod f(n). La proprietà che e e f(n) sono primi garantisce sempre l'esistenza dell'inverso moltiplicativo d.

Cifratura e decifratura

Per effettuare la cifratura di un messaggio

M Î Zn,

il mittente A preleva dall'elenco la chiave pubblica PB dell'utente destinatario B e calcola il testo cifrato

C = PB (M) = Me mod n.

Il destinatario conoscendo la sua chiave segreta SB = (d, n) calcola il messaggio in chiaro

M = SB (C) = Cd mod n.

Correttezza

Verifichiamo ora che la fase di cifratura e quella di decifratura sono una l'inversa dell'altra. Poiché

ed º 1 mod f(n)

si ha

ed = t × f(n) + 1

con t intero e t ³1. Supposto che M Î Zn*, si ha:

Cd = Med = Med = Mt×f(n)+1 mod n = M

in quanto per il teorema di Eulero si ha che: xf(n) = 1 mod n.

Nel caso in cui la lunghezza di M sia maggiore di n, si avrebbe che M e (M mod n) originerebbero lo stesso crittogramma. Per ovviare a questo problema si assume che i messaggi siano numeri minori di n. Questo lo si può semplicemente ottenere decomponendo la sequenza di bit rappresentanti il messaggio in chiaro, in gruppi di l =ëlog2 nû bit ciascuno. Così facendo si garantisce che m < 2l < n. Questo è un semplice accorgimento cui tutti devono essere a conoscenza.

Nel casa in cui M Î Zn - Zn* per la correttezza si utilizza il teorema del resto cinese.

2.2 - Esempio RSA con piccoli numeri

Generazione delle chiavi

p = 47, q = 71

n = 47 × 71 = 3337, f(n) = 46 × 70 = 3220

·         A sceglie e tale che gcd(e,f(n)) = 1

e = 79

·         A calcola d = e-1 mod f(n)

d = 79-1 mod 3220 = 1019

·         La chiave pubblica è la coppia (e, n)

(e, n) = (79, 3337)

·         La chiave privata è la coppia (d, n)

(d, n) = (1019, 3337)

Cifratura

C = 68879 mod 3337 = 1570

Decifratura

·         A riceve il messaggio cifrato C = 1570

·         A si ricava M con la formula M = Cd mod n

M = 15701019 mod 3337 = 688

2.3 - Computazioni di RSA

Le procedure del crittosistema RSA si basano sull'elevazione a potenza modulare e sulla risoluzione di equazioni modulari.

2.3.1 - Elevazione a potenza modulare

L’operazione dell’elevazione a potenza modulare consiste nel calcolare xy mod z dove x, y e z sono interi. Presentiamo varie procedure per effettuare il calcolo.

Metodo naive

Intuitivamente si può semplicemente moltiplicare x per se stesso y volte facendo ad ogni passo modulo z per evitare cifre troppo grandi. Tale metodo è alla base del seguente algoritmo:

POTENZA MODULARE NAIVE(x,y,z)

    

a ¬ 1;

 

for i = 1 to y do

 

a¬ (a × x ) mod z

 

return a

 

 

 

 

Tale algoritmo in realtà non è utilizzato in quanto poco efficiente. Il numero cicli, infatti , è asintoticamente uguale a y. Quindi se y è di 512 bit si avranno 2512 cicli. I metodi realmente utilizzati sono due: il metodo "Left to right" e il metodo "Right to left".

Metodo Left-to-Right

Ricordando che vogliamo calcolare xy mod z, supponiamo che y0 y1y2y3…y t siano i bit da cui è formato y espresso in base due, il valore di y è quindi:

y = y0+2(y1+2(y2+2(y3…2(yt-1+2yt)…))) ,

da cui

.

Da tali considerazioni si ottiene il seguente algoritmo:

METODO LEFT TO RIGHT(x,y,z)

 

a ¬ 1;

 

for I = t downto 0 do

 

a¬ (a × a ) mod z

 

if yi = 1 then a¬ (a × x ) mod z

 

return a

 

 

 

Chiaramente tale algoritmo è migliore rispetto a quello precedente infatti se y è composto da 512 bit ora il numero di cicli è 512.

Metodo Right-to-Left

Anche tale metodo segue da considerazioni matematiche infatti si ha che:

y = y0 20 +y1 21 + ... + yt-1 2t-1 + yt 2t

da cui

Da ciò segue l’algoritmo per il calcolo di xy mod z :

METODO RIGHT TO LEFT(x,y,z)

   

if y = 0 then return 1

 

X ¬ x; P ¬ 1;

 

If y0 = 1 then X ¬ x

 

for I = 1 to t do

 

X ¬ (X × X) mod z

 

if yi = 1 then P ¬ (P × X ) mod z

 

return P

 

 

 

Anche questo metodo impiega 512 cicli se y è di 512 bit.

2.3.2 - Equazioni modulari

Le equazioni modulari consistono nel risolvere l’equazione ax º b (mod n). Tale calcolo richiede la conoscenza dell'algoritmo di Euclide e dell'algoritmo di Euclide Esteso.

Algoritmo di Euclide

L’algoritmo di Euclide, descritto negli "Elementi di Euclide" [300 A.C.], è utilizzato principalmente per il calcolo del Massimo Comune Divisore; l’algoritmo di Euclide esteso è utilizzato per la risoluzione delle equazioni lineari modulari. Il nostro interesse a risolvere tali equazioni dipende dal fatto che sono utilizzate per il calcolo di un parametro fondamentale nel sistema crittografico RSA. L’algoritmo di Euclide si basa sul "Teorema di ricorsione del Massimo Comune Divisore" che dice: "Per tutti gli interi a³ 0 e b>0 il gcd(a, b) è uguale al gcd(b, a mod b)".

EUCLIDE (a,b)

 

if b = 0 then return a

 

else return EUCLIDE (b, a mod b)

 

 

 

Assumendo a > b si ha che l’algoritmo di Euclide esegue al più log b chiamate, in ogni chiamata si hanno O((log a)2) operazioni sui bit da cui in totale si hanno O((log a)3) operazioni sui bit. Dall’analisi in realtà si ottiene che Euclide richiede al più O((log a)2) operazioni sui bit.

Esempio Consideriamo la computazione del gcd(30,21):

EUCLIDE(30,21) = EUCLIDE(21,9) = EUCLIDE(9,3) = EUCLIDE(3,0) = 3

In questa computazione ci sono solo tre chiamate ricorsive.

L’algoritmo non sarà ricorsivo all’infinito poiché il secondo parametro decresce strettamente in ogni chiamata ricorsiva. Così l’algoritmo di Euclide termina sempre con una risposta corretta.

Algoritmo di Euclide Esteso

La procedura prende in input due interi arbitrari (a e b) e restituisce una tripla (g, x, y) che soddisfa l’equazione:

g = gcd(a,b) = ax + by.

Il seguente pseudo-codice implementa l'algoritmo di Eulero Esteso:

EUCLIDE-ESTESO (a, b)

 

if b = 0 then return (a, 1, 0)

 

(g’, x’ ,y’) ¬ EUCLIDE-ESTESO (b, a mod b)

 

(g, x, y) ¬(g’, y’, x’ - ë a / b û y’)

 

return (g, x, y)

Quest’algoritmo permette di risolvere equazioni del tipo ax º b (mod n) o ax º1 (mod n). Tale algoritmo ha un tempo di esecuzione uguale all'algoritmo di Euclide.

Esempio EUCLIDE-ESTESO(99,78):

 

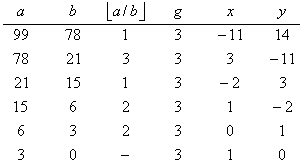
Da cui i valori finali: g = 3, x = -11 e y = 14.

Possiamo dimostrare che tali valori sono incorretti sostituendo tali valori in

g = gcd(a,b) = ax + by.

Quindi abbiamo che

3 = 99*-11 + 78*14

come volevasi dimostrare.

Risoluzioni di equazioni modulari

Supponiamo di voler risolvere l’equazione ax º b (mod n), tale equazione ha soluzione se e solo se g|b, dove g = gcd(a, n). In tal caso ci sono esattamente g distinte soluzioni modulo n:

x' (b/g) + i (n/g) per i = 0, 1, … g-1,

dove x’ si ottiene risolvendo l'equazione g = ax’ + ny utilizzando l’algoritmo EUCLIDE-ESTESO(a, n) precedentemente trattato.

Per ottenere le g distinte soluzioni si può usare il seguente algoritmo:

RISOLUZIONE-EQUAZIONI-LINEARI-MODULARI (a, b, n)

 

(g, x’, y’)¬ EUCLIDE-ESTESO(a, n)

 

if g|b

 

then x0 ¬ x’(b/g) mod n

 

for i = 0 to g- 1

 

do print (x0 + i (n/g))mod n

 

else print "nessuna soluzione"

 

 

 

 

Il tipo di equazioni lineari modulari utilizzate nell’RSA è ax º 1 (mod n), essa ha soluzione se e solo se gcd(a, n) = 1.

La soluzione è x’ dove 1 = ax’ + ny.

Usando EUCLIDE-ESTESO(a, n) è possibile ottenere tale soluzione, che viene denotata con a-1 mod n.

2.4 - Generazione di chiavi

L’algoritmo di generazione delle chiavi permette di generare la chiave pubblica (e,n) e la chiave privata (d,n). Tale algoritmo può essere schematizzato in 5 punti:

  1. Input L (lunghezza modulo)
  2. Genera 2 primi di lunghezza L/2
  3. n ¬ p × q
  4. scegli  1 < e < f(n), comunque piccolo
  5. if gcd(e, (p-1)(q-1)) = 1

then d ¬ e-1 mod (p – 1)(q – 1)

else goto 4

La lunghezza L definita nel punto 1 indica da quanti bit sarà composto n, è quindi fondamentale scegliere un valore appropriato per garantire una buona sicurezza. I due numeri generati al passo 2 sono di lunghezza L/2 perché il prodotto di tali numeri è di lunghezza L. Nei passi successivi (3,4,5) vengono generati e, d ed n; (e,n) rappresenta la chiave pubblica, (d,n) quella privata.

In realtà l’algoritmo utilizzato in pratica è il seguente:

  1. Input L (lunghezza modulo)
  2. e ¬ 3 oppure e ¬ 216 + 1
  3. Genera 2 primi di lunghezza L/2
  4. n ¬ p × q
  5. if gcd(e, (p - 1)(q - 1)) = 1

then d ¬ e-1 mod (p – 1)(q – 1)

else goto 3

La scelta di e = 3 oppure e = 216 + 1 = 65537 dipende dal fatto che la rappresentazione binaria che ne consegue contiene solo 2 bit uguali ad 1. Una simile rappresentazione facilita il processo di cifratura in quanto si possono usare i metodi, left-to-right o right-to-left, precedentemente descritti per effettuare l'elevazione a potenza modulare. Il fissare e in questo modo non fa perdere sicurezza al sistema, ma rende molto veloce il processo di cifratura. 

3 - Sicurezza di RSA

La sicurezza dell'RSA si basa sul fatto che la funzione di cifratura xe mod n è una funzione "one-way" che è computazionalmente difficile da invertire per un nemico che volesse decifrare un messaggio. Solo conoscendo la fattorizzazione di n è possibile trovare il valore delle chiavi. Infatti conoscendo la fattorizzazione di n è possibile calcolare f(n)=(p-1)(q-1) e calcolare d = e-1 mod f(n) usando l'algoritmo esteso di Euclide. Da ciò si deduce che la sicurezza dell'RSA dipende dal problema di fattorizzare grandi numeri. Di conseguenza il modo più ovvio di attaccare il sistema, è quello di tentare di risolvere quest’ultimo problema. Gli algoritmi più efficienti, conosciuti fino ad ora, hanno una complessità

.

Fattorizzare un numero di 664 bit richiede almeno 1023 passi usando gli algoritmi più efficienti; per cui ipotizzando di avere una rete costituita da un milione di computer con ciascuno di loro che esegue un milione di passi al secondo, il tempo impiegato per fattorizzare n sarebbe dell'ordine dei 4000 anni. Se poi n fosse un numero a 1024 bit la stessa rete impiegherebbe 1010 anni per fattorizzarlo . Ciò sottolinea l’osservazione fatta nell’introduzione e cioè che non è impossibile decifrare un testo cifrato con il crittosistema RSA, ma piuttosto è computazionalmente difficile.

3.1 - Fattorizzazione

Fattorizzare un numero n significa trovare i suoi fattori primi. Il problema della fattorizzazione è uno dei più vecchi nella teoria dei numeri. In questa sezione faremo una discussione informale sui migliori algoritmi di fattorizzazione conosciuti. Attualmente, gli algoritmi capaci di fattorizzare in modo efficiente numeri molto grandi, sono due:

• Quadratic Sieve. Questo è l'algoritmo più veloce conosciuto per numeri con meno di 150 cifre decimali; mentre per un numero maggiore di cifre è chiamata Multiple Polynomial Quadratic Sieve. Per questo algoritmo la versione più veloce è Double Large Prime Variation of the Multiple Polynomial Quadratic Sieve.

• Number Field Sieve (NFS) . Questo è l'algoritmo di fattorizzazione conosciuto più veloce. Quando fu proposto non era molto pratico, ma c' è stato un cambiamento dovuto alle implementazioni degli ultimi anni. L' algoritmo Multiple Polynomial Quadratic Sieve è più veloce per numeri piccoli (da 110 a 135 cifre decimali a secondo delle implementazioni).

Esistono altri algoritmi di fattorizzazione che però sono stati sostituiti da questi due menzionati sopra:

• Elliptic Curve Method (ECM) . Questo metodo è stato molto usato per trovare fattori di numeri a 38 cifre, ma non più grandi. Per numeri più grandi, gli altri algoritmi sono più veloci.

• Trial Division. Questo è il più vecchio algoritmo di fattorizzazione, ed implica il controllo di ogni numero primo minore o uguale della radice quadrata del numero candidato. Se n < 1012, questo è un metodo di fattorizzazione ragionevole, ma per n più grande abbiamo tecniche più sofisticate.

.3.1.1 - Quadratic Sieve

Questo algoritmo fu inventato da Pomerance agli inizi degli anni ‘80.E basato su un’idea molto semplice: se riusciamo a trovare x e y tali che x2 º y2 mod n e x ¹ ± y mod n allora gcd(x – y, n) è un fattore non banale di n.Il metodo usa una factor base, che è un insieme B di primi piccoli. Ricaviamo diversi interi x tali che tutti i fattori primi di x2 mod n stiano nella factor base B. (Come questo sia fatto lo vedremo dopo). L’idea è di prendere il prodotto di diversi x in modo che ogni primo nella factor base venga usato un numero pari di volte. Così avremo una congruenza del tipo desiderato x2 º y2 mod n, che può portarci ad una fattorizzazione di n.

Esempio Consideriamo n = 15770708441. Sia B = {2; 3; 5; 7; 11; 13} la factor base. Consideriamo le tre congruenze:

(8340934156)² º 3 × 7 mod n

(12044942944)² º 2 × 7 × 13 mod n

(2773700011)² º 2 × 3 × 13 mod n

Se prendiamo il prodotto di queste tre congruenze, abbiamo:

(8340934156 × 12044942944 × 2773700011)² º (2 × 3 × 7 × 13) ² mod n

Riducendo l'espressione nella parentesi modulo n, abbiamo

(9503435785)² º (546)² mod n

Quindi calcolando gcd(9503435785-546; 15770708441); troviamo il fattore 115759 di n.

Supponiamo che B={p1, p2, ... pB} sia la factor base. Sia C leggermente più grande di B (diciamo C = B + 10) e supponiamo di aver ottenuto C congruenze:

xj2 º p1a1j × p2a2j × ... × pBaBj mod n per 1 £ j £ C

Per ogni j, consideriamo il vettore:

aj = {a1j mod 2, ..., aBj mod 2}Î (Z2)B

Se riuscissimo a trovare un sottoinsieme degli aj che sommati modulo 2 danno il vettore (0,0,…… ), allora il prodotto dei corrispondenti xj userà ogni fattore di B un numero pari di volte. Vediamo con un esempio che esiste una dipendenza anche se C < B.

Esempio I tre vettori a1; a2; a3 sono:

a1= (0; 1; 0; 1; 0; 0)

a2= (1; 0; 0; 1; 0; 1)

a3= (1; 1; 0; 0; 0; 1)

E’ facile vedere che

a1 + a2 + a3 = (0,0,0,0,0,0) mod 2

Questo dà origine alla congruenza che abbiamo visto nell'esempio 1 che fattorizza n. Osserviamo che per trovare un sottoinsieme di C vettori a1, ..., aC, la cui somma modulo 2 è il vettore di tutti zeri, non è niente di più che trovare una combinazione lineare (su Z2) di questi vettori. Dato C > B, tale dipendenza lineare deve esistere e può essere trovata facilmente usando il metodo standard dell’eliminazione gaussiana. La ragione del perché C > B + 1 è che non c' è nessuna garanzia che una data congruenza x² º y² mod n produrrà la fattorizzazione di n. Approssimativamente solo per il 50% delle volte accade che x º ± y mod n mod n. Ma se C > B + 1, allora possiamo ottenere varie di queste congruenze (che sorgono da dipendenze lineari diverse tra gli aj ).

Resta da discutere come otteniamo gli interi xj tali che xj2 mod n fattorizzino completamente sulla factor base B. Un metodo usato comunemente è usare gli interi della forma:

xi = i + ë n1/2û i=1,2,...

Allora una procedura al setaccio è usata per determinare quegli xi che sono fattori su B. C' è naturalmente un trade­off : se B = |B| è grande, allora abbiamo bisogno di più congruenze prima di poter trovare una relazione di dipendenza.

3.1.2 - Algoritmi in pratica

Nel caso peggiore, il running time asintotico degli algoritmi quadratic sieve e elliptic curve è essenzialmente lo stesso. Ma in tale situazione, quadratic sieve supera elliptic curve poichè le costanti nascoste sono più piccole. Il metodo elliptic curve è più utile se i fattori primi di n sono di taglia diversa. Un numero molto grande che fu fattorizzato usando il metodo dell'elliptic curve fu il numero di Fermat 2211-1 nel 1988 da Brent. Per fattorizzare i moduli dell’RSA (dove n = pq; p e q sono primi e sono circa della stessa lunghezza) il quadratic sieve è ora l’algoritmo che ha più successo. Nel 1983, il quadratic seive fattorizzò con successo un numero di 69 cifre che era un fattore (composto) di 2251( questo calcolo fu fatto da David, Holdredge e Simmons).Con il progresso i numeri sono saliti fino a 106 cifre furono fattorizzati con questo metodo da Lenstra e Manasse, che distribuirono i calcoli a centinaia di postazioni di lavoro separate (chiamarono questo approccio "fattorizzazione tramite posta elettronica"). La fattorizzazione di un RSA­120 (che è una lista di numeri composti che sono dell'ordine di 120 cifre) richiese 825 MIPS­anni (MIPS= un milione di istruzioni per secondo) di tempo di computazione e si usò una factor base di cardinalità 245810. Il Number Field Sieve è il più recente dei tre algoritmi, e sembra avere una grande potenzialità poiché il suo runnig time asintotico è più veloce sia del Quadratic sieve sia dell’Elliptic curve. E’ ancora in fase di sviluppo, ma si pensa che il Number field sieve potrebbe provare di essere più veloce per numeri che hanno più di 125­130 cifre.

Carl Pomerance ha progettato una macchina di fattorizzazione modulare. La grandezza del numero che si può fattorizzare dipende da quanto è grande la macchina che si può fornire. Il modello di dimostrazione di Pomerance è un’implementazione di $ 25.000 che può fattorizzare numeri di 100 cifre in due settimane. Una macchina di $ 10 milioni potrebbe fattorizzare un numero di 150 cifre in un anno. Teoricamente non ci sono limiti per questo modello di fattorizzazione. Per fattorizzare un numero di 200 cifre in un anno, la macchina costerebbe $ 100 bilioni.

3.2 - Attacchi RSA

Osserviamo che per un crittoanalista rompere l'RSA equivale a calcolare f(n). Infatti, se n e f(n) sono conosciuti ed n è il prodotto di due primi p e q, n può essere facilmente fattorizzato risolvendo le due seguenti equazioni: n = p × q e f(n)= (p - 1)(q - 1). Nelle due incognite p e q. Sostituendo q = n / p nella seconda equazione se ne ottiene un’unica di secondo grado nella sola incognita p:

p2 - (n - f(n) + 1)p + n = 0.

Le due radici di questa equazione sono i fattori p e q. Quindi se un crittoanalista conosce il valore di f(n) può fattorizzare n e rompere il sistema.

Esempio Supponiamo che il crittoanalista conosca f(n) = 84754668 e n = 84773093.Queste informazioni gli permettono di scrivere l'equazione: p2 - 18426p + 84773093 = 0. Risolvendo l’equazione si ottengono le due radici 9539 e 8887 che rappresentano i fattori p e q di n.

3.2.1 - Attacco Chosen Ciphertext

Mostriamo questo tipo di attacco nei seguenti casi:

CASO 1: consideriamo due utenti di una rete, Oscar e Alice, e supponiamo che Oscar intercetti le comunicazioni di Alice prelevando i messaggi cifrati C. Matematicamente Oscar vuol calcolare M = Cd. Per calcolare M egli sceglie per primo un numero casuale r tale che r < n, ed inoltre conosce la chiave pubblica e di Alice. Egli può calcolare:

x = re mod n

y = xC mod n

t = r-1 mod n

Se x = re mod n allora r = xd mod n per cui t = x-d mod n.Ora Oscar manda y ad Alice chiedendone la firma, e Alice spedisce ad Oscar u = yd mod n (da notare che Alice ha firmato y e non una sua versione hash). Oscar può calcolare:

tu mod n = x-d yd mod n = x-d xd Cd mod n = Cd mod n = M

CASO 2: supponiamo di avere un computer Hall che notifichi documenti. In altre parole se un utente vuole farsi notificare un documento, lo spedisce ad Hall, il quale lo firma con la sua chiave privata, e lo rispedisce al mittente. (Non sono utilizzate funzioni one-way hash). Supponiamo che Oscar voglia farsi notificare un documento N da Hall il quale per una ragione qualsiasi non voglia farlo. Per prima cosa Oscar sceglie un valore arbitrario X e calcola Y = Xe, prelevando la chiave pubblica e di Hall. In seguito calcola M = Y N e fa firmare M da Hall. Quindi Hall gli ritorna Md mod n, da ciò Oscar calcola

(Md mod n) X-1 = Nd mod n

cioè la firma del documento N. Questo è possibile perché l'esponenziazione preserva la struttura moltiplicativa dell'input, cioè:

(XM)d = Xd Md mod n

CASO 3: Oscar vuole far firmare a Bob un documento M3 che Bob non vuole firmare. Allora Oscar, genera due documenti M1, M2 tali che:

M3 º M1 M2 mod n

Quindi manda alla firma di Bob sia M1 che M2 e calcola:

M3d mod n = M1d mod n M2d mod n

che è la firma di M3.

3.2.2 - Attacco Common Modulus

Supponiamo che due utenti usano un modulo comune n ed esponenti di crittazione e1ed e2 con gcd(e1, e2) = 1. Se viene inviato lo stesso messaggio M ad entrambi, allora vengono calcolati i testi cifrati come:

C1 = Me1 mod n

C2 = Me2 mod n

Se entrambi C1, C2 vengono intercettati allora un intruso può, usando l'algoritmo di Euclide, calcolare r ed s tali che :

re1 + se2 = 1

e quindi ottenere

M = C1r C2s mod n.

3.2.3 - Attacco Low Exponent

A priori l'esponente di crittazione e nello schema RSA è arbitrario. Comunque, si consiglia di scegliere un valore di e in modo da essere lo stesso per tutti gli utenti del sistema. Scegliere e = 2 è impossibile in quanto 2 non è primo con p - 1 o q - 1. Ci sono comunque interessi teorici nella scelta del valore 2 in quanto Rabin e Williams hanno notato che modificando l’RSA ed usando 2 come esponente, un attacco del tipo ciphertext-only è tanto difficile quanto fattorizzare.

La scelta del valore 3 può essere fatta nell'RSA; essa comporta vantaggi dovuti alla semplicità della codifica e decodifica dei messaggi. Questo valore ed altri esponenti dello stesso ordine di grandezza sono consigliati anche se comunque soffrono di qualche problema. Illustriamo cosa comporta la scelta del valore e = 3. Per prima cosa gli utenti devono essere sicuri che ogni blocco M che deve essere codificato soddisfi la relazione M³ >> n. E’ consigliabile rispettare tale relazione perché essendo C = M³ mod n diviene semplicemente C = M³ se M³ < n. In questo caso la ricerca di M si riduce al semplice problema del calcolare una radice cubica. Così l'uso di e = 3 fa si che essa possa essere scelta in un sottoinsieme di [0; n) piuttosto che l'intero intervallo come sarebbe preferibile. Ci possono essere altri problemi nello scegliere e = 3. Infatti supponiamo che A mandi lo stesso messaggio ad ognuno dei Bi, con i = 1, 2, 3. Supponiamo che i vari Bi usino come modulo ni e M < ni per ogni i. Assumiamo che ognuno degli {n1, n2, n3} siano generati come prodotto di due numeri primi casuali; la probabilità fra i sei primi usati è circa zero. Dunque può essere soddisfacente assumere che gli ni siano coppie relativamente prime.

Sia Ci = M³ mod ni. Supponiamo che i tre messaggi cifrati siano intercettati. Usando il teorema Cinese del resto, il nemico può trovare x nell' intervallo [0; n' ), con n' = n1n2n3 dove x º Ci mod ni con i = 1 ,2, 3. Quindi x ºM mod n'. Essendo M³ < n' risulta M³ = x, così M = x1/3. Quindi il testo in chiaro M può essere facilmente recuperato dai tre testi cifrati. Concludendo, l'uso di e = 3 o di altri esponenti dello stesso ordine di grandezza, rendono l'RSA vulnerabile rispetto ad attacchi di tipo ciphertext-only. Il mittente può cercare di modificare M per ogni destinatario in modo da evitare questo attacco. Hastad ha dimostrato che in generale la scelta di un basso esponente rende comunque l'RSA vulnerabile se ci sono dipendenze lineari tra parti del testo in chiaro.

4 - Bibliografia