2. Modello di crittografia visuale per immagini in bianco e nero

In questo capitolo vengono riveduti i concetti principali visti nella precedente sezione utilizzando un maggior formalismo.
Esaurita questa prima parte, si passa alla descrizione di un modello di VCS per strutture a soglia e quindi ad un modello di VCS per strutture di accesso generali.

2.1 Concetti principali

Come detto in precedenza, si assume che l'immagine originale sia strutturata come una collezione di pixel bianchi e neri. In fase di codifica ogni pixel viene trattato separatamente dagli altri; a ciascuna delle n share viene assegnata dal dealer una versione codificata del pixel, che consiste di m sottopixel. La sovrapposizione delle n share permette il recupero del pixel originario. Si ricordi che, nella fase di sovrapposizione dei lucidi, i sottopixel bianchi vengono trattati come trasparenti.

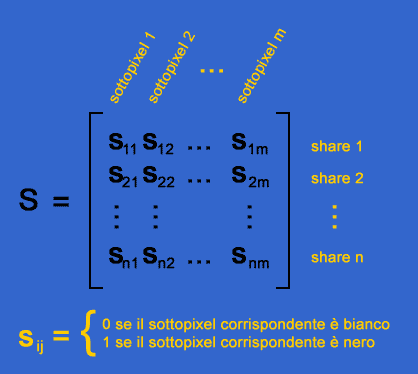
Per rappresentare la codifica di un pixel dell'immagine originale si fa uso di una matrice booleana S di dimensioni n x m, in cui l'elemento di posizione (i,j) indica il colore del j-esimo sottopixel nella i-esima share (e quindi relativa all'i-esimo partecipante): il valore booleano '1' indica il colore nero, il valore '0' indica il colore bianco. La Figura 8 mostra una generica matrice S e la Figura 9 un semplice esempio.

Figura 8 - Matrice n x m con indicazione delle righe e delle colonne

Figura 9 - Matrici S0 e S1 relative allo schema a soglia (2,2) con m=2, visto nel paragrafo 1.1

La sovrapposizione delle share di r partecipanti (con rn) equivale all'OR booleano delle r corrispondenti righe di S. Il pixel risultante dalla sovrapposizione delle share viene rappresentato come un vettore V di m valori, uno per ciasciun sottopixel. Il numero di '1' presenti nel vettore V è detto peso di Hamming, e si indica con H(V).

Indicando con il parametro d (1 d m) il numero di sottopixel neri utilizzati per rappresentare un pixel nero, nella formalizzazione del modello risulta che:

• per ogni vettore V, se H(V) d, il sistema visivo umano riconosce come nero il pixel rappresentato da V;
• per ogni vettore V, se H(V) < d - ·m, il pixel sarà visto come bianco.

Ciò evidenzia che l'efficacia di uno schema di crittografia visuale in bianco e nero dipende fortemente dal parametro d e dalla differenza relativa .

Si osservi che non è possibile codificare un pixel bianco (rispettivamente un pixel nero) con m sottopixel bianchi (rispettivamente neri), altrimenti uno dei partecipanti avrebbe l'informazione completa sul colore del pixel.

2.2 VCS per strutture a soglia

Uno schema a soglia (k,n) consiste di due collezioni di matrici C0 e C1, di dimensione n x m. Gli insiemi C0 e C1 contengono tutte le possibili matrici che codificano, rispettivamente, un pixel bianco e un pixel nero, in uno schema ad n partecipanti ed espansione m. Per condividere un pixel bianco del segreto, il dealer sceglie casualmente una delle matrici in C0, mentre per condividere un pixel nero sceglie casualmente una delle matrici in C1. La matrice scelta per condividere il pixel definisce il colore degli m sottopixel in ciascuna delle n share.
Si noti che, scegliendo arbitrariamente una matrice S0 in C0 (rispettivamente una matrice S1 in C1), è possibile generare tutte le matrici in C0 (risp. in C1) mediante permutazioni delle colonne di S0 (risp. S1). Per questo motivo, S0 ed S1 vengono dette matrici di base.

La soluzione è considerata valida se si ha che:

1. per ogni matrice S in C0, il vettore V risultante dall'OR di un qualsiasi insieme di k righe soddisfa la relazione H(V) < d - ·m (il pixel appare bianco);
2. per ogni matrice S in C1, il vettore V risultante dall'OR di un qualsiasi insieme di k righe soddisfa la relazione H(V) d (il pixel appare nero);
3. Considerato un insieme Q={i1, i2, ..., iq}, con q<k ed i cui elementi indicano q partecipanti, si definiscano D0 e D1 come le collezioni di matrici, di dimensioni q x m, ottenute, rispettivamente, dalla restrizione delle matrici in C0 e C1 alle q righe referenziate da Q. Scelta una matrice in (D0 U D1), non si ha alcuna informazione addizionale per stabilire se proviene da D0 o D1.

Si osservi che le condizioni 1 e 2 assicurano che tra un pixel bianco e un pixel nero, nell'immagine ricostruita dalla sovrapposizione delle share, vi sia una differenza di contrasto pari almeno ad ; la condizione 3, invece, indica che impiegando meno di k share non si riesce a stabilire se un pixel dell'immagine originale è bianco o nero.

2.2.1 Schema a soglia (2,n)

Lo schema a soglia (2,n) può essere realizzato direttamente costruendo gli insiemi C0 e C1 nel seguente modo:

C0 = tutte le possibili permutazioni delle colonne della matrice n x n S0=       C1 = tutte le possibili permutazioni delle colonne della matrice n x n S1 =

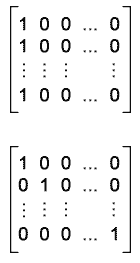Calcolando l'OR di due righe di una matrice in C0, si ottiene un vettore con un unico elemento uguale ad '1' ed n-1 elementi uguali a '0'. Calcolando, invece, l'OR di due righe di una matrice in C1, si ottiene un vettore con 2 elementi uguali ad '1' ed n-2 elementi uguali a '0'.

Tale differenza ci dà la possibilità di distinguere un pixel bianco da un pixel nero. Considerando, però, una singola riga, questa sarà composta da un unico '1' ed n-1 '0', indipendentemente dal fatto che provenga da una matrice in C0 o da una matrice in C1.

I parametri di questo schema assumono i seguenti valori:

• d= 2
• m= n
• = 2/m - 1/m = 1/m = 1/n

2.2.2 Schema a soglia (3,n)

La costruzione di uno schema a soglia (3,n) avviene nel seguente modo:

sia B una matrice di dimensione n x (n-2) formata da tutti '1' e sia I la matrice identità di dimensione n x n; si generi la matrice BI, di dimensione n x (2n-2), ottenuta dalla concatenazione di B ed I. C0 e C1 verranno costruite come segue:

C0 = tutte le matrici ottenute permutando le colonne di S0=c(BI), complemento bit a bit di BI;
C1 = tutte le matrici ottenute permutando le colonne di S1=BI.

Le matrici appartenenti a C0 e C1 godono delle seguenti proprietà (si faccia riferimento all'esempio di uno schema a soglia (3,4) in Figura 10):

• ogni singola riga contiene n-1 sottopixel neri ed n-1 sottopixel bianchi;
• ogni coppia di righe ha n-2 sottopixel neri nelle stesse posizioni e 2 sottopixel neri in posizioni diverse;
• l'OR su una qualsiasi tripla di righe prese da una matrice in C0, è caratterizzato da n sottopixel neri;
• l'OR su una qualsiasi tripla di righe di una matrice in C1, è caratterizzato da (n+1) sottopixel neri.

Figura 10 - Esempio di costruzione di uno schema a soglia (3,4)

Nell'esempio dello schema a soglia (3,4), visto in Figura 10, i parametri assumono i seguenti valori:

• d= 5
• m= 6
• = 5/6 - 4/6 = 1/6

2.2.3 Soluzione ottimale per uno schema a soglia (n,n)

Si consideri l'insieme W={1,2,...,n} con il relativo insieme 2^w, formato da tutti i 2ⁿ possibili sottoinsiemi di W, e si indichino con e , rispettivamente, la lista formata dagli elementi di 2^wdi cardinalità pari e la lista formata dagli elementi di 2^w di cardinalità dispari (si faccia riferimento alla Figura 11 per un esempio).

Posto m=||=||= 2^n-1, si costruiscono le matrici S0 e S1, di dimensione n x m, nel seguente modo:

S0[i,j]=1 se e solo se i j, dove con j si intende il j-esimo elemento di ;
S1[i,j]=1 se e solo se i j, dove con j si intende il j-esimo elemento di .

Figura 11 - Esempio di costruzione di uno schema a soglia (3,3)

Come visto precedentemente, gli insiemi C0 e C1 sono ottenuti, rispettivamente, da tutte le possibili permutazioni delle colonne di S0 ed S1.

Si noti che le colonne della matrice S0 (risp. S1) sono tutti i possibili vettori di lunghezza n con un numero pari (risp. dispari) di '1' .

Questo procedimento dà luogo ad uno schema caratterizzato da un contrasto =½^n-1. Tale soluzione è ottimale poiché vale il seguente teorema (dimostrato da Naor e Shamir) :

TEOREMA. In ogni schema a soglia (n,n) si ha ½^n-1 e m2^n-1

2.3 VCS per strutture di accesso generali

Finora si sono esaminati schemi a soglia (k,n), dove il segreto poteva essere ricostruito da qualsiasi sottoinsieme dei partecipanti di cardinalità almeno k.
Talvolta si richiede che il segreto possa essere ricostruito solo da alcuni specifici sottoinsiemi dell'insieme dei partecipanti, detti autorizzati (qualified); i sottoinsiemi non abilitati alla ricostruzione del segreto si dicono proibiti (forbidden). La coppia (sottoinsiemi autorizzati, sottoinsiemi proibiti) determina una struttura di accesso.
Lo schema a soglia (k, n), visto nel paragrafo precedente, è una particolare struttura di accesso dove i sottoinsiemi autorizzati sono tutti quelli che hanno cardinalità almeno k.

Si consideri l'insieme dei partecipanti P={p1,p2,...,pn} con il relativo insieme 2^p, formato da tutti i possibili sottoinsiemi di P.
Si denoti con Q 2^p, la famiglia dei sottoinsiemi di partecipanti qualificati a ricostruire il segreto, e con F 2^p, la famiglia dei sottoinsiemi di partecipanti NON qualificati a ricostruire il segreto. Naturalmente, QF = , ma (Q,F) non è necessariamente partizione di 2^p.
La coppia (Q,F) è detta struttura di accesso dello schema.

Un partecipante p è detto essenziale se esiste un sottoinsieme di P che non può ricostruire il segreto senza la share di p. Formalmente, p è essenziale se X F | X {p} Q.

Si assumerà che tutti i partecipanti siano essenziali, in quanto un partecipante non essenziale possiede un'informazione non necessaria ad alcun sottoinsieme di P per recuperare l'immagine condivisa.

Q è detto monotono crescente, se aggiungendo un partecipante ad un sottoinsieme qualificato, questo continua ad essere qualificato. Formalmente, Q è monotono crescente se X Q e p P-X si ha che X {p} Q.

F è detto monotono decrescente, se sottraendo un partecipante ad un insieme non qualificato, questo continua ad essere non qualificato.
Formalmente, F è monotono decrescente se X F e X' X si ha che X' F.

Una struttura di accesso (Q, F) è detta forte se Q è monotono crescente e F è monotono decrescente.

L'insieme Q0 = { A Q | A' A, A' Q} è la famiglia minimale di tutti i sottoinsiemi qualificati. In altre parole, Q0 è costituito da quei sottoinsiemi qualificati tali che ogni partecipante è indispensabile, nell'ambito del sottoinsieme di appartenenza, per la ricostruzione del segreto.

Se (Q, F) è una struttura forte, Q0 si dice base e Q è chiusura di Q0, cioè : Q = { C P| B C: B Q0}.
In altri termini, ogni insieme in Q è ottenuto aggiungendo ad un insieme di Q0, un sottoinsieme di P.

La coppia (Q,F) è considerata struttura di accesso valida se si ha che:

1. ogni insieme qualificato X = {i1, i2, ..., ip} Q può recuperare l'immagine condivisa sovrapponendo le share dei partecipanti appartenenti all'insieme. Formalmente, per ogni S C0, il vettore V, corrispondente all'OR delle righe i1, i2,..., ip di S, soddisfa la relazione H(V) d - ·m, mentre per ogni S C1 risulta H(V)d;
2. ogni insieme non qualificato Y={i1, i2, ..., iq} non ha nessuna informazione sull'immagine considivisa. Formalmente, si definiscano D0 e D1 come le collezioni di matrici, di dimensioni q x m, ottenute, rispettivamente, dalla restrizione delle matrici in C0 e C1 alle q righe referenziate da Y. Scelta una matrice in (D0 U D1), non si ha alcuna informazione addizionale per stabilire se proviene da D0 o D1.

Segue un esempio di un VCS per strutture di accesso.

Esempio. Si supponga n=4 e P={1,2,3,4}. Si definiscano:

Q= { {1,2}, {2,3}, {3,4}, {1,2,3} }
F= { {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4} }

Si ricava che:

Q0= { {1,2}, {2,3}, {3,4} }

Si osservi che la struttura di accesso (Q,F) definita NON è una struttura forte (in quanto, ad esempio, {1,2} è qualificato mentre {1,2,4} non lo è).

Le matrici di base S0 ed S1 sono:

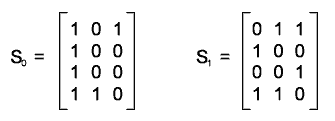
Come si evince dalle matrici di base, m=3 e =1/3.

Nella seguente tabella sono riportati gli insiemi qualificati e non con i relativi pesi di Hamming.

La tabella mostra che, per ogni insieme qualificato, H(V) varia a seconda che V sia ricavato da S0 o da S1; tale valore, invece, non cambia per gli insiemi non qualificati. Sugli insiemi restanti il comportamento non è definito.