4.1 Luce e colori

La luce può essere considerata come formata da un flusso di fotoni, ognuno dei quali è caratterizzato da una specifica energia detta frequenza del fotone; tale energia corrisponde al colore riconosciuto quando il fotone stesso colpisce l'occhio umano. L'intensità di un fascio di luce dipende dal numero dei fotoni che lo compongono.

Lo spettro visibile, cioè l'arco delle radiazioni elettromagnetiche cui l'occhio umano è sensibile, è formato da luci monocromatiche  che, sovrapposte, danno la luce bianca: cioè, la luce bianca è un flusso di fotoni di tutte le possibili frequenze visibili (tutti i colori).

Il primo a dimostrare che un raggio di luce bianca, qual è quella del sole, risulta composta da tante radiazioni di colore diverso, è stato, nel 1666, Isaac Newton. Infatti egli scoprì che quando un ristretto fascio di luce, proveniente dalla fessura di una finestra chiusa, viene fatto incidere su un prisma triangolare di vetro, da questo fuoriescono, con inclinazioni diverse, tanti fascetti di vari colori, nell'ordine: rosso, arancio, giallo, verde, blu e violetto, ossia i colori dell'iride.

In realtà, sebbene il numero dei colori dispersi sia incalcolabile, in quanto possiamo suddividere ogni intervallo di lunghezza d'onda in ulteriori intervalli comunque piccoli, la sensazione visiva per l'occhio è riducibile a sei famiglie di colori principali. Facendo ripassare tutti i fascetti colorati attraverso un secondo prisma uguale al primo, ma capovolto, Newton riuscì anche a ripristinare il fascio di luce bianca, offrendo così la controprova che la luce bianca può essere considerata come una mescolanza di tante radiazioni monocromatiche.

Successivamente alcuni ricercatori, sviluppando le osservazioni di Newton, giunsero a stabilire che sono sufficienti tre radiazioni monocromatiche per ottenere sia la luce bianca, sia tutte le altre luci colorate. Fu il fisico e fisiologo tedesco Hermann Helmholtz che, sul finire del 1800, perfezionò tale teoria, già formulata in modo embrionale dal medico-scienziato inglese Thomas Young intorno al 1860.
Questa teoria, detta tricromatica, prende per l'appunto avvio dal fatto che, volendo riottenere la luce bianca dopo la scomposizione con un prisma, non è necessario rimiscelare tutte le radiazioni ottenute, ma è sufficiente impiegare tre radiazioni tratte da zone dello spettro abbastanza distanti fra loro.
Inoltre, dosando opportunamente le intensità delle tre radiazioni, si possono ricavare le sensazioni visive di tutti gli altri colori dello spettro.

Le terne di radiazioni con cui è possibile avere questi risultati sono varie, pertanto non è facile stabilire quali siano le lunghezze d'onda genuinamente fondamentali o primarie.
Tuttavia i migliori risultati si hanno con tre bande di frequenza che, quando agiscono separatamente, danno luogo alla visione di un certo tipo di rosso vivo, di un certo tipo di verde e di un certo tipo di blu, tendente al violetto, e che sono tratte, rispettivamente, dalle regioni di onde lunghe, medie e corte dello spettro visibile.
Pertanto oggi i fisici considerano convenzionalmente come colori primari il rosso, il verde e il blu.

Esistono due tipologie di mescolanze cromatiche: la prima riguarda l'addizione di luci colorate (sintesi additiva); la seconda, la combinazione di materie coloranti (sintesi sottrattiva).

La sintesi additiva

Supponiamo di disporre di tre fasci luminosi: uno rosso, uno verde e uno blu, di giusta lunghezza d'onda e d'intensità appropriata.
Proiettando in un ambiente buio, sopra uno schermo bianco, il fascio di luce rossa, otterremo ovviamente un cerchio dello stesso colore.
Proiettando sul medesimo schermo il fascio di luce verde, nel punto in cui rosso e verde si sovrappongono appare un nuovo colore: il giallo.
Proiettando il rimanente fascio di luce blu avremo che dove blu e verde si sovrappongno appare un colore azzurro turchese che è chiamato cyan (o ciano).
Nella zona in cui sono il blu e il rosso a sovrapporsi, invece, appare un caratteristico colore rosso purpureo che è chiamato magenta.
Infine, nella zona in cui convergono tutte e tre le luci colorate, lo schermo diffonde una luce che all'occhio appare bianca alla pari di quella del sole.

L'operazione fin qui descritta viene detta sintesi additiva proprio perché, a partire dall'assenza di luce (l'ambiente oscurato), giunge per progressiva somma di luci a produrre la sensazione del bianco.

Le tre luci-colore in questione (rossa, verde, blu) si chiamano primarie, mentre le altre, conseguite per mezzo di miscelamenti, si chiamano secondarie o derivate.
Variando opportunamente l'intensità dell'una o dell'altra delle tre luci, si avranno ulteriori apparizioni di colori secondari più o meno saturi.

Resta da osservare che non è solo la terna di luci monocromatiche a dare luce bianca in quanto anche la somma di una luce primaria con quella ottenuta dalla mistura delle altre due luci primarie produce lo stesso risultato.
Nella sintesi additiva, si parla di coppie di colori complementari ogni volta che due luci colorate, mescolandosi, producono lo stesso risultato della somme delle tre luci primarie, ossia il bianco. Tali coppie risultano ovviamente costituite da un colore primario e da uno risultante dalla mistura degli altri due primari, per cui sono comunque compresenti il rosso, il verde e il blu.

In particolare: il giallo è complementare del blu (e viceversa), il cyan è complementare del rosso, il magenta è complementare del verde.

La sintesi sottrattiva

E' il genere di procedimento che viene messo in atto nella comune esperienza di mescolare assieme sostanze coloranti di vario tipo (vernici, oppure inchiostri, acquarelli, etc.), o anche di sovrapporre fra loro vetri o fogli di cellophan colorati. In tutti questi casi si verifica una situazione che è all'opposto di quella precedente: non vi è infatti somma di due o più radiazioni luminose, ma vi è invece sottrazione.

Quando l'occhio umano associa uno specifico colore alla superficie di un oggetto (detta anche filtro), significa che quest'ultima assorbe tutte le frequenze di fotoni, tranne quelle che determinano il colore riconosciuto; quindi, quando si guarda il filtro, il colore che si vede è quello riflesso (o meglio non assorbito) dalla superficie.

Si consideri, ad esempio, un foglio di carta come un mezzo che riflette la luce. Se il foglio appare bianco, vuol dire che riflette tutte le radiazioni contenute nella luce.
Appoggiando sul foglio un lucido giallo, delle tre radiazioni principali presenti nello spettro, quella blu viene assorbita e le altre due (la rossa e la verde) vengono invece riflesse, cosicché il foglio appare, per l'appunto, giallo. Utilizzando altri lucidi, rispettivamente di colore magenta e cyan, si otterranno risultati analoghi.

Si prosegua nell'esperimento appoggiando sul foglio un lucido giallo ed uno cyan, sovrapponendoli.
Il giallo sottrae la radiazione blu e il cyan la radiazione rossa. L'unica radiazione riflessa è quella verde, per cui il foglio apparirà di tale colore.
In maniera analoga si ottiene il rosso, sovrapponendo il giallo e il magenta, e il blu, sovrapponendo il magenta e il cyan.
Se si sovrappongono tutti e tre i lucidi giallo, magenta e cyan, tutte le radiazioni vengono assorbite e come risultato si avrà un colore brunastro, tanto più tendente al nero quanto più i lucidi impiegati saranno al massimo della loro saturazione cromatica.

Se, dunque, nella sintesi additiva si parte dall'assenza di luce, ossia dal nero, per giungere alla somma di tutte le radiazioni cromatiche nel bianco, viceversa nella sintesi sottrattiva si parte dalla luce, ossia dal bianco, e per sottrazioni successive si giunge all'assenza di radiazioni visibili, cioè al nero.

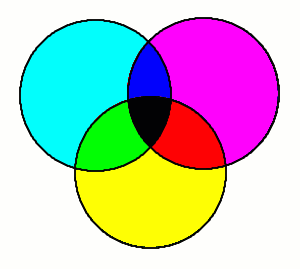
Figura 16 - Sintesi sottrattiva

La sovrapposizione sfalsata di tre superfici trattate con sostanze coloranti trasparenti la cui tinta è giallo, magenta e cyan (nel nostro caso si tratta degli inchiostri da stampa per produrre le trasparenze o lucidi) dà luogo, nelle zone di sovrappposizione, a un colore rosso vivo (giallo e magenta), a un colore verde (giallo e cyan), a un colore blu violaceo (magenta e cyan) e infine a una specie di nero (giallo, magenta e cyan).

Dunque, nella sintesi sottrattiva, giallo , magenta e cyan sono i colori primari cioè sono i colori che non possiamo ottenere per mescolanza. Rosso, verde e blu sono invece colori secondari.

Confrontando lo schema di Figura 16 con quello di Figura 15, possiamo facilmente notare che i primari della sintesi sottrattiva sono uguali ai secondari della sintesi additiva e, inversamente, i primari additivi sono uguali ai secondari sottrattivi.

Si noti che le coppie dei colori complementari sono le stesse in entrambe le sintesi, ma il risultato di miscelare una coppia di luci complementari è ben diverso da quello di miscelare una coppia complementare di sostanze colorate: nel primo caso si ha il bianco, nel secondo un grigio-nero.

La discussione che segue (relativa alla crittografia visuale a colori) effettuerà le miscelazioni di colori con la sintesi sottrattiva (in quanto le share sono dei lucidi da sovrapporre) e verranno considerati soltanto tre colori : il rosso, il verde e il blu. Tutti gli altri colori possono essere ricavati mediante opportune combinazioni di questi tre colori fondamentali.
Dunque, un qualsiasi colore c verrà considerato come una tripla (r,g,b), dove r,g e b indicano, rispettivamente, la quantità e l'intensità di rosso, verde e blu che caratterizzano c.
D' altra parte, si può anche immaginare che la tripla (r,g,b) referenzi tre filtri che, corrispondentemente, assorbono i fotoni relativi al rosso, al verde e al blu. Il valore assunto da ogni elemento nella tripla è approssimato da un intero appartenente all'intervallo [0,255].

Risulta evidente che:
 

c=(0,0,0) corrisponde al colore nero, poiché la luce viene completamente assorbita dai tre filtri;
c=(255,255,255) corrisponde al colore bianco, in quanto la luce non è assorbita in alcuna percentuale;
c=(255,0,0) corrisponde al rosso, dato che i fotoni relativi a tale colore sono gli unici a non essere assorbiti;
c=(100,0,0) corrisponde ad un rosso più scuro, poiché viene assorbita una percentuale dei fotoni relativi al rosso.

Si osservi inoltre che, se le componenti della tripla relativa a c sono tutte di uno stesso valore x, allora il colore ottenuto corrisponde ad un grigio, la cui intensità dipende appunto da x.

Si supponga di avere un pixel di colore c1=(r1,g1,b1) su di un lucido, ed un pixel di colore c2=(r2,g2,b2) su un altro lucido; considerata bianca la luce inziale, il colore c, del pixel ottenuto sovrapponendo i due lucidi, è definito dal seguente operatore di somma per la sovrapposizione di colori:

4.2 Schemi di crittografia visuale a colori (CVCS)

Si consideri che il segreto S consista di un immagine di c colori {x1,...,xc}, quindi ogni pixel in S sarà di uno di questi colori. All'atto della codifica di S, ogni pixel segreto è rappresentato con m sottopixel, ed una share risulta essere una particolare assegnazione di colori a questi sottopixel. Il colore di un sottopixel è scelto nell'insieme {x1,...,xc} U {NERO,BIANCO}; di conseguenza una share può essere considerata come un vettore di m elementi nel suddetto insieme.

Per la rappresentazione di n share, si può ricorrere ad una matrice di dimensione n x m, dove, per l'appunto, ogni riga corrisponde ad una share. Con tale matrice il dealer è in grado di individuare una possibile distribuzione delle share ad n partecipanti; infatti si può pensare che all'i-esimo partecipante venga data la i-esima riga della matrice.

Per semplicità di trattazione, in futuro si indicherà l'insieme {x1,...,xc} con {1,...,c}. Considerato un vettore V di colori, il peso di Hamming generalizzato per i, indicato con Hi(V) per i=1,...,c, corrisponde al numero di elementi in V uguali ad i.

Siano h ed l due interi tali che 0  l < h  m; uno schema di crittografia a c colori (c-CVCS) è definito da c insiemi C1,...,Cc di matrici n x m, i cui elementi sono valori in {1,...,c} U {NERO,BIANCO}, che soddisfano le seguenti proprietà:

1. considerato un insieme qualificato X  Q, per ogni matrice M scelta in Ci (per i {1,...,c} ) si ha che Hi(SOMMA(MX))  h e Hj(SOMMA(MX))  l, per qualunque j diverso da i. In altri termini, sovrapponendo, con l'operatore di somma, le righe della matrice ottenuta dalla restrizione di M rispetto ad X (cioè la matrice MX), il peso di Hamming del vettore risultante assume un valore tale da permettere di distinguere il colore i da tutti gli altri.
2. considerato un insieme non qualificato Y  F, la collezione Di={ MY | M  Ci} di matrici di dimensione |Y| x m, con i=1,...,c contiene matrici uguali. In altri termini, l'insieme delle matrici |Y| x m, ottenute dalla restrizione di M rispetto ad Y, è tale che, dalla sovrapposizione delle righe dei suoi elementi, non si ha alcuna informazione addizionale per distinguere il colore i dagli altri.

Bisogna infine osservare che la qualità di un CVCS è comunque misurata in termini dei parametri m (l'espansione del pixel) ed  (il contrasto). Inoltre il contrasto è definito dall'espressione (h-l)/(h+l), ed assume valore massimo pari ad 1 quando l è uguale a zero e h è uguale a m.