Algoritmi di approssimazione

Abbiamo visto che il SimpleReversalSort non dà luogo a soluzioni ottimali. Gli algoritmi ottimali sono infatti sconosciuti per molti problemi, di modo che gli informatici spesso trovano un compromesso attraverso l’uso di algoritmi di approssimazione che producono una soluzione approssimata piuttosto che una ottimale. La percentuale di approssimazione di un algoritmo A su input π è:

dove A(π) è la soluzione prodotta dall’algoritmo A e OPT(π) è la soluzione ottimale del problema.

La percentuale di approssimazione dell’algoritmo A è definita come la sua massima percentuale di approssimazione su tutti gli input di grandezza n. Per l’algoritmo A che minimizza l’obiettivo (algoritmo di minimizzazione):

Per l’algoritmo di massimazione:

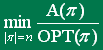
in effetti un algoritmo di approssimazione dà lo scenario del caso peggiore di quanto lontano il risultato di un algoritmo può essere da un ipotetico algoritmo perfetto. La percentuale di approssimazione di un SRS è almeno (n-1)/2 così il biologo non ha alcuna certezza che questo algoritmo arrivi in qualche punto vicino alla soluzione corretta. Per esempio se n è 1001 questo algoritmo può arrivare ad una serie di inversioni che può essere grande 500 volte come l’ottimale.

Il nostro scopo è individuare algoritmi di approssimazione che garantiscano performance migliori, per esempio, un algoritmo con una percentuale di approssimazione di 2 o anche meglio di 1,01. Certo un algoritmo con una percentuale di approssimazione pari a 1 (per definizione un algoritmo corretto e ottimale) sarebbe l’acme della perfezione, ma tali algoritmi sono difficili da trovare. Al momento il miglior algoritmo conosciuto per riordinare le inversioni ha una performance garantita.