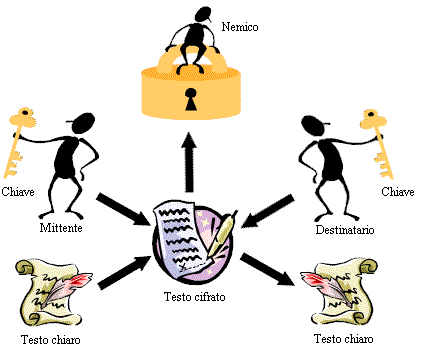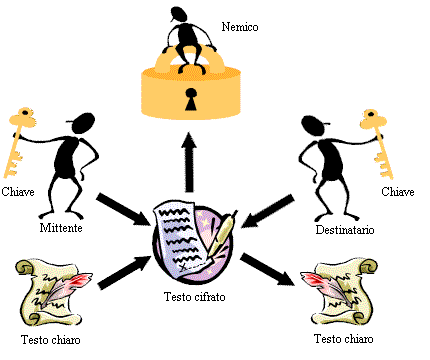
Per migliaia di anni re, regine e generali hanno avuto il bisogno di comunicazioni efficienti per governare i loro paesi e comandare i loro eserciti. Nel contempo, essi compresero quali conseguenze avrebbe avuto la caduta dei loro messaggi in mano ostili: informazioni preziose sarebbero state a disposizione delle nazioni rivali e degli eserciti nemici. Fu il pericolo dell'intercettazione da parte degli avversari a promuovere lo sviluppo di codici, tecniche di alterazione del messaggio destinate a renderlo comprensibile solo alle persone autorizzate.
Una delle prime tecniche di comunicazione segrete, basata sull'occultamento del messaggio, si chiama steganografia, dalle parole greche steganós, che significa coperto, e gráphein, che significa scrivere. Negli anni sono state impiegate in tutto il mondo innumerevoli forme di steganografia.
Uno dei metodi più bizzarri per trasmettere le informazioni segrete era utilizzato nell'antica Persia e viene raccontato da Erodoto. Esso consisteva nel rapare i capelli di uno schiavo e nel scrivergli il messaggio sulla testa. Lo schiavo si recava poi dal destinatario del messaggio dopo che gli erano ricresciuti i capelli e il messaggio era recuperato rapandoglieli nuovamente.
Nell'antica Cina si dipingeva il messaggio su striscioline di seta finissima, che venivano appallottolate e coperte di cera. Le palline erano quindi inghiottite dal messaggero. Nel XVI secolo lo scienziato italiano Giambattista Della Porta spiegò come comunicare tramite un uovo sodo, preparando un inchiostro con 30 grammi di allume in mezzo litro d'aceto, e usandolo per scrivere sul guscio.La soluzione penetra nel guscio, che è poroso, senza lasciar traccia, e tinge l'albume solidificato; quest'ultimo potrà essere letto sbucciando l'uovo.
La longevità della steganografia dimostra che essa garantisce una certa sicurezza, ma il suo punto debole è evidente: se il latore del messaggio è attentamente perquisito, è probabile che il messaggio sia scoperto; in tal caso, il nemico può farne l'uso che crede. In altre parole, la segretezza è perduta nel momento stesso dell'intercettazione. In tal caso è inevitabile che molti messaggi siano trovati.
Perciò in parallelo con lo sviluppo della steganografia si assisté all'evoluzione della crittografia, dal greco kryptós, che significa nascosto. La crittografia non mira a nascondere il messaggio in sé, ma il suo significato. Per rendere incomprensibile un testo, lo si altera per mezzo di un procedimento concordato a suo tempo dal mittente e dal destinatario. Questi può quindi invertire il procedimento, e ricavare il messaggio originale. Il vantaggio della crittografia è che anche se il nemico intercetta il messaggio, esso risulta incomprensibile e quindi inutilizzabile. Infatti il nemico, non conoscendo il procedimento di alterazione, dovrebbe trovare difficile, se non impossibile, ricostruire il significato.
Non tutte le società antiche svilupparono forme di crittografia. La Cina, per esempio, l'unica civiltà antica ad usare una scrittura ideografica, non ne ha mai viste. Le ragioni, a detta degli storici, sono legate alla natura prevalentemente orale delle comunicazioni.
In India, invece, forme di crittografia furono concretamente praticate. In diversi testi sacri sono presenti riferimenti a forme di scritture segrete. Nell'Artha-Sastra, un testo classico sugli affari di stato, si sottolinea l'importanza delle scritture segrete nei servizi di spionaggio. Esempi di scritture segrete sono presenti anche nel Latila-Vistara, un libro che esalta le virtù di Budda.
Nel Kama-Sutra, invece, tra le 64 arti (yogas) che la donna deve conoscere e praticare c'è l'arte della scrittura segreta. La 44-esima e, in particolare, la 45-esima arte (mlecchita-vikalpa) trattano di regole di trasformazione delle parole basate essenzialmente sulla sostituzione di caratteri del messaggio originale.
Anche nelle scritture cuneiforme sviluppate in Mesopotamia sono stati ritrovati esempi di crittografia. Sia presso gli Assiri che i Babilonesi, le due grosse civiltà sorte sulle sponde del Tigri, è stata rinvenuta l'usanza di sostituire le parti terminali delle parole con elementi corti e stereotipati detti colofoni. In Iraq, nel periodo finale delle scritture cuneiformi, è presente per la prima volta la sostituzione di nomi con numeri.
Anche se la steganografia e la crittografia sono discipline indipendenti, possono essere impiegate per alterare e occultare il medesimo testo, garantendo un livello di sicurezza molto più alto. Per esempio, il « microdot », cioè la riduzione di uno scritto alle dimensioni di un punto, è una forma di steganografia che ebbe largo impiego durante la seconda guerra mondiale. Tramite un procedimento fotografico, gli agenti tedeschi in America latina trasformavano una pagina scritta, precedentemente crittografata, in una macchia con un diametro inferiore al millimetro, che poteva essere nascosta nel puntino di una « i » in una comunicazione banale. Il primo microdot fu scoperto dall' FBI nel 1941 grazie a una soffiata.
Anche
oggi l'obiettivo fondamentale della crittografia è quello di consentire che due
o più persone possano trasmettersi messaggi attraverso un canale pubblico (non
sicuro) in modo tale che, anche se un nemico li intercetta, non è in grado di
comprenderli. La crittografia utilizza strumenti propri della teoria della
complessità, teoria degli algoritmi, teoria dell'informazione, teoria dei
numeri, studiando tecniche che permettono di mascherare il linguaggio in modo
da renderlo inintelligibile a chi non possieda un'opportuna "chiave"
di lettura.
Definizione 1 :
Un Crittosistema è una quintupla
(P; C; K; E; D)
con le seguenti
proprietà:
1.
P è un insieme finito dei
possibili testi in chiaro
2.
C è un insieme finito dei possibili testi cifrati
3.
K, lo spazio delle chiavi, è un insieme di possibili chiavi
4.
Per ogni k Î K c'è una funzione di cifratura ek Î E e una corrispondente funzione di
decifratura dk Î D.
ek: P -> C e dk: C -> P
sono tali che dk(ek(x))=x per ogni testo in chiaro x Î P.
x = x1 x2 .... xn
per qualche intero n ³1, dove ogni simbolo del testo in chiaro xi Î P, 1 £ i £ n. Ogni xi è cifrato usando la regola di cifratura ek specificata dalla predeterminata chiave k. Quindi, Alice calcola yi = ek(xi), 1£ i £ n, e la risultante stringa cifrata
y = y1 y2 .... yn
è spedita sul canale pubblico. Quando Bob riceve y1y2....yn
lo decifra usando la funzione di decifratura dk , ottenendo
l'originale testo in chiaro x1x2 .... xn.
Chiaramente, la funzione di cifratura ek è una funzione iniettiva perché
altrimenti la decifratura potrebbe avvenire in modo ambiguo. Per esempio,
se y = ek(x1) = ek(x2)
dove x1¹x2, allora Bob non ha modo di
sapere se y, decifrato, fornisce x1 oppure x2. Notiamo
che se P = C segue che ogni funzione di cifratura è una permutazione, nel senso che il testo
cifrato è ottenuto come permutazione dei caratteri del testo in chiaro.
1.
Ogni funzione di cifratura ek ed ogni funzione di decifratura dk
devono essere calcolabili efficientemente.
2. Un nemico, guardando la stringa cifrata y, non deve essere capace di determinare la chiave k usata per la cifratura, oppure la stringa del testo in chiaro x.
Un’assunzione da fare è che il nemico conosce sempre l'algoritmo di
cifratura ma non la chiave.
1)
per trovarsi nel caso peggiore
2) perché i sistemi che saranno presi in considerazione possono essere utilizzati da utenti diversi, pertanto è improbabile che l'algoritmo possa restare segreto.

|
Figura 2.1: Il mittente applica la chiave al testo in chiaro ottenendo il testo cifrato o crittogramma. Il nemico può anche intercettare il crittogramma durante la trasmissione al destinatario, ma non dovrebbe essere in grado di decifrarlo. Il destinatario, invece, conoscendo la chiave usata dal mittente può ripristinare il testo in chiaro. |
3 Breve storia della crittografia

|
Le più antiche notizie sicure sono probabilmente quelle sulla scitala lacedemonica , data da Plutarco come in uso dai tempi di Licurgo (IX sec a.C.) ma più sicuramente usata ai tempi di Lisandro(verso il 400 a.C.) . Consisteva in un bastone su cui si avvolgeva ad elica un nastro di cuoio; sul nastro si scriveva per colonne parallele all'asse del bastone, lettera per lettera, il testo segreto. Tolto il nastro dal bastone, il testo vi risultava trasposto in modo regolare ma sufficiente per evitare la comprensione senza un secondo bastone uguale al primo. Tra il 390 e il 360 a.C. venne compilato da Enea il tattico, generale della lega arcadica, il primo trattato di cifrari il cui XXI capitolo tratta appunto di messaggi segreti. In questo viene descritto un disco sulla zona esterna del quale erano contenuti 24 fori, ciascuno dei quali era contrassegnato da una lettera disposte in ordine alfabetico. Un filo, partendo da un foro centrale, si avvolgeva passando per i fori delle successive lettere del testo. Il destinatario del messaggio svolgeva il filo dal disco segnando le lettere da esso indicate. Il testo si doveva poi leggere a rovescio. |
|
|
Figura 3.2: Disco di Enea il tattico |
||
|
Figura 3.1: Scitala lacedomonica
|
Il metodo ATBASH
Fonti preziose di scritture segrete sono i testi sacri. Nel Vecchio Testamento gli storici hanno evidenziato tre tipi di trasformazione: l'Atbash, l'Albam e l'Atbah. L'Atbash ebraico è una tecnica di trasformazione ad alfabeto capovolto: il primo carattere dell'alfabeto viene sostituito con l'ultimo, il secondo con il penultimo e così via. Infatti la prima lettera dell'alfabeto ebraico (Aleph) viene cifrata con l'ultima (Taw), la seconda (Beth) viene cifrata con la penultima (Shin); da queste quattro lettere è derivato il nome di Atbash (A con T, B con SH) per questo codice. L'Atbash viene utilizzato nel libro del profeta Geremia per cifrare il nome della città di Babilonia.
Usando l'attuale alfabeto ordinario, l'Atbash può essere riassunto con la seguente tabella di cifratura:
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
|
z |
y |
x |
w |
v |
u |
t |
s |
r |
q |
p |
o |
n |
m |
l |
k |
j |
i |
h |
g |
f |
e |
d |
c |
b |
a |
Quindi il messaggio “Il Libro di Geremia” diviene :
|
Messaggio: |
I |
l |
L |
i |
b |
r |
o |
d |
i |
G |
e |
r |
e |
m |
i |
a |
|
TestoCifrato: |
R |
o |
O |
r |
y |
i |
l |
w |
r |
T |
v |
i |
v |
n |
r |
z |
L'Albam richiede che l'alfabeto venga diviso in due parti e che ogni lettera venga sostituita con la corrispondente dell'altra metà. Infine, l'Atbah richiede che la sostituzione soddisfi una relazione di tipo numerico. Le prime nove lettere dell'alfabeto vengono sostituite in modo tale che la somma della lettera da sostituire e della lettera sostituente risulti uguale a dieci. Quindi, per esempio, Aleph (prima lettera dell'alfabeto) viene sostituita con Teth (nona lettera dell'alfabeto). Per le restanti lettere dell'alfabeto deve valere una regola simile con somma pari a 28 in decimale (per esempio, la 13-esima lettera viene sostituita con la 15-esima, etc.).
Polibio
Lo storico greco Polibio (~200-118 a.C.), nelle sue Storie (Libro X) descrive un interessante metodo di cifratura. L'idea è quella di cifrare una lettera con una coppia di numeri compresi tra 1 e 5, in base ad una matrice 5x5, contenente le lettere dell'alfabeto. Ogni lettera viene rappresentata da due numeri, guardando la riga e la colonna in cui essa si trova. Per esempio, a=11 e r=42. Polibio suggeriva di mandare tanti messaggeri quanti erano i caratteri del messaggio. Questi portavano nella mano sinistra un numero di torce pari all'indice di riga e nella mano destra un numero pari all'indice di colonna. In effetti più che di un codice segreto, si tratta di un sistema di telecomunicazione, di fatto un telegrafo ottico. Telegrafi a torce esistevano da molti secoli ed erano stati descritti da Enea il tattico intorno al 350 a.C., ma erano basati su un limitato elenco di messaggi possibili; quello di Polibio si basa invece sulla scomposizione del messaggio nelle singole lettere ed è quindi in grado di trasmettere qualsiasi messaggio.
|
# |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
1 |
a |
b |
c |
d |
e |
|
2 |
f |
g |
h |
i |
j |
|
3 |
kq |
l |
m |
n |
o |
|
4 |
p |
r |
s |
t |
u |
|
5 |
v |
w |
x |
y |
z |
Nell'alfabeto greco ci sono 24 lettere ed avanza quindi un carattere che Polibio proponeva di usare come segnale di sincronizzazione (inizio e fine trasmissione). Nell'esempio seguente si utilizzerà, al posto di quello greco, l'alfabeto internazionale il quale ha viceversa il difetto di essere formato da 26 caratteri; così per poter costruire il quadrato necessario per la cifratura bisognerà "fondere" due lettere rare nella stessa casella, in questo caso la k e la q. Si otterrà così la tabella a lato.
Ogni lettera può venire quindi rappresentata da due numeri, guardando la riga e la colonna in cui la lettera si trova. Per esempio, a=11 e r=42. Quindi la frase "Attenzione agli scogli" dopo la cifratura risulterà:
|
A |
t |
t |
e |
n |
z |
i |
o |
n |
e |
a |
g |
l |
i |
s |
c |
o |
g |
l |
i |
|
1 1 |
4 4 |
4 4 |
1 5 |
3 4 |
5 5 |
2 4 |
3 5 |
3 4 |
1 5 |
1 1 |
2 2 |
3 2 |
2 4 |
4 3 |
1 3 |
3 5 |
2 2 |
3 2 |
2 4 |
Il cifrario di Cesare
Svetonio nella Vita dei dodici Cesari, un'opera del II secolo d.C., racconta che Giulio Cesare usava per le sue corrispondenze riservate un codice di sostituzione molto semplice, nel quale ogni lettera del testo veniva sostituita dalla lettera che la segue di tre posti nell'alfabeto. Ad esempio la lettera A è sostituita dalla D, la B dalla E e così via fino alle ultime lettere che sono cifrate con le prime come nella tabella che segue (che fa riferimento all'odierno alfabeto internazionale).
| Chiaro |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| Cifrato |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
Prendendo come esempio la frase "Auguri di buon compleanno" si otterrà il seguente messaggio cifrato:
| Chiaro |
a |
U |
G |
U |
R |
I |
D |
I |
B |
U |
O |
N |
C |
O |
M |
p |
L |
E |
A |
N |
N |
O |
| Cifrato |
D |
X |
J |
X |
U |
L |
G |
L |
E |
X |
R |
Q |
F |
R |
P |
S |
O |
H |
D |
Q |
Q |
R |
Più in generale si definisce codice di Cesare un codice nel quale la lettera del messaggio chiaro viene spostata di un numero fisso di posti, non necessariamente tre; un esempio è il codice che sempre secondo Svetonio era usato da Augusto, dove ogni lettera era sostituita da quella immediatamente successiva, e cioè la A dalla B, la B dalla C, e così via.
Poiché l'alfabeto internazionale è composto da 26 caratteri sono possibili 26 codici di Cesare diversi dei quali uno (quello che comporta uno spostamento di zero posizioni) darà un testo cifrato uguale al messaggio iniziale.
In questo periodo la crittografia viene usata solo per celare i nomi propri, sostituendo ogni lettera con quella che la segue nell'alfabeto (per esempio A con B, B con C ecc.). Verso l'anno mille compaiono i primi alfabeti cifranti. Essi sono usati successivamente soprattutto nelle missioni diplomatiche tra i vari staterelli europei, particolarmente da parte delle repubbliche marinare e dalla corte papale di Roma a partire dal XIV secolo.

|
Un sistema usato dall'Arcivescovo di Napoli, Pietro di Grazia, tra il 1363 e il 1365, é quello in cui le lettere sono cifrate con numeri o simboli speciali.La corrispondenza tra lettere e simboli o numeri per la sostituzione è fissata da una tabella. Dagli inizi del XIV secolo, per depistare i tentativi di analisi statistica delle frequenze, si iniziano ad usare più segni per cifrare le vocali, dato che queste sono molto ricorrenti in un testo. Successivamente tale tecnica viene estesa anche alle consonanti più ricorrenti. Inoltre alcune parole, utilizzate frequentemente, (Papa, et, con, quo, etc.) sono sostituite con un solo simbolo. Un primo esempio di questa cifratura fu la lettera di Michele Steno scritta nel 1411, riportata qui a fianco. |
3.3 Crittografia nel
XV secolo
Leon Battista Alberti
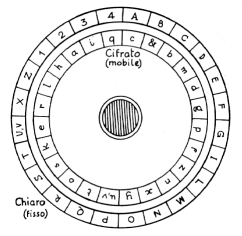
Leon Battista Alberti, nel suo Trattato, ha proposto un disco composto di due cerchi concentrici di rame. Uno esterno fisso di diametro maggiore sul quale sono riportate le lettere dell'alfabeto in chiaro e uno interno mobile per le lettere dell'alfabeto cifrante. Il disco esterno è composto di 24 caselle contenenti 20 lettere maiuscole in ordine lessicografico, escluse H, J, K, W, Y, al posto delle quali ci sono i numeri 1, 2, 3, 4. Il disco interno riporta le 24 lettere minuscole in maniera disordinata (la u e la v sono collassate) ed un simbolo speciale &.
|
Fissata una lettera maiuscola come chiave, ad esempio B, si deve spostare il disco mobile interno in modo da far corrispondere la B con un simbolo particolare del disco interno(&). Si stabilisce in tal modo un'associazione tra le lettere dell'alfabeto in chiaro e quello dell'alfabeto cifrante. Può anche essere utilizzata una chiave diversa per ogni parola del testo in chiaro. Le lettere che di volta in volta corrispondono ai numeri 1 2 3 4 non vengono usate per la cifratura. Tutte le lettere del messaggio da cifrare sono cambiate in base all'associazione tra le lettere maiuscole e quelle minuscole. Tale disco non ottenne successo anche per la decisione dell'Alberti di tenerlo segreto (il suo trattato fu pubblicato solo un secolo più tardi a Venezia insieme ad altri suoi "opuscoli morali" e passò quasi inosservato). |
|
|
Testo in chiaro |
C |
I |
V |
E |
D |
I |
A |
M |
O |
S |
T |
A |
S |
E |
R |
A |
|
Testo cifrato |
b |
f |
e |
d |
m |
f |
c |
n |
y |
s |
k |
c |
s |
d |
o |
c |
3.4 Crittografia nel XVI secolo
Giovan Battista Bellaso
Il bresciano Giovan Battista Bellaso pubblicò tra il 1553 e il 1564 tre opere di crittologia contenenti alcuni cifrari polialfabetici di notevole interesse.
L'idea su cui si basa il principale cifrario proposto dal Bellaso è quella di ricavare cinque alfabeti da una parola segreta convenuta. Le lettere dell'alfabeto vengono scritte in una tabella composta da due righe. In particolare quelle della parola segreta sono inserite nelle prime colonne intercalate sulle due righe e le rimanenti lettere dell'alfabeto vengono scritte di seguito. In questo modo si è ottenuto il primo alfabeto derivato. A partire da questo ricaviamo il secondo spostando circolarmente verso destra la seconda riga di una posizione. Applicando lo stesso procedimento al secondo alfabeto, si ricava il terzo alfabeto derivato e così via fino ad ottenerne cinque, ognuno dei quali sarà identificato da un gruppo di quattro lettere. Facendo riferimento sempre al primo alfabeto, le lettere della prima e della sesta colonna identificano il primo alfabeto derivato, quelle della seconda e della settima colonna identificano il secondo alfabeto derivato. In generale le quattro lettere che identificano l' i-esimo alfabeto sono quelle dell' i-esima e della (i + 5)-esima colonna. A questo punto si deve convenire una frase segreta; le lettere di quest'ultima servono a selezionare l'alfabeto da usare. In particolare, presa l'i-esima lettera della parola segreta, si controlla quale dei cinque identificativi degli alfabeti la contiene. Si determina così l'alfabeto da usare per l'i-esima parola del testo in chiaro. Se il numero di lettere della frase segreta è minore del numero di parole del testo da cifrare, la frase segreta viene riapplicata ciclicamente per la selezione degli alfabeti. La cifratura si effettua sostituendo la lettera del testo in chiaro con la lettera che si trova sulla stessa colonna nell'alfabeto predeterminato.
Riportiamo un esempio: data la parola chiave IOVE, il primo alfabeto derivato(alfabeto latino di 20 lettere, posta V=U) è:
|
I |
O |
A |
B |
C |
D |
F |
G |
H |
L |
|
V |
E |
M |
N |
P |
Q |
R |
S |
T |
X |
Il secondo si ottiene spostando circolarmente la seconda riga:
|
I |
O |
A |
B |
C |
D |
F |
G |
H |
L |
|
X |
V |
E |
M |
N |
P |
Q |
R |
S |
T |
e così via fino ad ottenere cinque alfabeti.
Le quattro lettere che identificano il primo alfabeto sono IDVQ, quelle della prima e della sesta colonna del primo alfabeto derivato. Le quattro lettere che identificano il secondo alfabeto sono OFER, quelle della seconda e settima colonna sempre del primo alfabeto derivato.
| I D V Q | I | O | A | B | C | D | F | G | H | L |
| V | E | M | N | P | Q | R | S | T | X | |
| O F E R | I | O | A | B | C | D | F | G | H | L |
| X | V | E | M | N | P | Q | R | S | T | |
| A G M S | I | O | A | B | C | D | F | G | H | L |
| T | X | V | E | M | N | P | Q | R | S | |
| B H N T | I | O | A | B | C | D | F | G | H | L |
| S | T | X | V | E | M | N | P | Q | R | |
| C L P X | I | O | A | B | C | D | F | G | H | L |
| R | S | T | X | V | E | M | N | P | Q |
A questo punto si deve convenire una frase segreta, per esempio " OPTARE MELIORA"; le lettere di quest'ultima servono a selezionare l'alfabeto da usare.
Volendo allora cifrare la frase "Inviare truppe domani" si ha:
| O P T |
|
Testo in Chiaro I N V I A R E T R U P P E D O M A N I Testo Cifrato X C O X E G A A I C H H D M T D X F S |
Blaise de Vigenére
Blaise de Vigenére pubblicò nel 1586 un trattato di cifrari nel quale proponeva tra gli altri un codice che ebbe grande fortuna e che è ricordato con il suo nome. Si tratta del più semplice codice di sostituzione polialfabetica, e proprio per la sua semplicità ha goduto per secoli di una grossa fama.
La forza del cifrario di Vigenére sta nell'utilizzare non uno ma 26 alfabeti cifranti per cifrare un solo messaggio. Il metodo si può considerare una generalizzazione del codice di Cesare; invece di spostare sempre dello stesso numero di posti la lettera da cifrare, questa viene spostata di un numero di posti variabile, determinato dalle lettere della parola chiave, da concordarsi tra mittente e destinatario. La parola è detta chiave, per il motivo che, essendo in genere molto più corta del messaggio, deve essere ripetuta molte volte. Per maggiori approfondimenti si guardi il paragrafo riguardante Vigenére nella sezione "Principali Cifrari".
|
Chiave |
C |
H |
I |
A |
V |
E |
C |
H |
I |
A |
V |
E |
C |
H |
I |
A |
V |
E |
C |
H |
I |
A |
V |
E |
C |
H |
I |
A |
V |
|
Testo in chiaro |
D |
I |
V |
E |
R |
S |
O |
M |
E |
T |
O |
D |
O |
D |
I |
C |
H |
I |
A |
V |
E |
C |
O |
N |
T |
I |
N |
U |
A |
|
Testo cifrato |
F |
P |
D |
E |
N |
W |
Q |
T |
M |
T |
J |
H |
Q |
K |
Q |
C |
C |
M |
C |
C |
M |
C |
J |
R |
V |
P |
V |
U |
V |
3.5 Crittografia nel XIX
secolo
Dalla metà del XIX secolo l'uso della crittografia assume un ruolo determinante nella trasmissione di messaggi di carattere logistico e strategico. Con l'invenzione della radio i messaggi sono trasmessi anche via etere e quindi esposti molto più di prima all'intercettazione da parte del nemico; il ricorso alla crittografia diventa inevitabile, come la necessità di cifrari sempre più sofisticati. Una necessità che è ignorata in Italia dove si dovrà attendere l'entrata in Guerra nel 1915 per rendersi conto del ritardo accumulato in campo crittografico, e porvi rimedio.
Thomas Jefferson
Il cifrario di Jefferson prende il nome dal suo inventore Thomas Jefferson (1743-1826), uno degli autori della Dichiarazione d'Indipendenza e Presidente degli USA nel 1801-1804. Jefferson non lo mise mai in uso e il suo cifrario fu dimenticato fino al 1922, quando fu riscoperto e utilizzato, fino agli anni '50, dall'esercito statunitense. E nel 1890 Etienne Bazeries un crittologo francese propose l' "Indecifrabile ", un cifrario del tutto equivalente a quello di Jefferson.
|
|
Il codice di Jefferson è un metodo di cifratura meccanico basato su un cilindro di circa 15 cm di lunghezza e 4 cm di larghezza. Il cilindro è costituito da 36 dischi, imperniati su di un asse, in grado di ruotare liberamente. Ogni disco riporta le 26 lettere dell'alfabeto sul bordo esterno, in un ordine differente l'uno rispetto all' altro. Inoltre i dischi possono volta per volta essere inseriti sull'asse in un ordine differente per ogni cifratura, previo accordo tra mittente e destinatario. La cifratura di un messaggio avviene nel seguente modo: il messaggio viene prima di tutto diviso in blocchi di 36 caratteri. Per ogni blocco, i dischi della macchina vengono ruotati in modo tale da far comparire allineati su una riga i caratteri del blocco. Una volta effettuata tale operazione, si sceglie a caso un'altra riga, e si considera la corrispondente sequenza di 36 lettere come il messaggio cifrato. Il ricevente, che possiede un cilindro identico a quello del trasmittente, non deve far altro che ruotare i dischi in modo tale da far comparire il cifrato allineato su una riga. Compiuta questa operazione, deve analizzare le restanti righe. Una sola di queste è una frase di senso compiuto rappresentante il messaggio in chiaro. Una variante è quella di fissare a priori la riga su cui sarà possibile trovare il messaggio in chiaro.
cifrato ->5 GKRPXAFYEQYFUUAXYYEPSQYFTAELCIXVFCKZ
4 HJQOWBHXDPXETRZYAZDORPXESZDMBHWUEBHX
3 IBPNVCQWBOWDSQYZPACNQPWDRYCNZGVTDAGW
2 JNOMUDLTHNVCRPXAIBBMPNVCQWBOYFUSAZFU
1 KONLTHNVCABVNTHNVCALNVCLHXDPXETRZYDP
chiaro -> LAMISSIONEINPOLINESIAEFALLITAXXXXXXX
|
Il cilindro di Jefferson è il primo esempio di una serie di macchine cifranti basate su cilindri e dischi ruotanti intorno ad un asse, la più celebre di tutte è la cosiddetta Macchina Enigma usata dai Tedeschi nella Seconda Guerra Mondiale.
Friedrich Kasiski
Un appassionato della crittografia che diede un notevole contributo alla decifratura dei messaggi, fu Friedrich Kasiski (1805-1881), un ufficiale prussiano che pubblicò un trattato crittografico in cui illustrava una tecnica per demolire il cifrario di Vigenére. Kasiski fornì un metodo per individuare la lunghezza della chiave. Osservò che due porzioni identiche del testo in chiaro vengono cifrate allo stesso modo solo se la porzione di chiave atta a cifrarli è la stessa per entrambe. Quindi, se troviamo due porzioni identiche del testo cifrato, ciascuna di lunghezza almeno tre, allora ci sono buone probabilità che esse corrispondano a pezzi identici del testo in chiaro.
Il test di Kasiski cerca le coppie di porzioni identiche nel testo cifrato di lunghezza almeno tre e memorizza la distanza tra le posizioni iniziali delle due porzioni. Se si ottengono le distanze d1, d2, ..., allora si può dedurre che la lunghezza della chiave divida il massimo comune divisore dei di. Il limite di questo metodo è che fornisce solo la probabile lunghezza della chiave e non il suo valore. Una volta stabilita la lunghezza della parola chiave, il crittoanalista può decomporre il testo cifrato in tante sottosequenze quante sono le lettere della chiave e analizzarle singolarmente dato
che ogni sottosequenza è cifrata attraverso un semplice cifrario a sostituzione circolare.
Auguste Kerckoffs von Nieuwenhof
Nello stesso periodo, in Francia, Kerckoffs (1835-1903) scriveva un trattato dal titolo "La cryptographie militaire" in cui venivano enunciati i principi a cui doveva rispondere un metodo di cifratura per essere considerato valido.In tale esposizione, per la prima volta, si asserisce che un sistema deve mantenere la sua impenetrabilità, anche se l'avversario conosce nei dettagli il modo in cui il sistema si applica, purché non sia a conoscenza della chiave usata. Praticamente la sicurezza di un cifrario poggia esclusivamente sulla chiave segreta e non sul metodo di cifratura usato. Questo stesso principio, al giorno d'oggi, è alla base della valutazione di ogni metodo di cifratura che viene proposto.
Playfair cipher
Il Playfair cipher fu inventato dal noto fisico Sir Charles Wheatstone (1802-1875), ma il nome di Playfair deriva da colui che ha divulgato nelle alte sfere governative questo metodo di cifratura. Lyon Playfair, barone di St.Andrews, mostrò per la prima volta questo sistema nel 1854 durante una cena organizzata da Lord Granville alla presenza di Lord Palmerston (1784-1865) allora ministro degli Esteri. La speranza di Playfair era quella di far utilizzare il Cipher durante la guerra di Crimea ma il sistema fu effettivamente utilizzato dall'esercito britannico solamente a partire dalla guerra Boera. Il Cipher è ritenuto essere il primo metodo di cifratura a bigrammi (coppie di caratteri). Si usa una matrice di 25 lettere che viene riempita nelle prime caselle con la parola chiave, abolendo le eventuali lettere ripetute, ed è completata con le rimanenti lettere nel loro ordine alfabetico. Si omette la W che, se necessario, potrà essere cifrata come una doppia V. Così, con la chiave computer, si otterrà la tabella dell'esempio.
La cifratura si farà nel seguente modo:
| C | O | M | P | U |
| T | E | R | A | B |
| D | F | G | H | I |
|
J | K | L | N | Q |
| S | V | X | Y | Z |
|
Il testo in chiaro deve essere diviso in bigrammi di due lettere consecutive. Le due lettere si cercano sul quadrato e si sostituiscono con altre secondo le seguenti regole: se le due lettere chiare si trovano su una stessa riga, si prendono le due lettere che le seguono a destra; se una delle due lettere chiare si trova sulla quinta colonna a destra, si prenderà la prima lettera a sinistra della stessa riga. Se le due lettere chiare sono sulla stessa colonna, si prendono le due lettere sottostanti; se una lettera è nell'ultima riga, si prenderà la lettera che sta nella prima riga della stessa colonna; se le due lettere sono in colonne e righe diverse, si prendono le due che costituiscono un rettangolo con esse, cominciando da quella che si trova nella stessa riga della prima lettera del bigramma in chiaro; qualora il bigramma chiaro presenti due lettere uguali si cercherà di eliminare questo raddoppio, oppure di romperlo inserendo una lettera rara (k, w, x, y). Prendendo la frase "Inviare subito nuove truppe" si otterrà la seguente successione di bigrammi (si noti che il raddoppio della lettera 'p' è stato spezzato inserendo fra le due lettere la 'Y'). |
| IN VI AR ES UB IT ON UO VE TR UP YP E |
| Quindi, seguendo le regole, il messaggio cifrato risultante sarà il seguente: |
| HQ ZF AB TK BI DB PK CM OF EA CU AY E |
3.6 Crittografia nel XX secolo
Dopo che la Gran Bretagna dichiarò guerra alla Germania il 3 settembre 1939, le operazioni di decifrazione Britanniche furono spostate da Londra a Bletchley Park. Tra il 4 settembre 1939 e l'estate del 1944, Alan Turing (1912-1954) (uno dei più famosi matematici di questo secolo, fra i fondatori dell'informatica teorica) alloggiò al Crown Inn, a Shenley Brook End, un villaggio vicino Bletchley. Il lavoro eseguito da Alan Turing e dai suoi colleghi a Bletchley Park poté essere completamente apprezzato solo molti anni dopo, quando cadde il segreto militare sulle tecniche di crittoanalisi durante la guerra. Quasi tutte le comunicazioni tedesche venivano cifrate con una macchina chiamata Enigma. Questa macchina è una nobile rappresentante dei cifrari a rotore, utilizzati fino all'introduzione di cifrari elettronici e microelettronici che hanno sconvolto e trasformato il mondo della crittografia. Per "rompere" Enigma (alcuni dettagli della soluzione sono tenuti segreti fino ad oggi) Turing, per conto del governo inglese, si servì di gigantesche macchine chiamate appunto Colossi, che possono considerarsi i precursori dei moderni calcolatori elettronici. Turing è autore di ricerche estremamente importanti sul concetto logico-matematico di calcolabilità: lo strumento che egli ha proposto per affrontare il problema è noto oggi col nome di macchina di Turing. Una delle prime macchine di cifratura a rotori è stata costruita dal californiano Edward Hebern, che la brevettò nel 1921. Autentici gioielli della crittografia meccanica sono le macchine costruite da Boris Hangelin; nel 1927 egli aveva rilevato una ditta che produceva materiale crittografico e che ancora oggi è prospera e fiorente, anche se ormai i rotori sono entrati nei musei della scienza. Per rendersi conto di quanto i tempi siano cambiati basterà ricordare che l'Enigma aveva un grande inconveniente: era sprovvisto di stampante. I risultati apparivano illuminati su una tastiera apposita, lettera dopo lettera, e una persona doveva provvedere a trascriverli a mano su un foglio di carta. Una stampante elettro-meccanica avrebbe appesantito troppo il congegno e lo avrebbe reso poco maneggevole.
Analizziamo adesso i cifrari che sono stati più utilizzati nel corso dei secoli e che oggi conservano esclusivamente valenza storica.
In
questi sistemi di cifratura, ogni simbolo del testo in chiaro viene trasformato
in un simbolo dell'alfabeto del testo cifrato. I segni di punteggiatura e gli
spazi non vengono cifrati, in modo tale che il testo diventa un'unica stringa
di caratteri alfabetici. Questi cifrari si dividono in due categorie:
monoalfabetici e polialfabetici. Nei monoalfabetici, ogni carattere, una volta
sostituito con un altro carattere, conserverà tale sostituzione durante tutta
la fase di cifratura; per esempio, se la parola “bacca” sarà cifrata in
“efggf”, allora la lettera 'a' sarà sempre cifrata con la 'f ', la 'c' con la 'g' e così via. Nei sistemi
polialfabetici, invece, lo stesso carattere può essere cifrato con più caratteri. Un esempio di cifrario a sostituzione monoalfabetica è quello di Cesare. Nei cifrari che vedremo l'alfabeto sarà di 26 caratteri posti in
corrispondenza biunivoca con gli interi da 0 a 25 come mostrato nella seguente tabella:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
In
questo cifrario la chiave é una coppia di interi in Z26
K = (a,b) con a,b Î Z26
Dato un messaggio x da cifrare, la funzione di cifratura é del tipo
ek
(x) = (ax + b) mod 26
Queste funzioni sono
dette funzioni affini, da cui il nome del cifrario. Vediamo sotto quali
condizioni una funzione di questo tipo va bene per la cifratura. Come abbiamo
già detto, una funzione di cifratura deve essere iniettiva; se così non fosse il ricevente non potrebbe decifrare il messaggio in modo univoco. Pertanto la chiave (a,
b) deve essere scelta in modo che
l'equazione y = (ax + b) mod 26 abbia un'unica soluzione.
Vediamo un esempio. Supponiamo di scegliere come chiave la coppia a = 2 e b = 0 e che il messaggio cifrato sia y = 0; allora la funzione di cifratura é
ek (x) = 2x
e
quindi per decifrare il messaggio l'equazione da risolvere è
2x = 0 mod 26
Le soluzioni sono x = 0 e x = 13, quindi due messaggi in chiaro distinti corrispondono allo stesso messaggio cifrato. Di conseguenza la scelta a = 2 non è ammissibile perché vogliamo che la congruenza
ax = 0 mod 26 (1)
abbia un'unica soluzione per x. Sia d = gcd(a,26). Allora la congruenza (1) ha almeno due distinte soluzioni in Z26, cioè x = 0 e x = 26/d. Per avere un'unica soluzione deve essere gcd(a,26) = 1, cioè a deve essere primo con 26. Tale condizione è necessaria e sufficiente affinché ek(x) risulti iniettiva.
Teorema 1 : ax=y mod 26 ha un’unica soluzione per ogni y se e solo se gcd (a, 26) = 1.
Dimostrazione : Supponiamo
che ax=y mod 26 abbia un'unica soluzione per ogni y e supponiamo per assurdo che gcd(a, 26) = d >1. Risolvendo
l'equazione per y = 0 giungiamo ad un assurdo; infatti ax = 0 mod 26 ha due soluzioni distinte in Z26 : x
= 0 e x = 26/d . Quindi
Sia gcd(a, 26) = 1, siano x1 e x2 soluzioni distinte di ax = y mod 26 quindi
ax1 = ax2
mod 26
da cui
a(x1 - x2 ) = 0 mod 26
quindi
26 | a( x1 - x2 )
x1 = x2
mod 26
così x1 e x2 sono la stessa soluzione.
Calcoliamo la funzione di decifratura d applicata ad un messaggio cifrato y. Siccome
y = ax + b mod 26
si
ha che
y -b = ax mod 26
da
cui
a-1 (y-b) mod 26 = x
quindi
d(y)
= a-1 (y - b) mod 26.
Il numero di possibili chiavi per il cifrato affine è dato dal numero di coppie (a,b), tali che b può assumere qualsiasi dei 26 possibili valori mentre a solo i valori tra 0 e 25 primi con 26. Quindi il numero dei possibili valori che a può assumere è dato dalla cardinalità di Z*26, che può essere determinata tramite la funzione di Eulero:
f(26) = (13-1) (2-1) = 12
Pertanto
il numero di possibili chiavi è 26x12 , troppo basso per scoraggiare una
ricerca esaustiva.
Il cifrario di Vigenére è un ottimo esempio di cifrario a sostituzione di tipo polialfabetico ed è dovuto agli studi di Blaise de Vigenére, che visse nel diciassettesimo secolo. Sia m un intero positivo fissato. Definiamo P = C = K = (Z26)m. Per una chiave k = (k1; k2; .. ; km ) Î (Z26 ) m definiamo la funzione di cifratura come
ek (x1; x2; …. ; xm ) = (x1+k1; x2 + k2;…. ; xm + km )
e quella di decifratura come
dk(y1; y2; … ; ym ) = (y1- k1; y2 – k2;
….. ; ym - km)
dove
tutte le operazione sono fatte in Z26.
Utilizzando
la corrispondenza A«0, B«1, …, Z«25, possiamo associare ogni chiave k con
una stringa alfabetica di lunghezza m. L'idea del cifrario è di codificare m
caratteri alfabetici alla volta : il messaggio viene partizionato in blocchi di
m caratteri e ogni blocco è cifrato con la stessa chiave. Ai blocchi di n <
m caratteri vengono aggiunti i mancanti m-n in modo arbitrario. Lo spazio delle chiavi è 26m.
Questo cifrario è stato ritenuto sicuro per circa 2 secoli, in quanto la chiave
non è costituita solo dai valori ki , ma anche dal numero delle
chiavi m. Quindi bisogna determinare prima il numero di sottochiavi e poi il
valore di ciascuna. Per semplicità vediamo la cifratura con un esempio.
Esempio1: Supponiamo di
voler cifrare il messaggio ATTACCOALLALBA con la chiave SALERNO. Si procede in questo modo: si divide il
messaggio in gruppi di sette lettere e
si cifrano i due gruppi che si ottengono con la chiave. La caratteristica di
questo metodo è che due lettere uguali
del messaggio in chiaro possono essere cifrate in modo differente, infatti:
|
messaggio in chiaro |
A |
T |
T |
A |
C |
C |
O |
A |
L |
L |
A |
L |
B |
A |
|
chiave |
S |
A |
L |
E |
R |
N |
O |
S |
A |
L |
E |
R |
N |
O |
|
messaggio cifrato |
S |
T |
E |
E |
T |
P |
C |
S |
L |
W |
E |
C |
O |
O |
Come
si può vedere, le due T sono cifrate con caratteri differenti. Per facilitare i
conti veniva utilizzata una tabella di 26 righe e di 26 colonne in cui si
ricercavano le coppie (carattere del testo in chiaro-carattere della chiave),
rispettivamente come indici di riga e di colonna. Per esempio la prima A di ATTACCO e la S di SALERNO, si trovano rispettivamente sulla prima
riga e sulla diciannovesima colonna: il carattere del testo cifrato è S.
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
|
| a |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| b |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
| c |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
| d |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
| e |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
| f |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
| g |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
| h |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
| i |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
| j |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
| k |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
| l |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
| m |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
| n |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| o |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
| p |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
| q |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
| r |
r |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
| s |
s |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
| t |
t |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
| u |
u |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
| v |
v |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
| w |
w |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
| x |
x |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
| y |
y |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
| z |
z |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
Questo cifrario è tanto più resistente agli attacchi crittoanalitici quanto più lunga è la chiave.
Crittoanalisi: frequenze delle lettere
In realtà anche un insieme di chiavi molto grande non garantisce la sicurezza del cifrario. La crittoanalisi è la disciplina che studia come forzare i cifrari, cioè come determinare la chiave che è stata utilizzata per cifrare i messaggi. Molte tecniche di crittoanalisi utilizzano proprietà statistiche dei linguaggi naturali. Il problema nasce dal fatto che le strutture dei linguaggi naturali posseggono delle asimmetrie frequentistiche intrinseche che possono essere sfruttate per "rompere" i cifrari a sostituzione. Precisamente, le parole di un linguaggio non sono stringhe casuali dell'alfabeto. Piuttosto, esistono caratteri più frequenti di altri. Le vocali 'a' ed 'e', per esempio, ricorrono più spesso delle consonanti 'v' e 'z'. A partire da una stima delle frequenze dei caratteri singoli dell'alfabeto nelle parole di un linguaggio, dei bigrammi (coppie di caratteri) e dei trigrammi (triple di caratteri) è possibile, procedendo per tentativi, individuare la permutazione che è stata usata nella cifratura. Ovviamente, le frequenze delle lettere dipendono dal tipo di testo considerato.
Esistono tavole che riportano le frequenze di ciascun carattere di ciascun testo. Nella lingua italiana, per esempio la lettera "E" è la più frequente, seguita dalla "I". Un esempio di tavola delle frequenze, calcolate su di un testo di 1000 caratteri, è la seguente:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|
103 |
9 |
43 |
38 |
126 |
8 |
20 |
11 |
116 |
0 |
0 |
66 |
26 |
66 |
87 |
32 |
6 |
67 |
61 |
61 |
30 |
15 |
0 |
0 |
0 |
9 |
Due tecniche che sono state utilizzate in passato per alterare le frequenze consistono nell'introduzione di particolari simboli : omofoni e nulle. L'idea alla base degli omofoni è la seguente: individuare quali sono le lettere maggiormente ricorrenti, ampliare l'alfabeto cifrante aggiungendo un certo numero di extra-simboli, ed effettuare la cifratura dei caratteri più frequenti con più di un carattere, fissati al momento della scelta della sostituzione. Per esempio, se si stabilisce di sostituire la lettera 'a' con 'f' e '!', il cifrante potrà sostituire 'a' una volta con 'f' e un'altra con '!', scegliendo a caso tra uno dei due. In questo modo, la frequenza del simbolo che cifra la 'a' è pressappoco dimezzata, divisa tra quella di 'f' e quella '!'. Quindi gli omofoni permettono di abbassare le frequenze delle lettere più comuni.
Le nulle sono simboli che servono per alzare la frequenza delle lettere meno ricorrenti. L'idea, in questo caso, è semplicemente quella di aggiungere nel messaggio in chiaro le lettere meno frequenti in posizioni tali da non inficiare la comprensione del messaggio originale, alzando, nello stesso tempo, la frequenza delle corrispondenti lettere.
Il
cifrario di Hill è un altro
crittosistema polialfabetico e fu inventato nel 1929 da Lester Hill. Sia m un
intero positivo, definiamo P = C = (Z26)m.
L'idea
è di costruire m combinazioni lineari contenenti ognuna m caratteri alfabetici
del testo in chiaro e produrre, con ciascuna combinazione lineare, un singolo
elemento del testo cifrato. La chiave utilizzata in questo cifrario è una
matrice K invertibile di dimensione m * m. Per x = (x1,…, xm )Î P e KÎ K,
calcoliamo y = ek (x) = (y1 ,…, ym ) come segue:
)).gif)
Poniamo le virgole all'interno di un vettore per distinguere gli elementi.
Usando
la notazione matriciale: y = xK
Diciamo che il testo cifrato è ottenuto dal testo in chiaro per mezzo di una trasformazione lineare, di blocchi di m caratteri. In ultimo vediamo come avviene la decifratura, cioè come x può essere calcolato a partire da y . Chiaramente, si dovrà usare la matrice inversa K-1 per cui il testo in chiaro x si otterrà come
x = yK-1
Esempio 2:
Supponiamo che la chiave sia
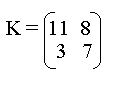
Poiché
la chiave è una matrice 2x2 dobbiamo cifrare il messaggio in blocchi di due
caratteri. Supponiamo che il messaggio da cifrare sia CASA. Al blocco CA
corrisponde la coppia (2,0) e il testo cifrato è dato da:
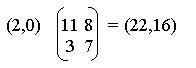
Al
blocco SA
corrisponde la coppia (18,0) e il testo cifrato è dato da
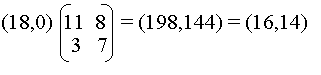
Quindi la cifratura di "CASA" è "WQQO" che corrisponde a (22,16,16,14). Per quanto riguarda la decifratura occorre calcolare l'inversa della matrice K che è:
|
K -1 = |
|
e poi calcolare :
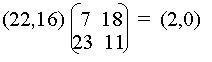
e
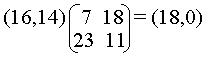
Tutti i crittosistemi che abbiamo discusso finora coinvolgono la sostituzione: caratteri del testo in chiaro sono sostituiti, nel testo cifrato, con caratteri diversi. L' idea di un cifrario a permutazione è di non modificare i caratteri del testo in chiaro, ma di cambiare le loro posizioni. Formalmente, sia m un intero positivo fissato. Sia P = C = (Z26)m e sia K l'insieme di tutte le permutazioni di {1, …,m}. Data una chiave p (permutazione), definiamo la funzione di cifratura come
ep (x1, …. , xm ) = ( xp(1) , … , xp(m) )
e
la funzione di decifratura come
dp (y1 , …. , ym ) = ( yp -1(1) , … , yp -1(m) )
dove p-1
è la permutazione inversa di p .
Esempio 3
Sia ATTACCOALLALBAX il messaggio da cifrare e la permutazione (2,3,1) la nostra chiave. Questo significa che:
p(1) = 2 p(2)
= 3 p (3) = 1
La
chiave scelta ci dice di dividere il testo in chiaro in gruppi di tre caratteri
e di permutarli nell'ordine stabilito, cioè la prima lettera occuperà il
secondo posto della tripla, la seconda lettera il terzo posto, la terza il
primo. Per esempio, per la prima tripla ATT, avremo TAT.
Così procedendo il messaggio cifrato sarà: TATCACLOAALALXBA.
Notiamo che il numero di chiavi disponibili con questo metodo è m!, quante sono le possibili permutazioni di m caratteri. I cifrari a permutazione sono un caso particolare del cifrario di Hill. Data una permutazione p dell'insieme {1, ….. , m}, possiamo infatti definire la matrice delle permutazioni Kp= (ki,j) di dimensioni m x m in accordo alla formula
k i, j = 1 se j = p(i) altrimenti k i,j = 0
La matrice di permutazione è una matrice in cui ogni riga e ogni colonna contiene
esattamente un “1” e tutti gli altri valori sono “0”.
Riconsiderando l'Esempio 3, la matrice Kp che si ottiene è:
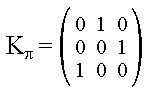
Analogamente al cifrario di Hill, per decifrare il messaggio, dobbiamo calcolare l' inversa della matrice di permutazione che chiamiamo K-1p .
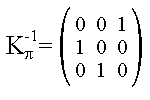
Questo
sistema fa uso di una matrice 5 x 5, che rappresenta la chiave, in cui ci sono
25 lettere distinte dell'alfabeto disposte in ordine arbitrario. L'unica
lettera non presente è la Q, in quanto è la lettera che è quasi sempre seguita dalla U e quindi facilmente riconoscibile. Ogni
lettera individua ed è individuata dal suo numero di riga e dal suo numero di
colonna. Il testo in chiaro deve essere di lunghezza pari, dovrà essere diviso
in coppie di caratteri e ciascuna coppia deve avere caratteri distinti. Nel caso
in cui il testo sia di lunghezza dispari si aggiunge un carattere fittizio che
non alteri il senso del messaggio, per ottenere la parità. Analogo stratagemma
si utilizza se una delle coppie ha i due caratteri uguali: si inserisce come
secondo carattere uno che non altera la comprensione del testo. Con queste
caratteristiche ogni coppia di caratteri rientra sicuramente in uno fra questi
tre casi:
1. Le due lettere della coppia si trovano sulla stessa riga.
2.
Le due lettere si trovano sulla stessa colonna.
3.
Le due lettere non si trovano né sulla stessa riga né sulla stessa colonna.
La cifratura è eseguita su una coppia di lettere per volta. Ogni coppia del testo in chiaro rientra in uno dei tre casi precedenti, ciascuno dei quali va trattato in modo differente:
|
W |
H |
I |
S |
K |
|
Y |
A |
B |
C |
D |
|
E |
F |
G |
J |
L |
|
M |
N |
O |
P |
R |
|
T |
U |
V |
X |
Z |
|
1. Le lettere
della coppia del testo in chiaro vanno cifrate con le lettere che le seguono sulla
stessa riga (con la convenzione “circolare” che l'ultima lettera della riga sia
seguita dalla prima). Per esempio per la coppia WI si ha HS, WH diventa HI, etc. . |
|
2. Le lettere
della coppia del testo in chiaro vanno cifrate con le lettere immediatamente
sottostanti (sempre con la convezione “circolare”) ; ad esempio IG diventa BO e VB
diventa IG. |
|
3. In questo caso, che è il più frequente, le due lettere individuano sulla matrice un “rettangolo” di cui due vertici rappresentano la coppia di caratteri del messaggio in chiaro e gli altri due i corrispondenti caratteri del messaggio cifrato. La convezione che si utilizza nella cifratura è che la prima lettera del testo risultante é quella che si trova sulla stessa riga della prima lettera della coppia in chiaro. Per esempio, NC diventa PA, mentre CN diventa AP. |
La chiave di questo cifrario è la matrice di lettere, che costituisce una chiave difficile da ricordare. Una modifica a tale cifrario atta ad ovviare a tale difficoltà è la seguente: gli utenti che vogliono comunicare si accordano su una frase da ricordare a memoria, la prima occorrenza di ogni lettera nella frase è inserita nella matrice, le lettere dell'alfabeto che non compaiono nella frase sono inserite successivamente in ordine lessicografico. Per esempio se la frase fosse: “cogli l'attimo fuggente”, la matrice sarebbe quella riportata sotto. Alcune varianti del cifrario utilizzano matrici 3 x 9 oppure 4 x 6.
|
C |
O |
G |
L |
I |
|
A |
T |
M |
F |
U |
|
E |
N |
B |
D |
H |
|
J |
K |
P |
R |
S |
|
V |
W |
X |
Y |
Z |
Nei crittosistemi studiati fino ad ora successivi elementi del testo in chiaro sono cifrati mediante la stessa chiave k, cioè la stringa cifrata y è ottenuta nel modo seguente:
y = y1 y2 …. = ek (x1
) ek (x2 ) ….
Crittosistemi di questo tipo sono spesso definiti “cifrari a blocchi”. Un approccio alternativo consiste nell'utilizzare gli “stream cipher”. L'idea di base consiste nel generare una sequenza, detta “keystream”
z = z1 z2 .......
e nell'utilizzarla per cifrare la stringa
x = x1 x2 ……
del testo in chiaro nel modo seguente
![]()
dove
zi
= fi ( k, x1 , …. , x i -1 )
L’elemento zi della sequenza è utilizzato per cifrare xi, ossia
![]()
Pertanto per cifrare la stringa x1
x2 ….. bisogna calcolare
z1, y1, z2, y2 …..
Analogamente per decifrare la stringa y1 y2 …..bisogna calcolare
z1, x1, z2, x2 ......
Per
esempio se P = C = K = Z26 le funzioni di cifratura e decifratura possono essere le seguenti:
yi = xi + zi mod 26
xi = yi - zi mod 26
Gli stream cipher sono spesso definiti in termini binari, cioè P = C = K = Z2. In tal caso le funzioni di cifratura e decifratura possono essere le seguenti:
yi = xi + zi mod 2
xi =
yi - zi mod 2
Se associamo a "0" il valore booleano "falso", ed a "1" il valore booleano "vero" allora l'addizione modulo 2 corrisponde allo XOR, pertanto la cifratura e la decifratura possono essere implementate molto efficientemente in hardware.
Un metodo per generare la sequenza keystream a partire da m valori k1 , . . . . , km consiste nel fissare i valori per z1, .…., zm come z i = k i per ogni i = 1,……, m, e nel calcolare i valori successivi in base ad una relazione di ricorrenza lineare di grado m :
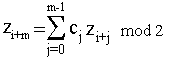
dove c0,….,cm-1 Î Z2 sono costanti predeterminate. Tale ricorrenza è funzione lineare dei termini precedenti, ed ha grado m perché ciascun termine dipende dagli m precedenti. In tal caso la chiave consiste dei 2m valori ( k1……km ; c0 ......cm-1 ), dove ki=zi per i = 1,….., m.
Esempio 4
Supponiamo che sia m = 4 e che la keystream sia generata nel modo seguente:
z i+4 = z i + z i+1 mod 2, dove i ³ 1.
Se ad esempio si considerano i seguenti
valori iniziali: 1, 0, 0, 0 la keystream corrispondente è
1, 0, 0, 0, 1, 0, 0, 1, 1, 0,…..
Un
altro aspetto interessante di questo metodo è che la keystream può essere
generata in hardware in modo molto efficiente utilizzando un feedback shift
register. Consideriamo un registro con
m stadi. Il vettore (k1 ,……, km ) viene usato per l' inizializzazione.
Ad
ogni istante vengono effettuate contemporaneamente le seguenti operazioni:
1.
k1 si presenta come nuovo bit della keystream ;
2.
k2 ,……, km vengono shiftati a sinistra di un posto;
3.
viene calcolato il nuovo valore di km , che è :
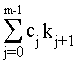
Osserviamo che il
feedback lineare è portato avanti attraverso certi stadi del registro (come
specificato dalle costanti cj che assumono valore “1” ) e viene computata una somma modulo 2
(che corrisponde ad uno XOR ).
Questo cifrario può essere considerato un caso particolare dello Stream cipher in cui la sequenza degli z i è calcolata nel modo seguente:
zi = ki per i £ m, zi = xi-m, per i>m.
Le funzioni di cifratura e decifratura sono le seguenti:
yi = xi+zi mod26
xi= yi - zi mod26
Vediamo come realizzare ciò,attraverso un esempio
Esempio 5
Supponiamo
di voler cifrare il messaggio ATTACCOALLALBA
con la chiave SALERNO: dopo aver cifrato la prima parte con la
chiave SALERNO,
anziché riutilizzarla come accade in Vigenére, si procede con la cifratura
utilizzando il messaggio in chiaro come continuazione della chiave.
|
Messaggio in chiaro |
A |
T |
T |
A |
C |
C |
O |
A |
L |
L |
A |
L |
B |
A |
|
Chiave |
S |
A |
L |
E |
R |
N |
O |
A |
T |
T |
A |
C |
C |
O |
|
Messaggio cifrato |
S |
T |
E |
E |
T |
P |
C |
A |
E |
E |
A |
N |
D |
O |
Intorno al '500 si diffuse l'uso dei nomenclatori. Un nomenclatore è essenzialmente un cifrario a sostituzione che si serve di omofoni e di simboli aggiuntivi per rappresentare/cifrare alcuni dei termini più comuni nella corrispondenza. Solitamente, l'alfabeto del cifrato è diverso da quello in chiaro: ogni lettera dell'alfabeto in chiaro può essere sostituita con una tra diverse lettere dell'alfabeto cifrato. Inoltre, come dicevamo, a parole frequenti corrispondono simboli specifici. Tali simboli, oltre che cifrare le relative parole, permettono anche di ridurre la lunghezza della comunicazione.
L'idea del cifrario a dizionario per molti versi è simile a quello dei nomenclatori ed, in particolare, all'uso di simboli predefiniti per rappresentare parole frequenti. In questo caso, i due comunicanti condividono un dizionario diviso in due colonne: nella prima sono riportate le parole del testo in chiaro, mentre nella seconda sono presenti quelle del cifrato (dizionario a lista semplice). L'operazione di cifratura consiste nel sostituire le parole della prima colonna con le corrispondenti della seconda. L'operazione di decifratura richiede la sostituzione inversa. Naturalmente, se le righe del dizionario sono ordinate rispetto alle parole della prima colonna, la decifratura risulta lunga e tediosa. Pertanto, spesso i cifrari a dizionario sono divisi in due metà (dizionario a lista doppia). Nella seconda, le righe sono ordinate rispetto alle parole della seconda metà. Per avere un'idea, si pensi ad un dizionario bilingue odierno (italiano - inglese, inglese - italiano). Il vantaggio di questo cifrario è che il messaggio sembra una frase comune e non un messaggio cifrato; lo svantaggio risiede nella “grandezza” della chiave: un libricino.
Supponiamo
che il messaggio in chiaro sia ATTACCO ALL'ALBA. Per cifrare questo
testo si può anche pensare di ottenerne un altro che comunque abbia senso
compiuto, come ad esempio vediamoci
a pranzo.
Nel
1917 il signor Gilbert Vernam, impiegato della compagnia AT&T, inventò un ingegnosissimo sistema di protezione crittografica,
per comunicazioni su telegrafo, dei testi codificati in binario. Egli costruì
per prima cosa un dispositivo in grado di leggere contemporaneamente due nastri
in input e generare a partire da essi un nastro di output tale che ciascun foro
fosse generato mediante uno XOR dei due corrispondenti fori sui nastri
input. Dopodiché prese un nastro su cui era perforata una sequenza di caratteri
casuale ed un nastro su cui era perforato un testo reale e li passò nella sua
macchina. Il risultato fu un nastro completamente inintellegibile, ovvero
cifrato.
Lo
schema di crittografia di Vernam è uno schema one-time pad; un tale schema
richiede che:
1.
la chiave sia usata
una sola volta (da qui il nome),
2.
deve essere lunga
almeno quanto il testo in chiaro,
3.
fra i bit che
compongono la chiave non deve esserci alcuna relazione,
4. la chiave deve essere
generata casualmente.
In pratica se il testo in chiaro è X = 0110 e la chiave è K = 1100, applicando il metodo di Vernam otteniamo il seguente testo cifrato:
Y = X Å K = 1010
la decifratura si ottiene nel seguente modo:
X = Y Å K = 0110
Notiamo
che abbiamo applicato la stessa chiave ed effettuato la stessa operazione sia
per la cifratura che per la
decifratura, ciò caratterizza un sistema crittografico reversibile, questo è uno dei molti aspetti notevoli del cifrario di Vernam. Per ciò che concerne la
sicurezza, a tutt'oggi, questo è l'unico metodo ad essere perfetto, ossia
costituisce un cifrario assolutamente indecifrabile in senso stretto.
Un
cifrario si dice perfetto se, dati X il testo in chiaro e Y il cifrato corrispondente, gode della seguente proprietà:
per ogni X’e Y’ risulta:
Pr ( X = X’ ) = Pr (X = X’ | Y = Y’ ). (2)
La
proprietà di cui sopra si chiama sicurezza perfetta.
Le proprietà che caratterizzano il one-time pad sono estremamente restrittive, volendole rispettare si ottiene un sistema scomodo da usare in pratica, considerando che le ingombranti chiavi andrebbero generate in anticipo rispetto al loro uso previsto, e conservate in luogo sicuro. Sono questi i motivi per cui questo sistema non viene usato che per casi eccezionali, come la famosa hot-line tra Washington e Mosca.
Un'altro
problema è che il one-time pad è modificabile; un intruso può cambiare Y così che il messaggio M decifrato sia differente dal messaggio
spedito. Non ci sono modi per il destinatario di controllare che il mittente
abbia spedito proprio il messaggio ricevuto. Ci sono delle varianti che possono
evitare di utilizzare delle chiavi così grandi, ma che fanno perdere la
perfezione al sistema perché introducono delle dipendenze statistiche. Un
esempio è quello di prendere una chiave in un grosso testo, come la Bibbia,
specificando un punto di inizio qualunque, tutti i caratteri da quel punto in
poi, formeranno la chiave. La dipendenza statistica è insita proprio nel fatto
che le parole devono avere senso compiuto. La difficoltà per i
crittoanalisti, oltre alla conoscenza
della chiave (punto di inizio nel testo),
sta anche nel capire qual è il
testo utilizzato.
Il problema con le chiavi corte, che dunque devono essere riutilizzate ciclicamente nel corso del messaggio, è che producono, in uscita, delle regolarità statistiche che possono essere usate dai crittoanalisti per forzare il cifrario.
Ragionando con i moderni termini della teoria dell'informazione, si
comprende come la “somma” di una chiave casuale ad un testo in chiaro annulli
l'ordine intrinseco nel testo stesso, producendo un cifrario a sua volta
casuale, nel quale l'entropia H, che rappresenta la
quantità di informazione contenuta in un messaggio X, è massima.
Definizione 2 :
L'entropia H(X) di una variabile aleatoria X
con distribuzione di probabilità p1 , p2 , ……, pm , è uguale a
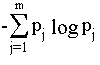
e definisce la quantità di informazione contenuta in X.
In termini di entropia è possibile definire un sistema di cifratura come segue: sia X la variabile aleatoria associata al messaggio in chiaro, sia Y la variabile aleatoria associata al messaggio cifrato e sia K la variabile aleatoria associata alla chiave, tutte con distribuzione di probabilità arbitraria. Con questa definizione la (2) si può scrivere:
H ( X ) = H ( X | Y )
Affinché le tre variabili aleatorie X, Y, K realizzino un sistema crittografico perfetto si deve avere:
|
1. Cifratura: il testo cifrato è univocamente
determinato dal testo in chiaro e dalla chiave. Formalmente : |
|
H ( Y | XK ) = 0 |
|
2. Decifratura: il testo in chiaro è univocamente determinato dal testo
cifrato e dalla chiave. Formalmente : |
|
H ( X | YK ) = 0 |
|
3. Sicurezza perfetta: la conoscenza del testo cifrato non dà alcuna informazione sul testo in chiaro. Formalmente: |
|
H ( X | Y ) = H ( X ) |
Teorema 2 : In un sistema crittografico con sicurezza perfetta, la lunghezza della chiave deve essere tanto grande quanto quella del messaggio in chiaro.
Dimostrazione : Supponiamo che X sia il messaggio in chiaro,Y il messaggio cifrato e che la chiave utilizzata sia K.
La
mutua informazione I ( KX | Y ) può essere scritta come
I ( KX | Y ) = H ( K | Y ) - H ( K | XY )
oppure come
I ( KX | Y ) = H ( X | Y ) - H ( X | YK )
da cui otteniamo :
H ( K | Y ) = H ( K | XY ) + H ( X | Y ) - H ( X | YK ) (3)
H ( K | Y ) = H ( X | Y ) + H ( K | XY ) (4)
In
più, dato che l'incertezza sulla chiave è più grande dell'incertezza che
si ha sulla chiave conoscendo anche il messaggio cifrato Y, cioè
|
H ( K ) |
³ H ( K | Y ) |
|
= H ( X | Y ) + H ( K | XY ) per la (4) |
|
| = H ( X ) + H ( K | XY ) per la sicurezza perfetta | |
| ³ H ( X ) siccome H(K|XY)³0 |
Ciò significa che l'incertezza che si ha sulla chiave è maggiore o uguale della incertezza che si ha sul messaggio X. Se supponiamo che X sia distribuito uniformemente, allora:
H ( X ) = log |X|
log |K| ³ H ( K ) ³ H ( X ) = log |X|.
Alla
fine del XVIII secolo, Thomas Jefferson inventò una macchina cifrante, detta
cilindro di Jefferson che è rimasta in
uso fino alla seconda guerra mondiale. Essa consiste in un cilindro montato su un asse e diviso in 36 dischi
uguali che possono ruotare liberamente attorno all'asse. Sul bordo esterno di ciascun disco sono
scritte le 26 lettere dell'alfabeto, equispaziate l'una dall'altra. L'ordine con cui sono scritte le
lettere non è quello naturale e varia da disco a disco.
Il
messaggio in chiaro va cifrato a blocchi di 36 lettere ciascuno; si compone
tale messaggio ruotando opportunamente i dischi e il messaggio cifrato si
ottiene scegliendo una qualunque delle 25
”righe” rimanenti. Decifrare il messaggio è
facile: basta “scrivere” sul
cilindro il cifrato e scegliere, sulle restanti 25 righe, la frase che ha senso
compiuto. Poiché il cilindro è formato
da 36 dischi, la probabilità di avere più di una frase di senso compiuto è
bassissima. Una variante è quella di
fissare a priori la riga su cui sarà possibile trovare il messaggio in chiaro.
Nello stesso periodo in cui Vernam ideava il suo sistema crittografico, si andava affermando una classe di macchine cifranti basate su principi meccanici o elettromeccanici, le cosiddette macchine a rotori, che rimasero per anni le dominatrici incontrastate della scena crittografica. Lo scambiatore o rotore, uno spesso disco di gomma attraversato da una complessa rete di fili, è la parte più importante di tali macchine. I circuiti interni dello scambiatore determinano il modo in cui un elemento del testo in chiaro è cifrato.
Il
funzionamento di una macchina a rotori è concettualmente molto semplice: esso
si basa su una catena di dischi mobili
(i rotori, appunto) affacciati l'uno sull'altro, ciascuno dei quali costruito di materiale isolante e dotato su
entrambe le facce di 26 contatti elettrici. Ogni contatto di una faccia corrisponde ad uno ed un solo contatto
sull'altra faccia, ma la corrispondenza non è diretta, bensì “incrociata” in
qualche modo. Ad ogni contatto corrisponde un carattere dell'alfabeto.
La cifratura avviene applicando una tensione sul primo rotore al contatto corrispondente al carattere da cifrare. La decifratura avviene similmente, basta applicare una tensione al contatto dell'ultimo rotore, corrispondente al carattere del testo da decifrare. Supponiamo che i dischi siano tre in successione. Applicando una tensione al contatto 1 del primo disco, questi la trasferisce ad un differente contatto del secondo disco per via del suo collegamento elettrico interno, il secondo fa lo stesso con il terzo così che alla fine il contatto alimentato in uscita corrisponde ad una lettera differente da quella applicata all'ingresso. Ora i tre dischi possono ruotare a passi discreti attorno al proprio asse e sono collegati tra loro da un meccanismo, l'odometro, grazie al quale, non appena viene creata la codifica di una lettera del testo in chiaro, l'ultimo disco ruota di 1/26 di giro; ciò ha l'effetto di modificare la struttura cifrante della macchina e quindi, in pratica, le permette di applicare al prossimo carattere una trasformazione differente da quella applicata al carattere precedente. Quando l'ultimo disco ha compiuto un'intera rotazione, quello alla sua sinistra avanza di un passo ed il ciclo riprende, ma con una struttura che non si ripete mai come prima. In pratica dunque, la macchina modifica il suo cifrario ad ogni carattere e non riapplica la stessa trasformazione se non dopo un numero straordinariamente alto di caratteri cifrati. Tra le varie macchine del genere, costruite tra le due guerre mondiali, vi è la tedesca Enigma.
Nel 1918 l'inventore tedesco Arthur Scherbius avendo studiato ingegneria elettrica ad Hannover e Monaco, mise a punto un dispositivo crittografico che in sostanza era una versione elettromeccanica del disco cifrante dell'Alberti. La sua invenzione fu chiamata Enigma. Essa consiste di diversi ingegnosi elementi combinati in un potente e sofisticato dispositivo per la produzione di scritture segrete. La versione semplificata del congegno di Scherbius consiste in 3 componenti collegati da fili elettrici: una tastiera per immettere le lettere del testo in chiaro; un'unità scambiatrice che cifra la lettera trasformandola nel corrispondente elemento del crittogramma (testo cifrato); un visore con varie lampadine, che accendendosi indicano la lettera da inserire nel testo cifrato. Per generare il crittogramma, l'operatore preme il tasto corrispondente alla lettera da cifrare; l'impulso elettrico raggiunge l'unità scambiatrice, e dopo essere stato elaborato va ad illuminare il visore in modo da evidenziare la lettera cifrata corrispondente.
|
|
|
Figura 5.1 : Versione semplificata della macchina Enigma con un alfabeto di sei lettere. L'elemento più importante di Enigma è lo scambiatore. Ogni volta che una lettera è digitata tramite la tastiera e cifrata, lo scambiatore ruota di un posto, cambiando il modo in cui la lettera seguente sarà sostituita. Ad esempio digitando ' b ' sulla tastiera la corrente entra nello scambiatore, segue il percorso dei fili elettrici ed emerge in modo da illuminare la lettera ' a '. Il riquadro a destra riassume il modo in cui ogni elemento dell'alfabeto di sei lettere è cifrato |
Con questo schema di base lo scambiatore in sostanza definisce una corrispondenza tra le lettere del testo in chiaro e quelle cifrate, e la macchina può essere usata per realizzare una semplice cifratura per sostituzione monoalfabetica. Il passo successivo consiste nel far ruotare automaticamente il disco scambiatore di un 1/26 di giro dopo la cifratura di ogni lettera. In altre parole, la corrispondenza tra lettere in chiaro e cifrate cambia dopo la cifratura di ogni lettera cosicché la cifratura di una stessa lettera muta continuamente. Con questa disposizione rotante, lo scambiatore in sostanza definisce 26 diverse corrispondenze tra lettere in chiaro e cifrate, ed Enigma può essere usata per effettuare una cifratura polialfabetica. Tuttavia, così come è il congegno, ha un punto debole evidente; dopo 26 pressioni continue dello stesso tasto, il disco torna alla posizione iniziale, e se si continuasse a premere lo stesso tasto, lo schema di cifratura si ripeterebbe tale e quale. Per ridurre il numero di ripetizioni può essere introdotto un altro scambiatore. In questo modo, ogni volta che una lettera è cifrata, il primo disco ruota di un carattere, mentre il secondo disco invece resta immobile fin quando il primo scambiatore ha completato un giro, solo a questo punto il secondo scambiatore avanza di una posizione.
L'aggiunta del secondo scambiatore comporta il vantaggio che lo schema della cifratura non si ripete finché il secondo scambiatore non è tornato al punto di partenza, il che richiede 26 giri completi del primo scambiatore, ovvero la cifratura di 26x26=676 lettere. Per una sicurezza ancora maggiore viene aggiunto un terzo rotore, per cui il numero di sostituzioni diverse è 26x25x26=16.900 (il secondo rotore effettua una rotazione in meno rispetto agli altri due, poiché dopo aver effettuato un giro completo rimane fermo una volta per far ruotare il terzo rotore). Inoltre viene aggiunto un riflessore molto simile allo scambiatore che consiste in un disco di gomma con circuiti interni che non ruotano e i fili entrano ed escono dallo stesso lato. Col riflessore installato quando si digita una lettera il segnale elettrico attraversa i 3 rotori, raggiunge il riflessore ed è mandato indietro. Quindi il segnale elettrico passa di nuovo nei rotori ma lungo un percorso diverso.
|
|
Figura 5.2 : Il progetto di Scherbius del modello base di Enigma includeva un terzo scambiatore e un riflessore, che costringe l'impulso elettrico ad attraversare di nuovo gli scambiatori. Con questo assetto particolare, la pressione del tasto 'b' determina l'illuminazione di 'a' sul visore.
|
Supponiamo di voler inviare un messaggio cifrato. Prima di cominciare devono essere regolati i rotori in modo che assumano la posizione iniziale voluta. Le posizioni possibili sono 263 = 17.576, quella prescelta determina il modo in cui un messaggio è cifrato.
Per decifrare il testo cifrato, il destinatario deve possedere un'altra macchina Enigma e conoscere l'assetto iniziale dei rotori. Egli batte il testo cifrato lettera per lettera e annota i caratteri del testo in chiaro.
Versione finale della Macchina Enigma
Dato che il numero di chiavi è alto ma non abbastanza per scoraggiare un crittoanalista che può disporre di più macchine e più aiutanti, per accrescere l'affidabilità si dovrebbe aumentare il numero di assetti cioè il numero di chiavi. Invece di aggiungere un altro rotore e aumentare di 26 volte le chiavi sono state introdotte due nuove caratteristiche. Innanzitutto si possono utilizzare rotori removibili e sostituibili, ad esempio il primo e il terzo rotore si possono scambiare di posto. Quindi dati tre elementi intercambiabili essi possono essere permutati in sei modi differenti; con questo accorgimento il numero di chiavi aumenta di un fattore pari a sei. La seconda caratteristica è l'inserimento di un pannello a prese multiple tra la tastiera e il primo rotore. Il pannello permette al mittente di inserire alcuni cavi muniti di spinotti, che aveva l'effetto di scambiare due lettere prima della loro immissione nel rotore. L'operatore di Enigma dispone di sei cavi che gli danno la possibilità di scambiare sei coppie di lettere simultaneamente.
|
|
Figura 5.3 : Il pannello a prese multiple è interposto tra la tastiera e gli scambiatori. Inserendo gli appositi cavetti è possibile scambiare due lettere. Per esempio, un cavo può essere usato per collegare 'b' ed 'a' del pannello, cosicché quando il crittografo decide di cifrare 'b', giunto ai rotori il segnale elettrico seguirebbe il percorso proprio della 'a' e viceversa. L'operatore di Enigma dispone di sei cavi, che gli danno la possibilità di scambiare sei coppie di lettere. Le altre 20 lettere restano non collegate e quindi non scambiate. |
Calcolo del numero di chiavi possibili.
Rotori: i due dischi rotanti più esterni effettuano 26 rotazioni ognuno, mentre quello centrale ne effettua 25, quindi sono ammesse 26x25x26=16.900 combinazioni di orientamenti.
Unità cifratrice: i tre rotori (1,2,e 3) possono essere inseriti nell'unità centrale in diverse posizioni reciproche, così riassumibili: 123, 132, 213, 231, 312, 321. Sono quindi ammesse 6 diverse posizioni reciproche dei rotori.
Pannello a prese multiple: i possibili abbinamenti di 2 x 6 = 12 lettere su 26 sono moltissime, per l'esattezza 100.391.791.500, che si ottiene dalla formula seguente dove p, il numero di cavi, è uguale a 6.
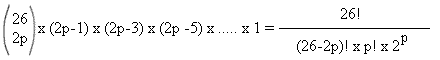
Il numero totale di chiavi si ottiene moltiplicando le suddette possibilità: 16.900 x 6 x 100.391.791.500.
La forza della cifratura di Enigma non dipende dal tener segreto il dispositivo, ma dal tener segreta la chiave, cioè il suo assetto all'inizio della cifratura
L'inventore di Enigma ottenne il primo brevetto nel 1918. La macchina per cifrare era contenuta in una scatola compatta di 34 x 28 x 15 cm e pesava ben 12 chilogrammi.
Utilizzo della machina Enigma
La chiave era specifacata da 3 parametri:
| Assetto del pannello a prese multiple | A/L - P/R - T/D - B/W - K/F - O/Y |
| Disposizione degli scambiatori | 2 - 3 - 1 |
| Orientamento degli scambiatori | Q - C - W |
Per applicare la chiave si deve regolare Enigma nel modo seguente:
Assetto del pannello a prese multiple: Scambio di A e L collegando le prese corrispondenti con un cavetto isolato; scambio di P e R, T e D, B e W, K e F, O e Y, realizzato allo stesso modo.
Disposizione degli scambiatori: collocazione dello scambiatore 2 nel primo alloggiamento all'interno della macchina; collocazione dello scambiatore 3 nel secondo alloggiamento; collocazione dello scambiatore 1 nel terzo alloggiamento.
Orientamento degli scambiatori: Ogni scambiatore aveva un alfabeto inciso sull'anello più esterno, che permetteva di orientarlo in modo preciso rispetto all'asse di rotazione. In questo caso l'operatore avrebbe ruotato lo scambiatore del primo alloggiamento in modo che Q fosse rivolta in alto, quella del secondo alloggiamento in modo che C fosse rivolto in alto, quello del terzo alloggiamento in modo che W fosse rivolta in alto.
|
|
|
[ 2 ] A. Lange e E. A. Soudart, Traité de Cryptographie, Parigi 1925 |
| [ 3 ] Simon Singh, Codici e Segreti, Rizzoli Milano 1999 |
| [ 4 ] Newton, David E., Encyclopedia of Cryptology, ABC-Clio, Santa Barbara 1997. |
| [ 5 ] Smith, Lawrence, Dwight, Cryptography, Dover, New York 1943. |
| [ 6 ] Beutelspacher, Albrecht, Berardi Luigia, Crittologia, Franco Angeli, Milano 1996. |
| [ 7 ] Gaines, Helen Fouché, Cryptanalysis, Dover, New York 1956. |
| [ 8 ] Hodges, Andrew, Storia di Enigma. Vita di Alan Turing, Bollati Boringhieri , Torino 1992. |
| [ 9 ] Khan, David, Seizing the Enigma, Arrow, London 1996. |
| [ 10 ] Harris, Robert, Enigma, Mondadori, Milano 1996. |
| [ 11 ] La genesi della Crittografia: http://www.apogeonline.com/libri/00483/allegati/doc/algoritmi/storia.htm (copia locale) |
| [ 12 ] The German Enigma Cipher Machine http://home.us.net/~encore/Enigma/enigma.html (copia locale) |
| [ 13 ] National Security Agency Enigma http://www.nsa.gov/museum/enigma.html (copia locale) |
| [ 14 ] Alan Turing http://www.computer50.org/mark1/turing.html |
| [ 15 ] Vita di Alan Turing http://www.turing.org.uk/ |
| [ 16 ] Deutsches-museum http://www.deutsches-museum.de/ausstell/meister/e_enigma.htm (copia locale) |
| [ 17 ] On Enigma and a method for its decryption http://www.cs.miami.edu\~harald\enigma\enigma.html (copia locale) |
| [ 18] Codebreaking and Secret Weapons in World War II http://home.earthlink.net\~nbrass1\enigma.htm (copia locale) |