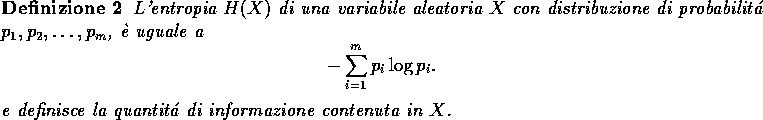
Abbiamo visto nella sezione precedente, come Vernam riuscı a realizzare un cifrario perfetto. Ragionando con i moderni termini della teoria dell'informazione, si comprende come la ``somma'' di una chiave casuale ad un testo in chiaro annulli l'ordine intrinseco nel testo stesso, producendo un cifrario a sua volta casuale, nel quale l'entropia H, che rappresenta la quantitá di informazione contenuta in un messaggio X, è massima.
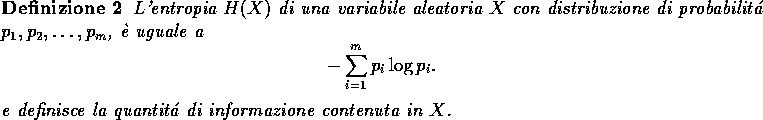
In termini di entropia possiamo definire un sistema di cifratura come segue: sia X la variabile aleatoria associata al messaggio in chiaro, sia Y la variabile aleatoria associata al messaggio cifrato e sia K la variabile aleatoria associata alla chiave, tutte con distribuzione di probabilità arbitraria. Con questa definizione la (3.10) si puó scrivere:
![]()
![]()
Dimostrazione Supponiamo che X sia il messaggio in chiaro che Alice vuole mandare a Bob, che Y sia il messaggio cifrato che Bob riceve e che la chiave utilizzata sia K. Ricordiamo che X, Y e K sono variabili casuali. Affinché le tre variabili realizzino un sistema crittografico perfetto si deve avere :
![]()
![]()
![]()
H(K) ¯Ció significa che l'incertezza che si ha sulla chiave è maggiore o uguale della incertezza che si ha sul messaggio X. Se supponiamo che X sia distribuito uniformemente, allora:
= H(X|Y) + H(K|XY) per la (3)
= H(X) + H(K|XY) per la sicurezza perfetta
siccome
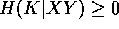
![]()
da cui la lunghezza di K è maggiore o uguale della lunghezza di X, cioé
![]()