Successivo: Calcolo delle S-box Su: Criteri generali d'implementazione Precedente: Criteri generali d'implementazione

Le permutazioni

Per le permutazioni, visto che sono diverse, una prima idea è di utilizzare una funzione che sia in grado di realizzarle tutte (questo è il modo d'agire dell'implementazione Plain Des).

Consideriamo:

• M il vettore che individua la permutazione da effettuare. È costruito dalla tabella corrispondente facendo sí che la i-esima riga della tabella venga inserita nel vettore dopo la (i-1)-esima.
  

  Nel caso di IP

  M= [58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4, 62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8, 57,49,41,33,25,17, 9,1,59,51,43,35,27,19,11,3, 61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7].

  Da M ricaviamo il modo con cui ottenere la sequenza finale a partire da quella iniziale. Nel caso di IP M[1]=58 equivale a dire che il primo bit dell'output è il 58-esimo bit dell'input;

• la sequenza da permutare, di dimensione n. Viene memorizzata in un vettore di char : con costituita da 8 bit. I primi 8 bit della sequenza da permutare sono memorizzati in gli ultimi 8 bit in ;
• d la dimensione della sequenza d'output che viene anch'essa memorizzata in un vettore di char in modo che i primi 8 bit dell'output siano memorizzati in gli ultimi 8 bit in ;

La specificazione di d e l'uso di vettori di char (un char è costituito da 8 bit) per la memorizzazione di e 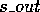, rende la funzione molto flessibile. Infatti grazie a d è posssibile realizzare oltre alle permutazioni IP, e P anche l'espansione E e le riduzioni PC-1 e PC-2 caratterizzate da sequenze d'output che hanno dimensioni differenti dalle sequenze d'input, e grazie all'uso di vettori di char le diverse taglie che e 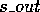possono assumere vengono gestite in modo semplice (per IP e n=d=64, per E n= 32 mentre d=48, per P n=d=32, per PC-1 n=64 mentre d=56 e per PC-1 n=56 mentre d=48, si osserva che la lunghezza delle varie sequenze è sempre multipla di 8 quindi un opportuno vettore di char riesce a memorizzarle sempre).

Lo schema della funzione è il seguente :

I passi (4) e (5) sono composti. Infatti per prelevare il bit r (passo (4)) si devono fare le seguenti operazioni :

1. Individuare il byte in cui è contenuto il k-esimo bit di , è il byte .
2. Individuare la posizione del bit all'interno del byte, è k mod 8.
3. Prelevare il bit k-esimo tramite un and tra l'r-esimo byte è una mask opportuna.

Un discorso analogo vale per inserire il bit x nella sequenza d'output (passo (5)). Si individua il byte in cui occorre inserirlo, la posizione all'interno del byte, quindi si copia il bit x tramite un operazione di or.

Tale metodo risulta essere perømolto costoso, per la realizzazione di IP infatti sono necessarie circa 2500 operazioni (sono le operazioni elementari del linguaggio C compresa l'assegnazione).

Un altra possibilità è avere del codice non flessibile come quello suddetto ma che funzioni per una specifica permutazione. Si puørealizzare il cambiamento di posizione di un bit in questo modo:

  

Con questa tecnica avremo tante istruzioni di questo tipo, tante linee di codice, quanti sono i bit nella sequenza d'output. Si utilizzerà per ciascuna la e lo shift opportuno.

A differenza della prima tecnica descritta, che per essere flessibile ci costringe ad usare i vettori di char per memorizzare le sequenze di bit, con questa tecnica possiamo usare i tipi di dati piú utili, generalmente dei long (un long è 32 bit).

Diamo un esempio di come la tecnica descritta dall'istruzione (1) viene utilizzata effettivamente. Consideriamo la permutazione IP, la realizziamo nel seguente modo:

1. Consideriamo e una coppia di long che contiene i 64 bit su cui si deve applicare la matrice di permutazione IP. e è una coppia di long usata per contere i 64 bit finali. Con riferimento all'istruzione (1) e sono rispettivamente i 32 bit piă sinistra e i 32 bit piă destra della sequenza iniziale x, mentre e sono rispettivamente i 32 bit piă sinistra e i 32 bit piă destra della sequenza finale y;
2. Inizializziamo a zero e : ;
3. Realizziamo M(1)=58 con la linea di codice

   

   Rispetto alla schema generale non abbiamo né lo shift di 58-1=57 posizioni. Questo perché nel nostro caso x e y sono entrambe suddivise in due sottosequenze di 32 bit ciascuna, e per x e e per y. Percui, quando consideriamo l'epressione generale M(k)=t il t-esimo bit di x è inserito come k-esimo bit di se e come (k-32)-esimo bit di se . Anche il valore t è preso con riferimento alle due sequenze di 32 bit e , invece di 58 consideriamo 26 perché il 58-esimo bit di x è il 26-esimo di (26=58-32). Ciøsignifica che consideriamo il t-esimo bit di quando e il (t-32)-esimo bit di quando ;

4. Il secondo scambio che si effettua è M(2)=50, realizzato tramite

   

   Visto che 18=50-32 e dovendo considerare un valore di k=18 lo shift dev'essere di 18-2=16 posizioni.

5. Si continua in questo modo usando o e o in accordo con i valori di k e t, finché la permutazione non è completata.
   

Ogni istruzione di tipo (1) equivale a fare 4 operazioni quindi occorrono 256 operazioni per realizzare IP contro le circa 2500 della tecnica precedente, un guadagno notevole, anche se la realizzazione risulta essere ancora lenta se comparata al numero di operazioni con cui IP è effettuata nelle implementazioni D3Des e Libdes, per entrambe solo 45 operazioni.

Successivo: Calcolo delle S-box Su: Criteri generali d'implementazione Precedente: Criteri generali d'implementazione