


Successivo: Ulteriori considerazioni sul protocollo
Su: Oblivious Transfer
Precedente: Oblivious Transfer
Definiamo innanzitutto con d la percentuale di conteggio oscuro, cioè la probabilità che un detector registri un conteggio durante un lasso
di tempo nel quale nessun fotone è incidente su di esso (quindi, è una probabilità d'errore), e con q l'efficienza quantistica, vale a
dire la probabilità di registrare un conteggio quando un fotone è incidente sul detector (un tipico fotomoltiplicatore può avere
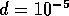 e
e 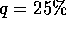 ). Siano, ora,
). Siano, ora, 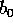 e
e 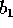 i bit di Alice e sia c la scelta di Bob (cioè Bob vuole ottenere
i bit di Alice e sia c la scelta di Bob (cioè Bob vuole ottenere 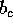 ).
Il protocollo per l'OT è il seguente:
).
Il protocollo per l'OT è il seguente:
- Bob dice ad Alice l'efficienza quantistica q e la percentuale di conteggio oscuro d dei suoi detector. E' necessario adattare il protocollo
alle limitazioni fisiche dell'apparato rilevatore di Bob, se non si vuole compromettere seriamente la probabilità di successo dello stesso.
Se questi valori sono soddisfatti (vedremo che devono essere tali da produrre particolari condizioni), Alice manda successivamente a Bob
l'intensità
 dell'impulso luminoso che vorrà utilizzare, la frazione a di tale impulso che si attende che Bob percepisca
con successo, e la percentuale
dell'impulso luminoso che vorrà utilizzare, la frazione a di tale impulso che si attende che Bob percepisca
con successo, e la percentuale 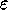 di errore sui bit che sarà disposta a correggere nei dati di Bob, per compensare il suo calcolo
oscuro e le altre sorgenti di rumore. Alice decide anche su un parametro di sicurezza N, usato nel seguito, e lo annuncia a Bob. I due, infine,
si accordano su un codice binario lineare a correzione d'errore capace di correggere, con alta probabilità, parole a N bit trasmesse con
probabilità d'errore
di errore sui bit che sarà disposta a correggere nei dati di Bob, per compensare il suo calcolo
oscuro e le altre sorgenti di rumore. Alice decide anche su un parametro di sicurezza N, usato nel seguito, e lo annuncia a Bob. I due, infine,
si accordano su un codice binario lineare a correzione d'errore capace di correggere, con alta probabilità, parole a N bit trasmesse con
probabilità d'errore 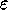 . Osserviamo in particolare che a dovrebbe essere posto normalmente a
. Osserviamo in particolare che a dovrebbe essere posto normalmente a 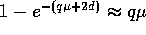 ,
la probabilità di Poisson di rilevare 1 o più fotoni (o anche conteggi oscuri ) in un impulso di intensità
,
la probabilità di Poisson di rilevare 1 o più fotoni (o anche conteggi oscuri ) in un impulso di intensità  , mentre
, mentre 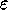 dovrebbe normalmente essere posto a
dovrebbe normalmente essere posto a 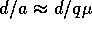 . La scelta di Alice di
. La scelta di Alice di  è guidata dalla necessità di porre simultaneamente
a alto abbastanza ed
è guidata dalla necessità di porre simultaneamente
a alto abbastanza ed 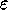 basso abbastanza da fare in modo che le ricezioni di Bob siano meno rumorose e più efficienti.
Mostreremo in seguito che un OT sicuro può essere ottenuto quando
basso abbastanza da fare in modo che le ricezioni di Bob siano meno rumorose e più efficienti.
Mostreremo in seguito che un OT sicuro può essere ottenuto quando
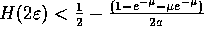 ,
dove H è la funzione entropia.
,
dove H è la funzione entropia. - Alice manda a Bob una sequenza casuale di 2N/a impulsi luminosi, di intensità
 , nelle quattro polarizzazioni canoniche
(rettilinea orizzontale e verticale e diagonale a 45 gradi e a 135 gradi).
, nelle quattro polarizzazioni canoniche
(rettilinea orizzontale e verticale e diagonale a 45 gradi e a 135 gradi). - Bob decide casualmente, per ogni impulso, se misurarlo nella base rettilinea o diagonale e registra le basi e i risultati delle misure
in una tavola, ogni volta che (con probabilità approssimativamente a) percepisce un impulso. Quindi Bob riceverà con successo
approssimativamente 2N impulsi (
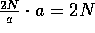 , cioè 2N/a mandati da Alice, moltiplicato per la frazione a di essi che Bob
dovrebbe ricevere). Se egli ne ha ricevuto di più (e ciò può capitare a causa di conteggi multipli), ignora l'eccesso; se ne ha
ricevuto di meno (e ciò può capitare a causa di perdite naturali nel canale quantistico), completa la tavola con entrate casuali,
così da avere esattamente 2N entrate. Bob, infine, dice ad Alice i tempi d'arrivo di tutti i 2N impulsi, ma non le basi che ha usato
per misurarli nè i risultati delle sue misure (ciò assicura Alice che Bob abbia misurato effettivamente gli impulsi).
, cioè 2N/a mandati da Alice, moltiplicato per la frazione a di essi che Bob
dovrebbe ricevere). Se egli ne ha ricevuto di più (e ciò può capitare a causa di conteggi multipli), ignora l'eccesso; se ne ha
ricevuto di meno (e ciò può capitare a causa di perdite naturali nel canale quantistico), completa la tavola con entrate casuali,
così da avere esattamente 2N entrate. Bob, infine, dice ad Alice i tempi d'arrivo di tutti i 2N impulsi, ma non le basi che ha usato
per misurarli nè i risultati delle sue misure (ciò assicura Alice che Bob abbia misurato effettivamente gli impulsi). - Alice rivela a Bob le basi che ha usato per mandare ognuno degli impulsi da lui ricevuti.
- Bob partiziona i suoi impulsi in due insiemi di N impulsi ciascuno: un buon insieme consistente (per quanto è possibile)
di impulsi ricevuti nella corretta base, ed un cattivo insieme consistente di impulsi ricevuti nella base errata. Egli dice ad Alice
gli indirizzi dei due insiemi ma non le dice qual'è il buono o il cattivo insieme.
A questo punto del protocollo Bob condivide con Alice una parola (cioè una stringa a N bit, con un'attesa percentuale d'errore non più
grande di
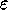 , se ha indovinato per meno di N volte la corretta polarizzazione), corrispondente al suo buon insieme di misure; condivide
niente (o quasi niente, se ha misurato più di N bit nelle corrette basi) riguardo al suo cattivo insieme di misure, supposto che egli segua
fedelmente il protocollo. D'altra parte Alice non sa quale parola condivide con Bob. Vediamo, ora, come Bob possa correggere gli errori occorsi
nel suo buon insieme.
, se ha indovinato per meno di N volte la corretta polarizzazione), corrispondente al suo buon insieme di misure; condivide
niente (o quasi niente, se ha misurato più di N bit nelle corrette basi) riguardo al suo cattivo insieme di misure, supposto che egli segua
fedelmente il protocollo. D'altra parte Alice non sa quale parola condivide con Bob. Vediamo, ora, come Bob possa correggere gli errori occorsi
nel suo buon insieme. - Usando il concordato codice a correzione d'errore, Alice computa le sindromi delle parole corrispondenti ad ogni suo insieme e le
manda a Bob su un canale libero da errori. Da tali sindromi, Bob è in grado di recuperare la parola originale corrispondente al suo
buon insieme, ma non quella corrispondente al suo cattivo insieme (questo per la proprietà di opportuni codici detti codici concatenati,
che sono in effetti quelli scelti per la correzione degli errori). Inoltre, Alice computa un sottoinsieme casuale di parità per
ogni insieme e rivela a Bob gli indirizzi definenti tali sottoinsiemi, ma non le risultanti parità. A questo punto, Bob conosce una
di queste parità esattamente (quella relativa al suo buon insieme), mentre non conosce niente (o quasi niente) circa l'altra parità.
D'altra parte, Alice conosce entrambe le parità, ma non sa quale di queste Bob conosce. Siano
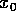 e
e  questi due bit di parità
e sia
questi due bit di parità
e sia  la conoscenza di Bob (cioè Bob conosce
la conoscenza di Bob (cioè Bob conosce 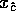 ).
). - Bob dice ad Alice se
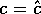 o meno (notiamo che questa è la prima volta che c entra in gioco nel protocollo).
o meno (notiamo che questa è la prima volta che c entra in gioco nel protocollo). - Se
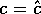 , Alice manda a Bob
, Alice manda a Bob 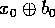 e
e  , nell'ordine prescritto (solo ora entrano in
gioco
, nell'ordine prescritto (solo ora entrano in
gioco 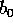 e
e 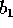 ), altrimenti gli manda
), altrimenti gli manda 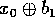 e
e 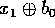 . Da queste informazioni, Bob è in grado di
apprendere il suo
. Da queste informazioni, Bob è in grado di
apprendere il suo 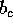 .
.
Notiamo che, poiché Alice non sa se Bob conosce 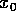 o
o  , non può rendersi conto se egli ha appreso
, non può rendersi conto se egli ha appreso 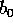 o
o 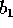 .
D'altra parte, Bob conosce solo
.
D'altra parte, Bob conosce solo 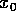 o solo
o solo  , per cui non può apprendere contemporaneamente
, per cui non può apprendere contemporaneamente 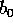 e
e 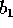 . Quindi, l'OT è
realizzato. Per garantire la sicurezza dell'OT, possiamo enunciare il seguente teorema:
. Quindi, l'OT è
realizzato. Per garantire la sicurezza dell'OT, possiamo enunciare il seguente teorema:
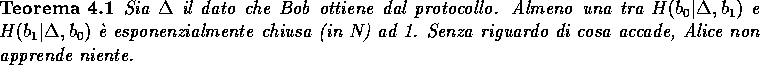
In pratica questo significa che Bob o conosce 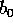 o conosce
o conosce 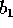 ma non può conoscere entrambi, altrimenti entrambe le entropie varrebbero 0.
Il resto del capitolo costituisce la dimostrazione di questo teorema.
ma non può conoscere entrambi, altrimenti entrambe le entropie varrebbero 0.
Il resto del capitolo costituisce la dimostrazione di questo teorema.



Successivo: Ulteriori considerazioni sul protocollo
Su: Oblivious Transfer
Precedente: Oblivious Transfer
Aniello Castiglione e Gerardo Maiorano < anicas,germai@zoo.diaedu.unisa.it >
![]() e
e ![]() ). Siano, ora,
). Siano, ora, ![]() e
e ![]() i bit di Alice e sia c la scelta di Bob (cioè Bob vuole ottenere
i bit di Alice e sia c la scelta di Bob (cioè Bob vuole ottenere ![]() ).
Il protocollo per l'OT è il seguente:
).
Il protocollo per l'OT è il seguente:
![]() o
o ![]() , non può rendersi conto se egli ha appreso
, non può rendersi conto se egli ha appreso ![]() o
o ![]() .
D'altra parte, Bob conosce solo
.
D'altra parte, Bob conosce solo ![]() o solo
o solo ![]() , per cui non può apprendere contemporaneamente
, per cui non può apprendere contemporaneamente ![]() e
e ![]() . Quindi, l'OT è
realizzato. Per garantire la sicurezza dell'OT, possiamo enunciare il seguente teorema:
. Quindi, l'OT è
realizzato. Per garantire la sicurezza dell'OT, possiamo enunciare il seguente teorema:
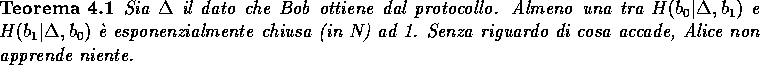
![]() o conosce
o conosce ![]() ma non può conoscere entrambi, altrimenti entrambe le entropie varrebbero 0.
Il resto del capitolo costituisce la dimostrazione di questo teorema.
ma non può conoscere entrambi, altrimenti entrambe le entropie varrebbero 0.
Il resto del capitolo costituisce la dimostrazione di questo teorema.