


Successivo: Analisi dell'informazione di Bob
Su: Bit commitment
Precedente: Bit commitment
Forniamo, innanzitutto, alcuni formalismi matematici che ci saranno utili nel seguito. Sia 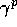 la variabile casuale che assume
il valore binario 0 con probabilità p e 1 con probabilità 1-p. Se p=1/2 ometteremo l'apice 1/2. Denotiamo con
la variabile casuale che assume
il valore binario 0 con probabilità p e 1 con probabilità 1-p. Se p=1/2 ometteremo l'apice 1/2. Denotiamo con 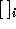 la funzione selezione tale che
la funzione selezione tale che 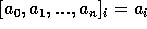 .
Sia
.
Sia 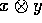 il prodotto scalare booleano, cioè se
il prodotto scalare booleano, cioè se 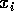 ,
, 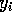 sono gli i-esimi bit di x e y, avremo:
sono gli i-esimi bit di x e y, avremo:
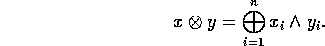
Sia, infine, 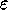 un limite superiore alla percentuale d'errore del canale quantistico, cioè la probabilità che un fotone
un limite superiore alla percentuale d'errore del canale quantistico, cioè la probabilità che un fotone
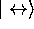 polarizzato venga rilevato come
polarizzato venga rilevato come  . Desciviamo, inizialmente, il protocollo commit(x) utilizzato
da Alice per impegnarsi ad un bit x nei confronti di Bob.
. Desciviamo, inizialmente, il protocollo commit(x) utilizzato
da Alice per impegnarsi ad un bit x nei confronti di Bob.
commit(x)
- Bob sceglie una matrice booleana M come una matrice generatrice di un codice binario lineare (n,k,d) C, tale che
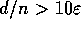 e k/n = 0.52 e la annuncia ad Alice.
e k/n = 0.52 e la annuncia ad Alice. - Alice sceglie una stringa casuale a n bit
 e la annuncia a Bob.
e la annuncia a Bob. - Alice sceglie una parola codice casuale a n bit
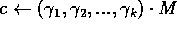 da C, tale che
da C, tale che  .
. - Per i=1,...,n
- Alice sceglie un bit casuale
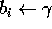 e definisce la sua base di trasmissione
e definisce la sua base di trasmissione 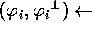
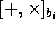 (cioè se
(cioè se 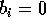 la base dell'i-esimo fotone mandato sarà rettilinea; se
la base dell'i-esimo fotone mandato sarà rettilinea; se 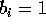 sarà diagonale
questo per la funzione di selezione).
sarà diagonale
questo per la funzione di selezione). - Alice manda a Bob un fotone
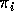 con polarizzazione
con polarizzazione 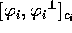 (ciò significa che, supposto
(ciò significa che, supposto
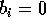 , se,
, se,  , allora
, allora 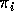 sarà rettilineo orizzontale, altrimenti se
sarà rettilineo orizzontale, altrimenti se  sarà rettilineo verticale. Se, invece,
sarà rettilineo verticale. Se, invece,  , sarà diagonale a 45 gradi se
, sarà diagonale a 45 gradi se  e diagonale a 135 gradi se
e diagonale a 135 gradi se  .
.
- Per i=1,...,n
Siano c', b e b' i vettori 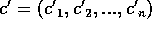 ,
, 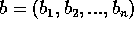 e
e 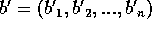 .
Alice tiene x, c e b segreti finché (e se) le rivelazioni hanno luogo, mentre Bob tiene c' e b' segreti per sempre.
Notiamo anche che il vettore casuale r è fornito a Bob in chiaro, mentre la parola codice casuale c è mandata attraverso il canale quantistico,
codificandola mediante fotoni polarizzati nelle basi scelte casualmente. Poichè Bob non conosce in quali basi i fotoni sono polarizzati, egli li misura
in basi scelte casualmente. Quando sceglie la base corretta (
.
Alice tiene x, c e b segreti finché (e se) le rivelazioni hanno luogo, mentre Bob tiene c' e b' segreti per sempre.
Notiamo anche che il vettore casuale r è fornito a Bob in chiaro, mentre la parola codice casuale c è mandata attraverso il canale quantistico,
codificandola mediante fotoni polarizzati nelle basi scelte casualmente. Poichè Bob non conosce in quali basi i fotoni sono polarizzati, egli li misura
in basi scelte casualmente. Quando sceglie la base corretta ( 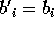 ), il che avviene con probabilità 1/2, egli ottiene il corretto bit
(
), il che avviene con probabilità 1/2, egli ottiene il corretto bit
( 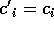 ), eccetto con probabilità d'errore al più
), eccetto con probabilità d'errore al più 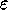 . Dall'altro lato, quando sceglie la base errata (
. Dall'altro lato, quando sceglie la base errata ( 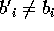 ),
il suo bit non è correlato con il bit di Alice, tuttavia,
),
il suo bit non è correlato con il bit di Alice, tuttavia, 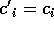 ugualmente con probabilità 1/2 (in quanto anche se sbaglia la base,
comunque puó ottenere 0 o 1 con probabilità 1/2, per il principio di indeterminazione). Quindi, la lettura di Bob della parola c di Alice è
corretta su approssimativamente il
ugualmente con probabilità 1/2 (in quanto anche se sbaglia la base,
comunque puó ottenere 0 o 1 con probabilità 1/2, per il principio di indeterminazione). Quindi, la lettura di Bob della parola c di Alice è
corretta su approssimativamente il  dei bit (
dei bit ( 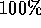 nel primo caso e
nel primo caso e 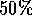 nel secondo, per cui in media
nel secondo, per cui in media  ). Un ingannevole Bob, come sappiamo,
potrebbe ottenere circa l'
). Un ingannevole Bob, come sappiamo,
potrebbe ottenere circa l'  dei bit correttamente, utilizzando la base Breidbart, e dimostreremo che questo è il meglio che possa fare.
Notiamo, inoltre, che il codice lineare C è scelto in maniera tale che ci sono esponenzialmente molte parole codice intorno a quella ricevuta da Bob,
c', che sono alla stessa distanza di Hamming da quella trasmessa da Alice c. Ciò per evitare che Bob possa risalire più facilmente alla parola c
di Alice e, quindi, ad x. Per questo motivo, la distanza minima tra parole codice non dovrebbe essere grande (perché, altrimenti, le parole codice
alla stessa distanza da c sarebbero poche da trovare). Il risultato precedente è indispensabile per un corretto protocollo, perché come vedremo
nel seguito (teorema 5.4), essendo r scelta casualmente, la conoscenza di r e c' danno a Bob un ammontare di attesa informazione di Shannon esponenzialmente
piccola su
dei bit correttamente, utilizzando la base Breidbart, e dimostreremo che questo è il meglio che possa fare.
Notiamo, inoltre, che il codice lineare C è scelto in maniera tale che ci sono esponenzialmente molte parole codice intorno a quella ricevuta da Bob,
c', che sono alla stessa distanza di Hamming da quella trasmessa da Alice c. Ciò per evitare che Bob possa risalire più facilmente alla parola c
di Alice e, quindi, ad x. Per questo motivo, la distanza minima tra parole codice non dovrebbe essere grande (perché, altrimenti, le parole codice
alla stessa distanza da c sarebbero poche da trovare). Il risultato precedente è indispensabile per un corretto protocollo, perché come vedremo
nel seguito (teorema 5.4), essendo r scelta casualmente, la conoscenza di r e c' danno a Bob un ammontare di attesa informazione di Shannon esponenzialmente
piccola su  . Dall'altro canto , tuttavia, la distanza minima tra parole codice deve essere sufficientemente grande da prevenire Alice nel
trovare due differenti parole codice,
. Dall'altro canto , tuttavia, la distanza minima tra parole codice deve essere sufficientemente grande da prevenire Alice nel
trovare due differenti parole codice,  e
e 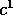 (insieme con basi mandate possibilmente false) in maniera tale da poter affermare di aver mandato
l'una anziché l'altra, così che Bob sarebbe disposto a dare la colpa agli errori di trasmissione per la differenza tra la parola codice mandata
da Alice e la sua misura c' (Teorema 5.7). Di conseguenza è necessario bilanciare queste due esigenze, nella scelta della distanza minima del codice C,
per prevenire Alice e Bob dall'ingannare, da cui i misteriosi parametri
(insieme con basi mandate possibilmente false) in maniera tale da poter affermare di aver mandato
l'una anziché l'altra, così che Bob sarebbe disposto a dare la colpa agli errori di trasmissione per la differenza tra la parola codice mandata
da Alice e la sua misura c' (Teorema 5.7). Di conseguenza è necessario bilanciare queste due esigenze, nella scelta della distanza minima del codice C,
per prevenire Alice e Bob dall'ingannare, da cui i misteriosi parametri 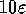 e 0.52 nel protocollo commit(x).
A questo punto, se Alice decide di rivelare il suo impegno x, affinché Bob possa apprendere il corretto valore di x e provare che Alice aveva in mente
proprio quel bit, è necessario che entrambi intraprendano il seguente protocollo:
unveil((c,b,x),(c',b'))
e 0.52 nel protocollo commit(x).
A questo punto, se Alice decide di rivelare il suo impegno x, affinché Bob possa apprendere il corretto valore di x e provare che Alice aveva in mente
proprio quel bit, è necessario che entrambi intraprendano il seguente protocollo:
unveil((c,b,x),(c',b'))
- Alice rivela c,b e x a Bob.
- Bob pone

- if (
 ), (
), (  ) e (c è una parola codice)
) e (c è una parola codice)
then Bob dà in output accettato
else Bob dà in output rifiutato
In effetti, i parametri che Alice rivela al passo 1 potrebbero anche non essere quelli reali. Tuttavia vedremo che la sicurezza del protocollo è
garantita dal valore 1.4 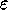 .
.



Successivo: Analisi dell'informazione di Bob
Su: Bit commitment
Precedente: Bit commitment
Aniello Castiglione e Gerardo Maiorano < anicas,germai@zoo.diaedu.unisa.it >
![]() la variabile casuale che assume
il valore binario 0 con probabilità p e 1 con probabilità 1-p. Se p=1/2 ometteremo l'apice 1/2. Denotiamo con
la variabile casuale che assume
il valore binario 0 con probabilità p e 1 con probabilità 1-p. Se p=1/2 ometteremo l'apice 1/2. Denotiamo con ![]() la funzione selezione tale che
la funzione selezione tale che ![]() .
Sia
.
Sia ![]() il prodotto scalare booleano, cioè se
il prodotto scalare booleano, cioè se ![]() ,
, ![]() sono gli i-esimi bit di x e y, avremo:
sono gli i-esimi bit di x e y, avremo:
![]()
![]() un limite superiore alla percentuale d'errore del canale quantistico, cioè la probabilità che un fotone
un limite superiore alla percentuale d'errore del canale quantistico, cioè la probabilità che un fotone
![]() polarizzato venga rilevato come
polarizzato venga rilevato come ![]() . Desciviamo, inizialmente, il protocollo commit(x) utilizzato
da Alice per impegnarsi ad un bit x nei confronti di Bob.
. Desciviamo, inizialmente, il protocollo commit(x) utilizzato
da Alice per impegnarsi ad un bit x nei confronti di Bob.

![]() e quindi, la base è rettilinea
e quindi, la base è rettilinea ![]() orizzontale e
orizzontale e ![]() verticale,
per cui
verticale,
per cui ![]() varrà 0 o 1 a seconda dell'esito della misura).
varrà 0 o 1 a seconda dell'esito della misura).
