Sia x il messaggio in chiaro e sia y la codifica di x ottenuta usando la chiave k. Come visto nella Sezione 3.3, y è ottenuto facendo la somma carattere per carattere tra x e k modulo 26.
Per attaccare questo crittosistema si ipotizza che il testo in chiaro sia scritto in un linguaggio naturale; non si conosce né la chiave k, né la sua lunghezza m . Ancora una volta si sfruttano le proprietá statistiche del messaggio originario. Il primo problema è sapere la lunghezza della chiave.
Kasiski lo ha risolto fornendo un metodo che va alla ricerca di alcune regolaritá che si
ripetono all'interno del testo cifrato. Il test di Kasiski
é basato sull'osservazione che due segmenti identici del testo in chiaro vengono cifrati allo
stesso modo solo se la porzione di chiave atta a cifrarli è la stessa per entrambi. Di contro,
se troviamo due segmenti identici del testo cifrato, ciascuno di lunghezza almeno tre, allora ci
sono buone probabilitá che essi corrispondano a pezzi identici del testo in chiaro.
Il test di Kasiski cerca le coppie di segmenti identici nel testo cifrato
di lunghezza almeno tre e memorizza la distanza tra le posizioni iniziali dei due segmenti. Se si
ottengono le distanze ![]() ,
, ![]() ,
, ![]() , allora si puó dedurre che m (lunghezza della
chiave) divida il gcd dei
, allora si puó dedurre che m (lunghezza della
chiave) divida il gcd dei ![]() . Il limite di questo metodo è che fornisce solo la probabile
lunghezza della chiave e non il suo valore.
. Il limite di questo metodo è che fornisce solo la probabile
lunghezza della chiave e non il suo valore.
Un secondo metodo che puó anche essere accoppiato al test di Kasiski, si basa sul calcolo delle statistiche relative al testo cifrato. Esso consiste in due passi: nel primo viene calcolata la lunghezza della chiave, nel secondo il suo valore.
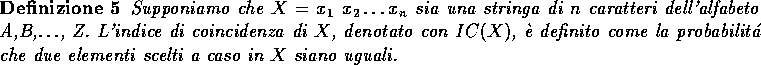
Ricordiamo, a questo punto, che la probabilitá si puó calcolare come
![]()
e osserviamo che, data una stringa ![]() , il numero di modi di scegliere
due caratteri è
, il numero di modi di scegliere
due caratteri è ![]() ; se indichiamo con
; se indichiamo con ![]() le frequenze dei caratteri da A a Z in X allora il numero di modi di scegliere due caratteri in X entrambi uguali
ad A è
le frequenze dei caratteri da A a Z in X allora il numero di modi di scegliere due caratteri in X entrambi uguali
ad A è ![]() , entrambi uguali a B è
, entrambi uguali a B è ![]() , da cui otteniamo che il numero di casi favorevoli è :
, da cui otteniamo che il numero di casi favorevoli è :
![]() +
+ ![]() +
+ ![]() +
+ ![]()
Supponiamo che il messaggio in chiaro X sia in lingua italiana, dal momento
che si conosce la distribuzione tipica dei caratteri in un testo, cioé si sa che la 'E' è la piú probabile , la 'I' è la seconda piú probabile,...etc, si puó calcolare il valore medio di IC(X). Dette ![]() le probabilitá delle occorrenze delle lettere 'A', 'B',
le probabilitá delle occorrenze delle lettere 'A', 'B', ![]() , 'Z', calcolate in base alla Tabella 2, abbiamo che la probabilitá che in un testo scelto a caso vi siano due A è
, 'Z', calcolate in base alla Tabella 2, abbiamo che la probabilitá che in un testo scelto a caso vi siano due A è ![]() , due B
, due B ![]() ,...etc. Allora si ha che :
,...etc. Allora si ha che :
![]()
Se supponiamo che X venga cifrato usando sempre la stessa chiave allora l'indice di coincidenza del messaggio in codice è lo stesso di X perché i vari
caratteri in X sono sostituiti sempre allo stesso modo e quindi le coincidenze nel messaggio in codice sono le stesse del messaggio in chiaro.
Questo ci aiuta perché, se prendendo il messaggio cifrato e calcolandone l'indice di coincidenza, otteniamo un valore vicino a quello del testo in chiaro
che è 0.075 allora possiamo ipotizzare che il testo sia stato cifrato usando sempre la stessa chiave.
Osserviamo peró che in un testo i cui caratteri sono scelti a caso si ha:

Quindi il valor medio dell'indice di coincidenza è :
![]()
che è sufficientemente distante da 0.075; questo ci permette di dire che se l'indice di coincidenza del messaggio in codice è diverso da 0.075 e vicino a 0.038 allora la chiave usata per cifrare il messaggio in chiaro non è la stessa. Pertanto si puó, in questo modo, determinare correttamente la lunghezza della chiave. Detta m la lunghezza della chiave, l'analisi procede come segue:
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
Una volta individuata la lunghezza della chiave potremmo attaccare il crittosistema usufruendo della
sola lunghezza della chiave provando, con la forza bruta, tutte le possibili chiavi.
Se, per esempio, la lunghezza della chiave fosse 7, potremmo provare tutte le ![]() chiavi possibili.
Risulta evidente che una tale soluzione é di fatto impraticabile per cui utilizzeremo una tecnica
statistica che generalizza l'indice di coincidenza a due stringhe.
chiavi possibili.
Risulta evidente che una tale soluzione é di fatto impraticabile per cui utilizzeremo una tecnica
statistica che generalizza l'indice di coincidenza a due stringhe.

Possiamo calcolare il valor medio di MI nel caso in cui conosciamo le distribuzioni di X e Y.
Supponiamo che ![]() e
e ![]() siano due messaggi ottenuti cifrando rispettivamente X ed Y con le chiavi
siano due messaggi ottenuti cifrando rispettivamente X ed Y con le chiavi ![]() e
e ![]() in
in ![]() allora possiamo calcolare
allora possiamo calcolare ![]() calcolando le probabilitá di avere due caratteri uguali.
Avendo, per esempio,
calcolando le probabilitá di avere due caratteri uguali.
Avendo, per esempio, ![]() e
e ![]() , si puó dire che la
probabilitá di avere in
, si puó dire che la
probabilitá di avere in ![]() una A ed in
una A ed in ![]() una A è pari alla
probabilitá di avere Z in X e W in Y, mentre la probabilitá di avere BB è uguale alla probabilitá di avere AX, ...etc.
Se indichiamo con
una A è pari alla
probabilitá di avere Z in X e W in Y, mentre la probabilitá di avere BB è uguale alla probabilitá di avere AX, ...etc.
Se indichiamo con ![]() le probabilitá dei singoli
caratteri allora si ha che in genere la probabilitá di avere AA è:
le probabilitá dei singoli
caratteri allora si ha che in genere la probabilitá di avere AA è:
![]()
quella di avere BB è:
![]()
e cosı via. Ma allora il valor medio è:
dove l'aritmetica è modulo 26.
Osserviamo che dalla (6), il valor medio dell'indice mutuo di coincidenza dipende solo dalla
differenza tra le due chiavi. Infatti, ponendo ![]() otteniamo:
otteniamo:
![]()
Questo risultato ci dice che i possibili indici di coincidenza sono 26. Dato che, preso un certo valore l, si ha:
![]()
si deduce che il valore atteso per l'indice mutuo di coincidenza dipende solo da ![]() e puó assumere solo 14 valori. Tali valori possono essere tabulati in due colonne di cui la prima
rappresenta la differenza tra le due chiavi e la seconda rappresenta il valore atteso dell'indice mutuo
di coincidenza. La Tabella per la lingua italiana è la seguente:
e puó assumere solo 14 valori. Tali valori possono essere tabulati in due colonne di cui la prima
rappresenta la differenza tra le due chiavi e la seconda rappresenta il valore atteso dell'indice mutuo
di coincidenza. La Tabella per la lingua italiana è la seguente:
| shift relativo | valore atteso di MI |
| 0 | 0.075 |
| 1 | 0.033 |
| 2 | 0.034 |
| 3 | 0.034 |
| 4 | 0.047 |
| 5 | 0.027 |
| 6 | 0.032 |
| 7 | 0.026 |
| 8 | 0.027 |
| 9 | 0.023 |
| 10 | 0.024 |
| 11 | 0.027 |
| 12 | 0.015 |
| 13 | 0.021 |
- Tabella 3 : Valori attesi di MI -
A questo punto possiamo vedere un esempio di come vengono usati questi valor medi di MI con la lunghezza della chiave pari a 3. Il messaggio cifrato verrá scritto come
|
| | |
|
| | |
|
| | |
|
| | |
|
| |
Se lo shift tra ![]() e
e ![]() è 0, cioè
è 0, cioè ![]() -
- ![]() , allora MI(a,b),
con a prima colonna e b seconda, è vicino al valore atteso 0.075;
se lo shift è diverso da zero, ad esempio è 1, cioè
, allora MI(a,b),
con a prima colonna e b seconda, è vicino al valore atteso 0.075;
se lo shift è diverso da zero, ad esempio è 1, cioè
![]() -
- ![]() , allora MI(a,b'), con
, allora MI(a,b'), con ![]() la colonna
ottenuta da b shiftando tutti i suoi caratteri di una posizione, è vicino al valore atteso 0.075.
Analogamente si procederá con gli altri shift 2, 3,
la colonna
ottenuta da b shiftando tutti i suoi caratteri di una posizione, è vicino al valore atteso 0.075.
Analogamente si procederá con gli altri shift 2, 3, ![]() 25.
Per questi 26 valori ce ne sará uno solo per cui MI sará vicino a 0.075 da cui possiamo ipotizzare
di aver trovato il valore dello shift.
In questo modo è possibile calcolare lo shift relativo tra il primo e il secondo carattere della
chiave, tra il primo e il terzo, e cosı via, ottenendo un sistema di m-1 equazioni in cui
tutte le chiavi sono espresse in funzione della prima,
25.
Per questi 26 valori ce ne sará uno solo per cui MI sará vicino a 0.075 da cui possiamo ipotizzare
di aver trovato il valore dello shift.
In questo modo è possibile calcolare lo shift relativo tra il primo e il secondo carattere della
chiave, tra il primo e il terzo, e cosı via, ottenendo un sistema di m-1 equazioni in cui
tutte le chiavi sono espresse in funzione della prima, ![]() , che è incognita.
, che è incognita.
A questo punto basterá provare
le 26 possibili scelte per ![]() per avere il valore corretto della chiave.
per avere il valore corretto della chiave.
Di seguito presentiamo lo pseudocodice di un algoritmo che realizza i due passi della crittoanalisi appena descritta.
CALCOLO DELL'INDICE DI COINCIDENZA
FUNZ_COINCIDENZA (Y,lung_max)
(1) ![]() lung¯_chiave = 1
lung¯_chiave = 1 ![]() lung_max
lung_max
(2) INIZIALIZZA(FREQ)
(3) ![]() riga= 0
riga= 0 ![]() lung_chiave - 1
lung_chiave - 1
(4) ![]() colonna = riga
colonna = riga ![]() lung_mess step riga
lung_mess step riga
(5) car_to_int = cifrato[colonna] - 65
(6) FREQ[riga,car_to_int] = FREQ[riga,car_to_int] + 1
(7) ![]() riga = 0
riga = 0 ![]() lung_chiave - 1
lung_chiave - 1
(8) ![]() colonna = 0
colonna = 0 ![]() 25
25
(9) lung[riga] = lung[riga] + FREQ[riga,colonna]
(10) INIZIALIZZA(INDICE)
(11) ![]() riga = 0
riga = 0 ![]() lung_chiave - 1
lung_chiave - 1
(12) ![]() colonna = 0
colonna = 0 ![]() 25
25
(13) ![]() FREQ[riga,colonna]
FREQ[riga,colonna] ![]() 2
2
(14) INDICE[lung_chiave,riga] = INDICE[lung_chiave,riga] + ( FREQ[riga,colonna] ![]() (FREQ[riga,colonna] - 1))
(FREQ[riga,colonna] - 1))
(15) INDICE[lung_chiave,riga] = INDICE[lung_chiave,riga] / (lung[riga] ![]() (lung[riga] - 1))
(lung[riga] - 1))
(16) cont = 0
(17) ![]() colonna = 0
colonna = 0 ![]() lung_chiave - 1
lung_chiave - 1
(18) ![]() INDICE[lung_chiave,colonna] - ATTESO
INDICE[lung_chiave,colonna] - ATTESO ![]() ERRORE
ERRORE
(19) cont = cont + 1
(20) ![]() cont = lung_chiave
cont = lung_chiave
(21) min = indice piu' vicino al valore atteso
(22) SCOSTAMENTO[lung_chiave] = min
(23) CALCOLO DEL MINIMO INDICE DI COINCIDENZA TRA GLI SCOSTAMENTI
(24) STAMPA DELLA PROBABILE LUNGHEZZA DELLA CHIAVE
(25) INIZIALIZZA(vettore[,])
La funzione FUNZ_COINCIDENZA calcola l'indice di coincidenza per tutte le possibili sottostringhe in cui puó essere suddiviso il messaggio cifrato Y in base alla lunghezza della chiave, che puó assumere al piú lunghezza lung_max. Ottenuti tutti i possibili valori si calcola il piú piccolo scostamento che si ha tra il valore atteso e quelli risultanti. Questi scostamenti sono memorizzati in un vettore, in modo tale che ad ogni valore della lunghezza della chiave corrisponda uno scostamento. Lo scostamento piú piccolo corrisponde al valore piú probabile per la lunghezza della chiave.
Nel dettaglio, le linee da (3) a (6) calcolano le frequenze dei caratteri per ogni sottostringa ottenuta dal messaggio cifrato, conservando questi valori in un vettore bidimensionale FREQ. Ad ogni passo del ciclo di linea (1) questo vettore viene inizializzato a 0 (linea (2)), in modo tale che le frequenze siano sempre relative al singolo valore della lunghezza della chiave.
Le linee da (7) a (9) calcolano la lunghezza delle sottostringhe, che comunque non possono differire per piú di un elemento.
La linea (10) inizializza il vettore che contiene i valori degli indici di coincidenza calcolati per i singoli valori della lunghezza della chiave. Essi ovviamente cambiano ad ogni passo del ciclo in linea (1), da cui la necessitá di inizializzare.
Nelle linee da (11) a (15) è calcolato effettivamente il valore degli indici di coincidenza, realizzando la formula 4.
A questo punto si verifica che tutti i valori degli indici di coincidenza ottenuti, si avvicinino con buona approssimazione al valore ATTESO; se ció accade, cioé la variabile cont assume lo stesso valore di lung_chiave allora si passa al calcolo dello scostamento piú piccolo, memorizzando tale valore in un vettore chiamato SCOSTAMENTO.
Alla fine, quando tutti i valori possibili di lung_chiave sono stati analizzati, si calcola il minimo scostamento e di conseguenza la probabile lunghezza della chiave.
CALCOLO DELL'INDICE MUTUO DI COINCIDENZA
FUNZ_MUTUO_INDICE(lung_chiave)
(1) ![]() riga= 0
riga= 0 ![]() lung_chiave - 1
lung_chiave - 1
(2) ![]() colonna = riga
colonna = riga ![]() lung_mess step riga
lung_mess step riga
(3) car_to_int = cifrato[colonna] - 65
(4) FREQ[riga,car_to_int] = FREQ[riga,car_to_int] + 1
(5) ![]() riga = 0
riga = 0 ![]() lung_chiave - 1
lung_chiave - 1
(6) ![]() colonna = 0
colonna = 0 ![]() 25
25
(7) lung[riga] = lung[riga] + FREQ[riga,colonna]
(8) min = 1
(9) ![]() riga = 1
riga = 1 ![]() lung_chiave - 1
lung_chiave - 1
(10) ![]() colonna = riga + 1
colonna = riga + 1 ![]() lung_chiave
lung_chiave
(11) ![]() shift = 0
shift = 0 ![]() 25
25
(12) tmp = 0
(13) ![]() somma = 0
somma = 0 ![]() 25
25
(14) ![]() FRĒQ[riga,somma]
FRĒQ[riga,somma] ![]() 0 AND FREQ[colonna,(somma + shift) mod 26]
0 AND FREQ[colonna,(somma + shift) mod 26] ![]() 0
0
(15) tmp = tmp + (FREQ[riga,somma] ![]() FREQ[colonna,(somma + shift) mod 26])
FREQ[colonna,(somma + shift) mod 26])
(16) MIC[riga,colonna,shift] = tmp / (lung[riga] ![]() lung[colonna])
lung[colonna])
(17) calcolo del MIC che si avvicina maggiormente al valore atteso
(18) COSTRUZIONE DEL SISTEMA PER IL CALCOLO EFFETTIVO DELLA CHIAVE
La FUNZ_MUTUO_INDICE prende in input dalla FUNZ_COINCIDENZA la probabile lunghezza della chiave e restituisce il valore delle possibili chiavi.
Nel dettaglio, dalla linea (1) alla (7) si calcolano le frequenze dei caratteri che compaiono nelle lung_chiave sottostringhe in cui il messaggio cifrato viene suddiviso e le relative lunghezze.
Dalla linea (9) alla (16) viene implementata la formula 6. Nella linea (17) il programma calcola il minimo scarto tra il valore ATTESO e quello dell'indice mutuo di coincidenza.
Nella linea (18), infine, viene risolro il sistema di equazioni lineari che calcola il valore della
chiave in funzione di ![]() .
.

| i | j | Valore di MI |
| 1 | 2 | .0325 .0415 .0422 .0436 .0385 .0444 .0388 .0390 .0347 |
.0350 .0404 .0315 .0419 .0398 .0370 .0380  .0314 .0314 | ||
| .0346 .0356 .0436 .0269 .0327 .0298 .0381 .0371 | ||
| 1 | 3 | .0326 .0341 .0345 .0365 .0245 .0367 .0284 .0393 .0394 |
| .0373 .0358 .0432 .0439 .0399 .0382 .0363 .0334 .0315 | ||
| .0355 .0449 .0384 .0518 .0403 .0313 .0370 | ||
| 1 | 4 | .0380 .0407 .0370 .0381 .0295 .0330 .0415 .0361 .0423 |
| .0411 .0330 .0411 | ||
| .0321 .0316 .0397 .0355 .0354 .0423 .0390 .0403 | ||
| 1 | 5 | .0401 .0393 .0379 .0353 .0345 .0273 .0357 .0461 .0371 |
| .0439 .0420 .0288 .0412 | ||
| .0328 .0387 .0311 .0403 .0368 .0348 .0370 .0340 | ||
| 2 | 3 | .0361 .0328 .0311 .0389 .0334 .0533 .0355 .0390 .0286 |
| | ||
| .0428 .0382 .0446 .0380 .0463 .0358 .0395 .0260 | ||
| 2 | 4 | .0465 .0302 .0369 .0320 .0391 .0410 .0361 .0488 .0354 |
| .0447 .0351 .0440 .0297 .0429 .0318 .0309 .0336 .0327 | ||
| .0442 .0347 .0362 .0328 | ||
| 2 | 5 | .0355 .0419 .0339 .0436 .0320 .0408 .0423 .0371 .0470 |
| .0334 .0434 .0374 .0414 .0295 .0400 .0296 .0317 .0375 | ||
| .0328 .0434 .0355 .0322 .0314 | ||
| 3 | 4 | .0443 .0393 .0421 .0358 .0426 .0318 .0269 .0392 .0318 |
| .0378 .0321 .0363 .0372 | ||
| .0364 .0391 .0324 .0373 .0358 .0315 .0419 .0360 | ||
| 3 | 5 | .0353 .0453 .0415 .0367 .0310 .0374 .0296 .0307 .0446 |
| .0303 .0350 .0321 .0321 .0376 | ||
| .0470 .0397 .0478 .0344 .0388 .0369 .0329 .0399 | ||
| 4 | 5 | .0382 |
| .0336 .0420 .0351 .0427 .0329 .0388 .0361 .0427 .0327 | ||
| .0366 .0317 .0326 .0402 .0367 .0450 .0345 .0319 |
- Tabella 4 -