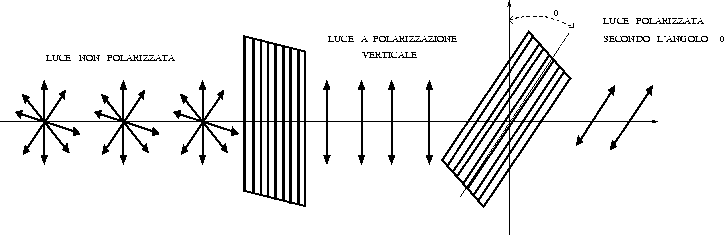
Figura 1: polarizzazione di un raggio di luce
La meccanica quantistica, diversamente dalla meccanica classica, considera un fascio di luce composto da quantità discrete di energia chiamate fotoni. Normalmente un fascio di luce è non polarizzato e tali sono anche i fotoni che lo compongono. Se un fotone o un insieme di essi (raggio luminoso) attraversa un filtro Polaroid (avente proprietà di lasciar passare luce polarizzata solo nella direzione del suo asse), otterremo un fotone polarizzato nella stessa direzione dell'asse del filtro (vedi Figura 1).

Figura 1: polarizzazione di un raggio di luce
Nel seguito utilizzeremo raggi luminosi composti approssimativamente da un solo fotone polarizzato. Un fotone può assumere una qualsiasi polarizzazione, ma per i nostri scopi utilizziamo solo fotoni polarizzati a 0, 45, 90, 135 gradi.
Il canale quantistico è composto da :
Per misurare la polarizzazione di un fotone è possibile usare un cristallo di calcite che invia i fotoni a seconda della loro polarizzazione lungo una delle due possibili direzioni (vedi Figura 2). Quando un fotone incontra un cristallo di calcite si può comportare in due modi, a secondo della sua polarizzazione rispetto al cristallo:
Se, entrando nel cristallo il fotone è già polarizzato in una di queste due direzioni, non subisce modifiche di polarizzazione, ma viene avviato in modo deterministico lungo il cammino diretto o lungo quello traslato. Se invece nel cristallo entra un fotone polarizzato secondo qualche direzione intermedia, esso può seguire, a seconda dei casi, l'uno o l'altro dei due cammini e quindi venire opportunamente ripolarizzato, perdendo la polarizzazione d'origine. Un comportamento del tutto casuale si ha quando la polarizzazione è intermedia fra queste due direzioni, cioè a 45 o 135 gradi: in questo caso la probabilità che il fotone segua l'uno o l'altro cammino è la stessa. In tal modo si perde la memoria della polarizzazione originaria, sulla quale il fotone non rivela nulla.
Supponiamo che un determinato individuo sia informato in anticipo che un certo fotone è polarizzato secondo una delle due direzioni ``rettilinee'', verticale o orizzontale, ma che non sappia quale sia la polarizzazione specifica. Può stabilire con sicurezza questa direzione inviando il fotone in un dispositivo consistente in un cristallo di calcite orientato verticalmente e due rilevatori, capaci di registrare i fotoni. Questo dispositivo non consente di distinguere fotoni la cui direzione di polarizzazione sia 45 o 135 gradi, che però possono essere identificati con sicurezza mediante un identico dispositivo ruotato di 45 gradi rispetto all'orientazione originale. Ovviamente l'apparecchio così ruotato, a sua volta, non può distinguere i fotoni verticali da quelli orizzontali.
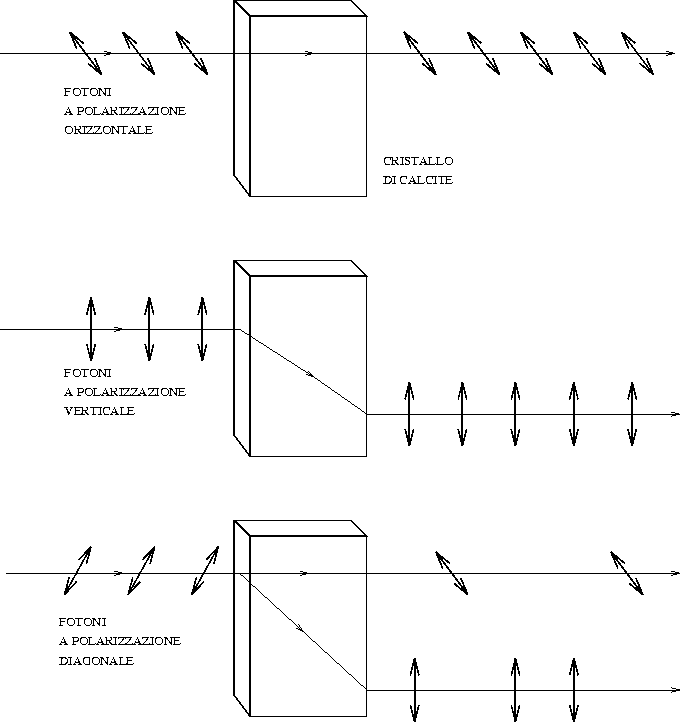
Figura 2: cristallo di calcite attraversato da fotoni
Formalmente la meccanica quantistica rappresenta lo stato interno di un sistema quantistico (ad esempio la polarizzazione di un fotone) come un vettore di lunghezza unitaria in uno spazio lineare sul campo dei numeri complessi, lo spazio di Hilbert. Le dimensioni di tale spazio dipendono dal sistema quantistico ed ogni misura fisica che può essere effettuata sul sistema corrisponde alla risoluzione del suo spazio di Hilbert in sottospazi ortogonali, uno per ogni possibile esito della misura.
Nel nostro caso, lo spazio di Hilbert per un singolo fotone polarizzato è 2-dimensionale, così che
lo stato di un fotone può essere completamente descritto come una combinazione lineare dei due vettori ![]() e
e ![]() , rappresentanti rispettivamente le polarizzazioni orizzontale e verticale. In particolare un fotone
polarizzato ad un angolo
, rappresentanti rispettivamente le polarizzazioni orizzontale e verticale. In particolare un fotone
polarizzato ad un angolo ![]() con l'orizzontale è descritto dallo stato del vettore (
con l'orizzontale è descritto dallo stato del vettore ( ![]() ,
, ![]() ).
I due vettori ortogonali
).
I due vettori ortogonali ![]() e
e ![]() costituiscono la base rettilinea e semplificano la risoluzione dello spazio di
Hilbert a due dimensioni in due sottospazi ortogonali ad una dimensione. In generale ogni coppia di stati di polarizzazione
ortonormali e linearmente indipendenti tra loro, attraverso una combinazione lineare dei quali è possibile esprimere
la polarizzazione di ogni fotone, sarà riferita come una base. Una base alternativa per lo spazio di Hilbert è,
quella diagonale, determinata dai vettori
costituiscono la base rettilinea e semplificano la risoluzione dello spazio di
Hilbert a due dimensioni in due sottospazi ortogonali ad una dimensione. In generale ogni coppia di stati di polarizzazione
ortonormali e linearmente indipendenti tra loro, attraverso una combinazione lineare dei quali è possibile esprimere
la polarizzazione di ogni fotone, sarà riferita come una base. Una base alternativa per lo spazio di Hilbert è,
quella diagonale, determinata dai vettori ![]() e
e ![]() dove
dove ![]() .
In questa base
.
In questa base ![]() rappresenta un fotone a 45 gradi e
rappresenta un fotone a 45 gradi e ![]() un fotone a 135 gradi. Wiesner definisce due basi (quali quella
rettilinea e quella diagonale) essere coniugate se ogni vettore di una base ha una proiezione di uguale lunghezza su tutti i
vettori dell'altra base. Ciò significa che un sistema preparato in uno
stato specifico di una base si comporterà in maniera interamente randomizzata e perderà tutta l'informazione memorizzata
in esso quando sarà soggetto a misure corrispondenti ad una base coniugata alla sua. A causa della natura complessa dei suoi
coefficienti, lo spazio di Hilbert 2-dimensionale ammette anche una terza base coniugata ad entrambe le basi rettilinea e diagonale
ed è quella circolare, data dai vettori
un fotone a 135 gradi. Wiesner definisce due basi (quali quella
rettilinea e quella diagonale) essere coniugate se ogni vettore di una base ha una proiezione di uguale lunghezza su tutti i
vettori dell'altra base. Ciò significa che un sistema preparato in uno
stato specifico di una base si comporterà in maniera interamente randomizzata e perderà tutta l'informazione memorizzata
in esso quando sarà soggetto a misure corrispondenti ad una base coniugata alla sua. A causa della natura complessa dei suoi
coefficienti, lo spazio di Hilbert 2-dimensionale ammette anche una terza base coniugata ad entrambe le basi rettilinea e diagonale
ed è quella circolare, data dai vettori ![]() (
( ![]() ,
, ![]() i) e
i) e ![]() (
( ![]() i,
i, ![]() ) dove
) dove ![]() .
Queste basi sono dette anche basi canoniche e nel seguito saranno sufficienti solo quella rettilinea e quella diagonale per i nostri scopi.
Inoltre ci sarà utile per le misurazioni anche un'altra base, detta base Breidbart, la quale è angolata a 22.5 gradi con
l'orizzontale, esattamente a metà tra la base rettilinea e quella diagonale e, quindi, dalla definizione, non coniugata alle precedenti.
.
Queste basi sono dette anche basi canoniche e nel seguito saranno sufficienti solo quella rettilinea e quella diagonale per i nostri scopi.
Inoltre ci sarà utile per le misurazioni anche un'altra base, detta base Breidbart, la quale è angolata a 22.5 gradi con
l'orizzontale, esattamente a metà tra la base rettilinea e quella diagonale e, quindi, dalla definizione, non coniugata alle precedenti.
In alcuni casi, utilizzeremo la notazione di Dirac per denotare lo stato di un fotone. Per stato di un fotone si intende l'insieme di
tutte le caratteristiche descriventi un fotone, quali energia cinetica, velocità, momento, polarizzazione, componenti di spin ed altro ancora.
In particolare, di queste caratteristiche, prenderemo in considerazione solo la polarizzazione e le componenti di spin.
Se ![]() è lo stato di un fotone nello spazio di Hilbert (dato in termini delle sue componenti rispetto a qualche base),
lo denoteremo con
è lo stato di un fotone nello spazio di Hilbert (dato in termini delle sue componenti rispetto a qualche base),
lo denoteremo con ![]() =
= ![]() .
.
![]() denoterà il complesso coniugato trasposto,
mentre
denoterà il complesso coniugato trasposto,
mentre ![]() ,
, ![]() è
il prodotto scalare. Utilizzando tale formalismo la base rettilinea verrà anche denotata con
è
il prodotto scalare. Utilizzando tale formalismo la base rettilinea verrà anche denotata con ![]() ,
,
![]() quella diagonale con
quella diagonale con ![]() ,
, ![]() .
.
Un ulteriore risultato della fisica quantistica indica che quando una misura è effettuata su un fotone nello stato ![]() ,
ogni esito può occorrere con probabilità data dal quadrato della lunghezza della proiezione di
,
ogni esito può occorrere con probabilità data dal quadrato della lunghezza della proiezione di ![]() nel corrispondente
sottospazio. Come risultato della misura, lo stato originale
nel corrispondente
sottospazio. Come risultato della misura, lo stato originale ![]() è cancellato e replicato dal vettore proiezione
(rinormalizzato a lunghezza unitaria) corrispondente all'esito osservato. In altri termini, ciò significa che se un fotone
è cancellato e replicato dal vettore proiezione
(rinormalizzato a lunghezza unitaria) corrispondente all'esito osservato. In altri termini, ciò significa che se un fotone ![]() polarizzato
è soggetto ad una misura di polarizzazione lungo l'asse
polarizzato
è soggetto ad una misura di polarizzazione lungo l'asse ![]() , esso si comporta come un fotone
, esso si comporta come un fotone ![]() -polarizzato con probabilità
-polarizzato con probabilità
![]() (quindi, se
(quindi, se ![]() la probabilità di essere un fotone
la probabilità di essere un fotone ![]() -polarizzato è 1 mentre quella di essere un
fotone
-polarizzato è 1 mentre quella di essere un
fotone ![]() -polarizzato è 0 ) e come un fotone
-polarizzato è 0 ) e come un fotone ![]() -polarizzato con probabilità complementare
-polarizzato con probabilità complementare
![]() (e quindi, se
(e quindi, se ![]() , si comporta come un fotone
, si comporta come un fotone ![]() -polarizzato con probabilità 1 e come un fotone
-polarizzato con probabilità 1 e come un fotone
![]() -polarizzato con probabilità 0).
-polarizzato con probabilità 0).
Infine notiamo che se ![]() e, quindi, se stiamo misurando la polarizzazione
diagonale di un fotone inviato con polarizzazione rettilinea (o viceversa), il risultato sarà totalmente casuale, cioè il fotone si
comporterà con probabilità
e, quindi, se stiamo misurando la polarizzazione
diagonale di un fotone inviato con polarizzazione rettilinea (o viceversa), il risultato sarà totalmente casuale, cioè il fotone si
comporterà con probabilità ![]() come un fotone a polarizzazione orizzontale (diagonale a 45 gradi) e con
probabilità
come un fotone a polarizzazione orizzontale (diagonale a 45 gradi) e con
probabilità ![]() =1/2 come un fotone a polarizzazione verticale (diagonale a 135 gradi). Quindi, tutta l'informazione
memorizzata nel fotone sarà totalmente persa, come avevamo predetto.
=1/2 come un fotone a polarizzazione verticale (diagonale a 135 gradi). Quindi, tutta l'informazione
memorizzata nel fotone sarà totalmente persa, come avevamo predetto.
Da un punto di vista pratico si possono trasmettere bit d'informazione utilizzando fotoni opportunamente polarizzati a 0, 45, 90 o 135 gradi, in modo tale che ogni fotone contenga un bit d'informazione. La polarizzazione del fotone trasmesso sarà determinata dal valore del bit da rappresentare (0, 1) e dalla base di conversione utilizzata (rettilinea, diagonale). Un possibile schema è il seguente :
| R | D | Bit |
| | | 0 |
|
| | 1 |
Quindi un utente che voglia trasmettere il bit 1, sceglie una base per rappresentare quel bit (es. R rettilinea)
e manda sul canale quantistico il fotone rappresentante quel bit, ossia un fotone con polarizzazione ![]() .
Colui che riceve può misurare il fotone e quindi identificare il bit, solo se conosce la base con cui esso è
stato convertito. Se la base di conversione non è nota occorre sceglierla a caso fra R e D ottenendo cosìuna
risposta giusta con probabilità 1/2 e una risposta sbagliata con eguale probabilità.
.
Colui che riceve può misurare il fotone e quindi identificare il bit, solo se conosce la base con cui esso è
stato convertito. Se la base di conversione non è nota occorre sceglierla a caso fra R e D ottenendo cosìuna
risposta giusta con probabilità 1/2 e una risposta sbagliata con eguale probabilità.