


Successivo: Strategie di origliamento
Su: Distribuzione quantistica a chiave
Precedente: Distribuzione quantistica a chiave
Vediamo più in dettaglio come due interlocutori, Alice e Bob, possono effettuare una distribuzione a chiave pubblica
su un canale quantistico. Assumiamo la presenza di un origliatore, Eve. Un bit è rappresentato da un fotone polarizzato
come illustrato in Tabella 1. Facciamo infine l'ipotesi, che ogni impulso contenga esattamente un fotone. Il protocollo è il seguente:
- 1
- Alice sceglie una stringa casuale di bit ed una sequenza casuale di basi di polarizzazione (rettilinea o diagonale)
e manda a Bob una sequenza di fotoni, ognuno rappresentante un bit della stringa, nella base scelta.
- 2
- Bob sceglie casualmente per ogni fotone mandatogli da Alice (e indipendentemente dalle scelte
fatte da Alice, perché queste scelte non sono note a Bob a questo punto del protocollo) se misurare la
polarizzazione rettilinea o diagonale e interpreta ogni risultato come 0 o 1, a seconda dell'esito della corrispondente
misura. Come abbiamo più volte ripetuto, una risposta casuale è prodotta e tutta l'informazione è persa quando
si tenta di misurare la polarizzazione rettilinea di un fotone diagonale o viceversa. CosìBob ottiene
dati significativi solo dal
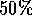 dei fotoni che ha misurato (quelli per i quali ha indovinato la corretta
base di polarizzazione) supponendo che non vi siano state alterazioni dovute ad origliamento.
dei fotoni che ha misurato (quelli per i quali ha indovinato la corretta
base di polarizzazione) supponendo che non vi siano state alterazioni dovute ad origliamento.
- 3
- Bob annuncia pubblicamente le basi con cui ha analizzato i fotoni.
- 4
- Alice comunica a Bob, pubblicamente, se per ciascun fotone che egli ha ricevuto ha eseguito il tipo giusto di
misurazione. Si scartano tutte le posizioni dei bit per le quali Bob ha eseguito un tipo di misurazione sbagliato
o per le quali non è stato rilevato alcun fotone. Ciò può capitare quando un origliatore li ha
intercettati e non ne ha rimandato altri, o quando questi ha effettuato una divisione del raggio e ne ha presi per
sè alcuni, o perché sono stati persi durante il transito, o, infine, perché non sono stati deviati correttamente
verso i fotomoltiplicatori che, di conseguenza, non li hanno rilevati. Infatti osserviamo anche che i fotomoltiplicatori
non hanno un'efficienza quantistica del 100%.
- 5
- Alice e Bob, per verificare se le loro risultanti stringhe di bit sono identiche confrontano
pubblicamente un sottoinsieme casuale dei bit correttamente ricevuti
da Bob, cioè con la base esatta.
Se tutti i fotoni (o quasi) concordano, Alice e Bob possono concludere che la trasmissione quantistica è stata
libera da significativi origliamenti, per cui i rimanenti bit segreti possono costituire
la chiave. Se invece vi è stato un notevole origliamento, la trasmissione è scartata e si riprova con un nuovo
gruppo di fotoni.
Mostriamo ora un esempio reale di ``trasmissione quantistica a chiave pubblica'' fra due ipotetici utenti Alice e Bob
i quali inizialmente non condividono nessuna informazione in comune.
|
1a. | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
|
1b. | D | R | D | R | R | R | R | R | D | D | R | D | D | D | R |
|
1c. |  |  |  |  |  |
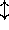 |  |  | 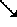 |  |
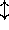 | 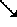 |  |  |  |
|
2a. | R | D | D | R | R | D | D | R | D | R | D | D | D | D | R |
|
2b. | 1 | | 1 | | 1 | 0 | 0 | 0 | | 1 | 1 | 1 | | 0 | 1 |
|
3. | R | | D | | R | D | D | R | | R | D | D | | D | R |
|
4a. | | | OK | | OK | | | OK | | | | OK | | OK | OK |
|
4b. | | | 1 | | 1 | | | 0 | | | | 1 | | 0 | 1 |
|
5a. | | | | | 1 | | | | | | | | | 0 | |
|
5b. | | | | | OK | | | | | | | | | OK | |
|
5c. | | | 1 | | | | | 0 | | | | 1 | | | 1 |
Tabella 2: Esempio di una trasmmissione
Descrizione :
È interessante notare come la probabilità che le risultanti stringhe di Alice e Bob concordino
completamente non può essere resa pari ad 1. Possono, infatti, capitare degli errori, dovuti, ad esempio, a
ripolarizzazioni dei fotoni durante il transito, anche in assenza di origliamento.
Se il numero degli errori capitati è relativamente piccolo essi potrebbero essere corretti mediante l'utilizzo di
un concordato codice a correzione d'errore, generando una sequenza controllata di bit. Questa sequenza può, quindi,
essere inviata a Bob su un canale pubblico. Se il codice ha sufficiente ridondanza, Bob può decodificare univocamente
l'informazione disponibile per recuperare, con alta probabilità la stringa di Alice.
L'elementare controllo di qualità, appena descritto, è dispendioso in quanto una porzione significativa di bit
deve essere sacrificata per fornire un ragionevole margine di sicurezza che i dati dei due interlocutori siano identici,
anche se gli episodi di spionaggio sono stati poco frequenti e hanno causato pochi errori.
Questo inconveniente può essere risolto da un più sottile protocollo di verifica che sfrutta il confronto di parità
di un sottoinsieme casuale di bit scelto pubblicamente.
Il protocollo riconciliativo consta dei seguenti nuovi passi :
- 5'
- Alice e Bob permutano la stringa in base ad una permutazione su cui si sono accordati e, quindi, partizionano le loro
stringhe permutate in blocchi di dimensione k tali che i singoli blocchi contengono, con bassa probabilità, più di un errore
(la dimensione conveniente dei blocchi è 5).
- 6'
- Per ogni blocco, Alice e Bob, confrontano la parità. Blocchi con parità concorde sono ritenuti
momentaneamente corretti (in quanto potrebbero capitare un numero pari di errori) mentre blocchi con parità discorde vengono
sottoposti a ricerca bisettiva, rivelando al limite
 parità supplementari di sottoblocchi, finchè l'errore è
trovato e corretto. Per evitare di fornire troppa informazione ad Eve durante il processo di riconciliazione, Alice e Bob si
accordano anche di scartare l'ultimo bit di ogni blocco o sottoblocco, di cui hanno rilevato la parità.
parità supplementari di sottoblocchi, finchè l'errore è
trovato e corretto. Per evitare di fornire troppa informazione ad Eve durante il processo di riconciliazione, Alice e Bob si
accordano anche di scartare l'ultimo bit di ogni blocco o sottoblocco, di cui hanno rilevato la parità.
- 7'
- Per rimuovere gli errori rimasti (dai blocchi con parità concorde ma con un numero pari di errori),
la permutazione casuale e la rivelazione della parità dei blocchi è ripetuta molte più volte, con dimensione dei blocchi
incrementata, finchè Alice e Bob stimano che al più un piccolo numero di errori rimangono nei dati.
Anche tale approccio, tuttavia, è abbastanza dispendioso. Se la dimensione dei blocchi è scelta cosìche vi siano
l blocchi, la probabilità di non scoprire l'esistenza di tali errori è 1/l e il costo per questa
strategia è di l bit (perché ne perdiamo uno per blocco).
È possibile scegliere una strategia alternativa che risulta essere più efficiente della precedente :
- 5''
- Per ogni iterazione, Alice e Bob confrontano la parità di un sottoinsieme casuale, scelto pubblicamente, delle posizioni
dei bit nelle loro rispettive stringhe. Se le stringhe non sono identiche, allora le parità del sottoinsieme casuale saranno in
disaccordo con probabilità 1/2. Se un disaccordo è trovato, Alice e Bob intraprendono una ricerca bisettiva con lo stesso
criterio (cioè scegliendo un sottoinsieme casuale delle sottostringhe e cosìvia), per trovare e rimuovere gli errori.
Come nel precedente passo, l'ultimo bit di ogni sottoinsieme confrontato è scartato.
Per assicurarsi che le stringhe siano veramente identiche, con una trascurabile probabilità di non scoprire i rimanenti
errori sarà sufficiente attendere 20 accordi consecutivi.
Osserviamo che con questa strategia la probabilità di non scoprire errori dopo l iterazioni è
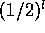 che è molto minore di 1/l, per l grande, e comporta la perdita di ugualmente l bit.
A questo punto del protocollo, Alice e Bob sono in possesso di una stringa che è quasi certamente condivisa, ma solo parzialmente
segreta, in quanto Eve ha potuto apprendere tutti i bit di parità che essi hanno rivelato, oltre ai bit appresi attraverso le sue
misurazioni. Prima di procedere, Alice e Bob devono necessariamente stimare l'intensità dell'origliamento e questo può essere
fatto in base al numero di errori che hanno incontrato e corretto, all'intensità dell'impulso originale ed all'efficienza quantistica
dei rilevatori di Bob. Se osservano un sensibile origliamento, scartano i loro dati e riprovano la trasmissione quantistica.
che è molto minore di 1/l, per l grande, e comporta la perdita di ugualmente l bit.
A questo punto del protocollo, Alice e Bob sono in possesso di una stringa che è quasi certamente condivisa, ma solo parzialmente
segreta, in quanto Eve ha potuto apprendere tutti i bit di parità che essi hanno rivelato, oltre ai bit appresi attraverso le sue
misurazioni. Prima di procedere, Alice e Bob devono necessariamente stimare l'intensità dell'origliamento e questo può essere
fatto in base al numero di errori che hanno incontrato e corretto, all'intensità dell'impulso originale ed all'efficienza quantistica
dei rilevatori di Bob. Se osservano un sensibile origliamento, scartano i loro dati e riprovano la trasmissione quantistica.
Se Alice e Bob ritengono che Eve abbia appreso poca informazione, possono proseguire il protocollo estraendo dalla stringa riconciliata una
sottostringa più piccola ma quasi certamente segreta, applicando la tecnica dell'amplificazione della riservatezza descritta di seguito.
Sia x la stringa riconciliata e n la sua lunghezza. Definiamo innanzitutto un bit deterministico di informazione su x il valore e(x)
di un'arbitraria funzione 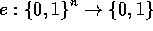 . Bit di parità sono bit deterministici; bit di informazione di Shannon non lo sono.
É possibile dimostrare che se la conoscenza di Eve circa x non è più di l bit deterministici, una funzione hash, scelta pubblicamente
e casualmente da un'appropriata classe di funzioni
. Bit di parità sono bit deterministici; bit di informazione di Shannon non lo sono.
É possibile dimostrare che se la conoscenza di Eve circa x non è più di l bit deterministici, una funzione hash, scelta pubblicamente
e casualmente da un'appropriata classe di funzioni 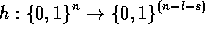 , mapperà x in una stringa h(x) per la quale
l'informazione attesa da Eve è minore di
, mapperà x in una stringa h(x) per la quale
l'informazione attesa da Eve è minore di 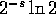 bit, dove s;SPMgt;0 è un arbitrario parametro di sicurezza.
Questa tecnica è applicabile per Alice e Bob perché i bit di parità sono un caso speciale di bit deterministici.
Inoltre per poter scegliere una tale funzione di contrazione, non è neppure necessario che le due parti sappiano quali informazioni
parziali possa avere l'origliatore sull'input. In particolare basta definire ciascun bit dell'output come la parità di un
sottoinsieme indipendente ed aleatorio, concordato pubblicamente, dei bit di input.
bit, dove s;SPMgt;0 è un arbitrario parametro di sicurezza.
Questa tecnica è applicabile per Alice e Bob perché i bit di parità sono un caso speciale di bit deterministici.
Inoltre per poter scegliere una tale funzione di contrazione, non è neppure necessario che le due parti sappiano quali informazioni
parziali possa avere l'origliatore sull'input. In particolare basta definire ciascun bit dell'output come la parità di un
sottoinsieme indipendente ed aleatorio, concordato pubblicamente, dei bit di input.



Successivo: Strategie di origliamento
Su: Distribuzione quantistica a chiave
Precedente: Distribuzione quantistica a chiave
Aniello Castiglione e Gerardo Maiorano < anicas,germai@zoo.diaedu.unisa.it >

![]() . Bit di parità sono bit deterministici; bit di informazione di Shannon non lo sono.
É possibile dimostrare che se la conoscenza di Eve circa x non è più di l bit deterministici, una funzione hash, scelta pubblicamente
e casualmente da un'appropriata classe di funzioni
. Bit di parità sono bit deterministici; bit di informazione di Shannon non lo sono.
É possibile dimostrare che se la conoscenza di Eve circa x non è più di l bit deterministici, una funzione hash, scelta pubblicamente
e casualmente da un'appropriata classe di funzioni ![]() , mapperà x in una stringa h(x) per la quale
l'informazione attesa da Eve è minore di
, mapperà x in una stringa h(x) per la quale
l'informazione attesa da Eve è minore di ![]() bit, dove s;SPMgt;0 è un arbitrario parametro di sicurezza.
Questa tecnica è applicabile per Alice e Bob perché i bit di parità sono un caso speciale di bit deterministici.
Inoltre per poter scegliere una tale funzione di contrazione, non è neppure necessario che le due parti sappiano quali informazioni
parziali possa avere l'origliatore sull'input. In particolare basta definire ciascun bit dell'output come la parità di un
sottoinsieme indipendente ed aleatorio, concordato pubblicamente, dei bit di input.
bit, dove s;SPMgt;0 è un arbitrario parametro di sicurezza.
Questa tecnica è applicabile per Alice e Bob perché i bit di parità sono un caso speciale di bit deterministici.
Inoltre per poter scegliere una tale funzione di contrazione, non è neppure necessario che le due parti sappiano quali informazioni
parziali possa avere l'origliatore sull'input. In particolare basta definire ciascun bit dell'output come la parità di un
sottoinsieme indipendente ed aleatorio, concordato pubblicamente, dei bit di input.