Date due o più sequenze, inizialmente potremmo volere:
- misurarne il grado di similarità;
- determinare la corrispondenza tra residuo e residuo;
- osservarne i pattern di conservazione e variabilità;
- dedurne il rapporto evolutivo.
Se possiamo fare tutto ciò, siamo in una buona posizione per trovare, nelle banche dati, altre sequenze correlate. Una delle più importanti applicazioni è l'annotazione dei genomi, che comporta l'assegnazione di una struttura e di una funzione al maggior numero possibile di geni.
Come possiamo definire una misura quantitativa del grado di similarità di sequenza? Per confrontare i nucleotidi o gli aminoacidi che compaiono in posizioni corrispondenti in due o più sequenze, dobbiamo innanzitutto assegnare tali corrispondenze. L'allineamento di sequenza consiste nell'identificazione delle corrispondenze residuo per residuo. Esso è lo strumento base della bioinformatica.
Qualunque assegnazione di corrispondenze che conservi l'ordine dei residui all'interno delle sequenze è un allineamento. Possono essere introdotti dei gap (interruzioni).
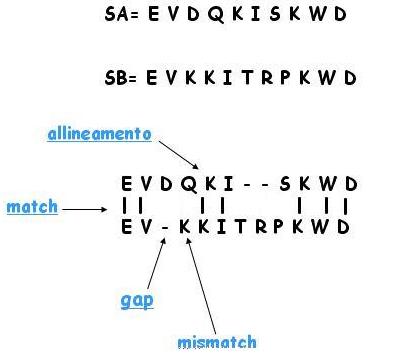
Dobbiamo definire dei criteri, in modo tale che un algoritmo possa permettere di scegliere l'allineamento migliore.

Il semplice algoritmo schematizzato nella figura consente di valutare tutti gli allineamenti tra due sequenze e di calcolarne i rispettivi punteggi, purché le sequenze siano mantenute ininterrotte, cioè siano prive di gap. L’algoritmo comporta lo scorrimento di una sequenza sull’altra e il conteggio del numero di lettere appaiate esattamente. L’allineamento numero 5 risulta migliore, con quattro appaiamenti esatti. Il concetto di miglior allineamento è comunque relativo al criterio usato per valutare la similarità.
Vince l’allineamento con il maggior numero di match.
Fra due sequenze di lunghezza n e m il numero possibile di differenti allineamenti e’ pari a n + m - 1 quando si esclude l’inserimento di gaps.
L’applicazione del semplice algoritmo illustrato nella figura precedente comporta che ad ogni avanzamento della sequenza si dovranno confrontare tutte le lettere appaiate tra le due sequenze. Si può facilmente dimostrare che alla fine si dovranno effettuare un numero di confronti pari al prodotto delle lunghezze delle due sequenze che si vogliono allineare. Infatti ogni lettera della prima sequenza dovrà essere confrontata con ogni lettera dell'altra.
Nel nostro esempio ci sono complessivamente 30 coppie di lettere appaiate: 5 x 6 = 30 (prodotto delle lunghezze delle due sequenze).
E' evidente che l'efficienza di un algoritmo in termini di tempo di esecuzione è determinata dal numero di operazioni necessarie per eseguirlo. Quante più volte è ripetuta una stessa operazione tanto maggiore sarà il tempo richiesto. Nell'esempio illustrato sopra si tratta di un numero di operazioni proporzionale al prodotto delle lunghezze, che si indica con O(nm). Se si suppone che le lunghezze n e m siano dello stesso ordine di grandezza, si userà O(n2).
Come si vedrà più avanti, sono stati realizzati diversi programmi di allineamento basati su algoritmi che richiedono un numero di operazioni O(n2); per esempio quello sviluppato da Needleman e Wunsch oppure quello di Smith e Waterman.
La complessità del problema di allineare sequenze di acidi nucleici e di proteine deriva principalmente dal fatto che deve essere considerata la possibilità che il miglior allineamento comporti l’inserimento di gap nelle sequenze.
I seguenti due allineamenti alternativi sono stati prodotti rispettivamente senza e con la possibilità di inserire gap e appare evidente come inserendo un gap in ciascuna delle due sequenze si passi da 10 a 25 appaiamenti esatti.
Esempio
Senza gap
I P L M T R W D Q E Q E S D F G H K L P I Y T R E W C T R G
| | | | | | | | | |
C H K I P L M T R W D Q Q E S D F G H K L P V I Y T R E W
Con gap
I P L M T R W D Q E Q E S D F G H K L P - I Y T R E W C T R G
| | | | | | | | | | | | | | | | | | | | | | | | |
C H K I P L M T R W D Q - Q E S D F G H K L P V I Y T R E W
L'inserimento di gap comporta principalmente due complicazioni: la prima relativa alla definizione di criteri di similarità e la seconda relativa alla possibilità di disporre di algoritmi adeguati.
Un algoritmo di scorrimento di una sequenza sull’altra è assolutamente inadatto allo scopo perché ci sono troppi modi diversi con cui si può inserire un gap nelle sequenze da allineare. In una sequenza lunga n caratteri è infatti possibile inserire un singolo gap in n-1 posizioni, generando n sequenze diverse. Consentendo un numero peggiore di gap il numero di possibili sequenze aumenta in modo esponenziale. E' quindi essenziale pensare ad algoritmi di allineamento più efficienti.
Intorno al 1970 fu sviluppato un semplice sistema di visualizzazione di allineamenti chiamato dot matrix. Le due sequenze da confrontare sono poste ai margini di una matrice di allineamento: una sequenza è scritta da sinistra a destra in corrispondenza del margine superiore, l’altra dall’alto in basso in corrispondenza del margine sinistro. Quindi ogni casella della matrice fa riferimento a due lettere, una appartenente ad una sequenza e una all’altra. Nel caso più semplice, se le due lettere sono uguali la casella sarà colorata in nero e apparirà come un punto (dot) all’interno della matrice, altrimenti resterà bianca. In questo modo ogni allineamento di una certa lunghezza apparirà come un segmento diagonale e sarà visivamente distinguibile.
Le dot matrix sono molto convenienti per l’immediatezza e l’intuitività con cui spesso riescono a fornire indicazioni utili, tuttavia non esprimono un valore dell’allineamento, ma solo la sua rappresentazione grafica. Esse consentono di individuare e localizzare similarità di sequenza anche in presenza di gap che graficamente appaiono come salti in diagonale, e permettono un facile riconoscimento di regioni ripetute, che appaiono come segmenti diagonali paralleli.
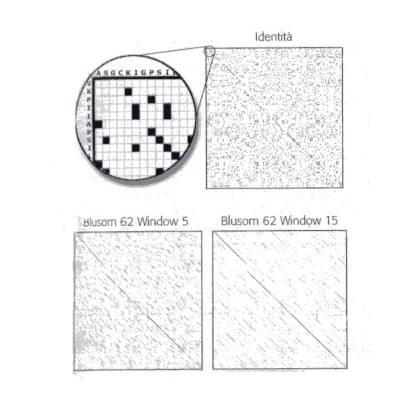
Esempi di dot matrix ottenute con il programma DOTLET. I tre casi raffigurati sono relativi all'allineamento della D-ribulose-5-phosphate-3-epimerase di uomo e di lievito, rappresentate rispettivamente da sinistra a destra e dall'alto in basso in ognuno dei tre riquadri. Il confronto tra le due sequenze è stato fatto adottando criteri diversi. Nel primo caso (in alto) sono marcate solo le caselle che corrispondono all'identità; negli altri due casi è stata adottata la matrice di sostituzione BLOSUM 62 che attribuisce un punteggio positivo, seppure minore a quello dell'identità, anche quando due aminoacidi sono simili. Inoltre, nei due riquadri inferiori, sono riprodotti i punteggi medi delle diagonali che partono da ogni casella e procedono per il numero di posizioni indicato dal parametro window. L'intensità del colore grigio è indicativa del punteggio di ogni diagonale.